# Path之贝塞尔曲线 ### 作者微博: [@GcsSloop](http://weibo.com/GcsSloop) ### [【本系列相关文章】](https://github.com/GcsSloop/AndroidNote/tree/master/CustomView/README.md) 在上一篇文章[Path之基本图形](https://github.com/GcsSloop/AndroidNote/blob/master/CustomView/Advance/%5B05%5DPath_Basic.md)中我们了解了Path的基本使用方法，本次了解Path中非常非常非常重要的内容-贝塞尔曲线。 ****** ## 一.Path常用方法表 > 为了兼容性(_偷懒_) 本表格中去除了在API21(即安卓版本5.0)以上才添加的方法。忍不住吐槽一下，为啥看起来有些顺手就能写的重载方法要等到API21才添加上啊。宝宝此刻内心也是崩溃的。 | 作用 | 相关方法 | 备注 | | ----------- | ---------------------------------------- | ---------------------------------------- | | 移动起点 | moveTo | 移动下一次操作的起点位置 | | 设置终点 | setLastPoint | 重置当前path中最后一个点位置，如果在绘制之前调用，效果和moveTo相同 | | 连接直线 | lineTo | 添加上一个点到当前点之间的直线到Path | | 闭合路径 | close | 连接第一个点连接到最后一个点，形成一个闭合区域 | | 添加内容 | addRect, addRoundRect, addOval, addCircle, addPath, addArc, arcTo | 添加(矩形， 圆角矩形， 椭圆， 圆， 路径， 圆弧) 到当前Path (注意addArc和arcTo的区别) | | 是否为空 | isEmpty | 判断Path是否为空 | | 是否为矩形 | isRect | 判断path是否是一个矩形 | | 替换路径 | set | 用新的路径替换到当前路径所有内容 | | 偏移路径 | offset | 对当前路径之前的操作进行偏移(不会影响之后的操作) | | 贝塞尔曲线 | quadTo, cubicTo | 分别为二次和三次贝塞尔曲线的方法 | | rXxx方法 | rMoveTo, rLineTo, rQuadTo, rCubicTo | **不带r的方法是基于原点的坐标系(偏移量)， rXxx方法是基于当前点坐标系(偏移量)** | | 填充模式 | setFillType, getFillType, isInverseFillType, toggleInverseFillType | 设置,获取,判断和切换填充模式 | | 提示方法 | incReserve | 提示Path还有多少个点等待加入**(这个方法貌似会让Path优化存储结构)** | | 布尔操作(API19) | op | 对两个Path进行布尔运算(即取交集、并集等操作) | | 计算边界 | computeBounds | 计算Path的边界 | | 重置路径 | reset, rewind | 清除Path中的内容<br/> **reset不保留内部数据结构，但会保留FillType.**<br/> **rewind会保留内部的数据结构，但不保留FillType** | | 矩阵操作 | transform | 矩阵变换 | ## 二.Path详解 上一次除了一些常用函数之外，讲解的基本上都是直线，本次需要了解其中的曲线部分,说到曲线，就不得不提大名鼎鼎的贝塞尔曲线。它的发明者是下面这个人(法国数学家PierreBézier)。  ### 贝塞尔曲线能干什么？ 贝塞尔曲线的运用是十分广泛的，可以说**贝塞尔曲线奠定了计算机绘图的基础(_因为它可以将任何复杂的图形用精确的数学语言进行描述_)**，在你不经意间就已经使用过它了。 你会使用Photoshop的话，你可能会注意到里面有一个**钢笔工具**，这个钢笔工具核心就是贝塞尔曲线。 你说你不会PS？ 没关系，你如果看过前面的文章或者用过2D绘图，肯定绘制过圆，圆弧，圆角矩形等这些东西。这里面的圆弧部分全部都是贝塞尔曲线的运用。 #### 贝塞尔曲线作用十分广泛，简单举几个的栗子: > * QQ小红点拖拽效果 * 一些炫酷的下拉刷新控件 * 阅读软件的翻书效果 * 一些平滑的折线图的制作 * 很多炫酷的动画效果 ### 如何轻松入门贝塞尔曲线？ 虽然贝塞尔曲线用途非常广泛，然而目前貌似并没有适合的中文教程，能够搜索出来Android关于贝塞尔曲线的中文文章基本可以分为以下几种： * 科普型(只是让人了解贝塞尔，并没有实质性的内容) * 装逼型(摆出来一大堆公式，引用一堆英文原文) * 基础型(仅仅是讲解贝塞尔曲线的两个函数用法) * 实战型(根据实例讲解其中贝塞尔曲线的运用) 以上几种类型中比较有用的就是基础型和实战型，但两者各有不足，本文会综合两者内容，从零开始学习贝塞尔曲线。 ### 第一步.理解贝塞尔曲线的原理 此处理解贝塞尔曲线并非是学会公式的推导过程(不是推倒(ﾉ*･ω･)ﾉ)，而是要了解贝塞尔曲线是如何生成的。 贝塞尔曲线是用一系列点来控制曲线状态的，我将这些点简单分为两类： | 类型 | 作用 | | ---- | ------------ | | 数据点 | 确定曲线的起始和结束位置 | | 控制点 | 确定曲线的弯曲程度 | > 此处暂时仅作了解概念，接下来就会讲解其中详细的含义。 **一阶曲线原理：** 一阶曲线是没有控制点的，仅有两个数据点(A 和 B)，最终效果一个线段。  > **上图表示的是一阶曲线生成过程中的某一个阶段，动态过程可以参照下图(本文中贝塞尔曲线相关的动态演示图片来自维基百科)。**  > **PS：一阶曲线其实就是前面讲解过的lineTo。** **二阶曲线原理：** 二阶曲线由两个数据点(A 和 C)，一个控制点(B)来描述曲线状态，大致如下：  上图中红色曲线部分就是传说中的二阶贝塞尔曲线，那么这条红色曲线是如何生成的呢？接下来我们就以其中的一个状态分析一下：  连接AB BC，并在AB上取点D，BC上取点E，使其满足条件： <img src="http://chart.googleapis.com/chart?cht=tx&chl=%5Cfrac%7BAD%7D%7BAB%7D%20%3D%20%5Cfrac%7BBE%7D%7BBC%7D" style="border:none;" />  连接DE，取点F，使得: <img src="http://chart.googleapis.com/chart?cht=tx&chl=%5Cfrac%7BAD%7D%7BAB%7D%20%3D%20%5Cfrac%7BBE%7D%7BBC%7D%20%3D%20%5Cfrac%7BDF%7D%7BDE%7D" style="border:none;" /> 这样获取到的点F就是贝塞尔曲线上的一个点，动态过程如下：  > **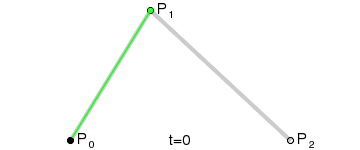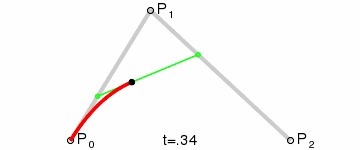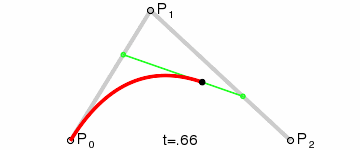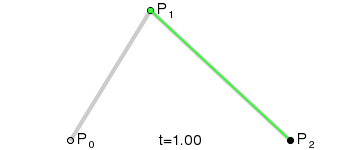PS: 二阶曲线对应的方法是quadTo** **三阶曲线原理：** 三阶曲线由两个数据点(A 和 D)，两个控制点(B 和 C)来描述曲线状态，如下：  三阶曲线计算过程与二阶类似，具体可以见下图动态效果：  > **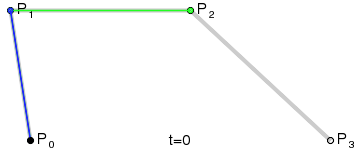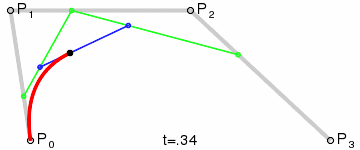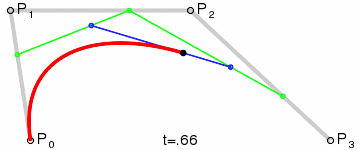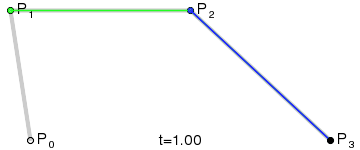PS: 三阶曲线对应的方法是cubicTo** #### [贝塞尔曲线速查表](https://github.com/GcsSloop/AndroidNote/blob/master/QuickChart/Bezier.md) #### 强烈推荐[点击这里](http://bezier.method.ac/)练习贝塞尔曲线，可以加深对贝塞尔曲线的理解程度。 ### 第二步.了解贝塞尔曲线相关函数使用方法 #### 一阶曲线： 一阶曲线是一条线段，非常简单，可以参见上一篇文章[Path之基本操作](https://github.com/GcsSloop/AndroidNote/blob/master/CustomView/Advance/5%5DPath_Basic.md)，此处就不详细讲解了。 #### 二阶曲线： 通过上面对二阶曲线的简单了解，我们知道二阶曲线是由两个数据点，一个控制点构成，接下来我们就用一个实例来演示二阶曲线是如何运用的。 首先，两个数据点是控制贝塞尔曲线开始和结束的位置，比较容易理解，而控制点则是控制贝塞尔的弯曲状态，相对来说比较难以理解，所以本示例重点在于理解贝塞尔曲线弯曲状态与控制点的关系，废话不多说，先上效果图：  > 为了更加容易看出控制点与曲线弯曲程度的关系，上图中绘制出了辅助点和辅助线，从上面的动态图可以看出，贝塞尔曲线在动态变化过程中有类似于橡皮筋一样的弹性效果，因此在制作一些弹性效果的时候很常用。 主要代码如下： ``` java public class Bezier extends View { private Paint mPaint; private int centerX, centerY; private PointF start, end, control; public Bessel1(Context context) { super(context); mPaint = new Paint(); mPaint.setColor(Color.BLACK); mPaint.setStrokeWidth(8); mPaint.setStyle(Paint.Style.STROKE); mPaint.setTextSize(60); start = new PointF(0,0); end = new PointF(0,0); control = new PointF(0,0); } @Override protected void onSizeChanged(int w, int h, int oldw, int oldh) { super.onSizeChanged(w, h, oldw, oldh); centerX = w/2; centerY = h/2; // 初始化数据点和控制点的位置 start.x = centerX-200; start.y = centerY; end.x = centerX+200; end.y = centerY; control.x = centerX; control.y = centerY-100; } @Override public boolean onTouchEvent(MotionEvent event) { // 根据触摸位置更新控制点，并提示重绘 control.x = event.getX(); control.y = event.getY(); invalidate(); return true; } @Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); // 绘制数据点和控制点 mPaint.setColor(Color.GRAY); mPaint.setStrokeWidth(20); canvas.drawPoint(start.x,start.y,mPaint); canvas.drawPoint(end.x,end.y,mPaint); canvas.drawPoint(control.x,control.y,mPaint); // 绘制辅助线 mPaint.setStrokeWidth(4); canvas.drawLine(start.x,start.y,control.x,control.y,mPaint); canvas.drawLine(end.x,end.y,control.x,control.y,mPaint); // 绘制贝塞尔曲线 mPaint.setColor(Color.RED); mPaint.setStrokeWidth(8); Path path = new Path(); path.moveTo(start.x,start.y); path.quadTo(control.x,control.y,end.x,end.y); canvas.drawPath(path, mPaint); } } ``` #### 三阶曲线： 三阶曲线由两个数据点和两个控制点来控制曲线状态。  代码: ``` java public class Bezier2 extends View { private Paint mPaint; private int centerX, centerY; private PointF start, end, control1, control2; private boolean mode = true; public Bezier2(Context context) { this(context, null); } public Bezier2(Context context, AttributeSet attrs) { super(context, attrs); mPaint = new Paint(); mPaint.setColor(Color.BLACK); mPaint.setStrokeWidth(8); mPaint.setStyle(Paint.Style.STROKE); mPaint.setTextSize(60); start = new PointF(0, 0); end = new PointF(0, 0); control1 = new PointF(0, 0); control2 = new PointF(0, 0); } public void setMode(boolean mode) { this.mode = mode; } @Override protected void onSizeChanged(int w, int h, int oldw, int oldh) { super.onSizeChanged(w, h, oldw, oldh); centerX = w / 2; centerY = h / 2; // 初始化数据点和控制点的位置 start.x = centerX - 200; start.y = centerY; end.x = centerX + 200; end.y = centerY; control1.x = centerX; control1.y = centerY - 100; control2.x = centerX; control2.y = centerY - 100; } @Override public boolean onTouchEvent(MotionEvent event) { // 根据触摸位置更新控制点，并提示重绘 if (mode) { control1.x = event.getX(); control1.y = event.getY(); } else { control2.x = event.getX(); control2.y = event.getY(); } invalidate(); return true; } @Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); //drawCoordinateSystem(canvas); // 绘制数据点和控制点 mPaint.setColor(Color.GRAY); mPaint.setStrokeWidth(20); canvas.drawPoint(start.x, start.y, mPaint); canvas.drawPoint(end.x, end.y, mPaint); canvas.drawPoint(control1.x, control1.y, mPaint); canvas.drawPoint(control2.x, control2.y, mPaint); // 绘制辅助线 mPaint.setStrokeWidth(4); canvas.drawLine(start.x, start.y, control1.x, control1.y, mPaint); canvas.drawLine(control1.x, control1.y,control2.x, control2.y, mPaint); canvas.drawLine(control2.x, control2.y,end.x, end.y, mPaint); // 绘制贝塞尔曲线 mPaint.setColor(Color.RED); mPaint.setStrokeWidth(8); Path path = new Path(); path.moveTo(start.x, start.y); path.cubicTo(control1.x, control1.y, control2.x,control2.y, end.x, end.y); canvas.drawPath(path, mPaint); } } ``` > 三阶曲线相比于二阶曲线可以制作更加复杂的形状，但是对于高阶的曲线，用低阶的曲线组合也可达到相同的效果，就是传说中的**降阶**。因此我们对贝塞尔曲线的封装方法一般最高只到三阶曲线。 #### 降阶与升阶 | 类型 | 释义 | 变化 | | ---- | -------------------------------- | -------------------------- | | 降阶 | 在保持曲线形状与方向不变的情况下，减少控制点数量，即降低曲线阶数 | 方法变得简单，数据点变多，控制点可能减少，灵活性变弱 | | 升阶 | 在保持曲线形状与方向不变的情况下，增加控制点数量，即升高曲线阶数 | 方法更加复杂，数据点不变，控制点增加，灵活性变强 | ### 第三步.贝塞尔曲线使用实例 **在制作这个实例之前，首先要明确一个内容，就是在什么情况下需要使用贝塞尔曲线？** > 需要绘制不规则图形时？ 当然不是！目前来说，我觉得使用贝塞尔曲线主要有以下几个方面(仅个人拙见，可能存在错误，欢迎指正) | 序号 | 内容 | 用例 | | ---- | ---------------------------- | -------------- | | 1 | 事先不知道曲线状态，需要实时计算时 | 天气预报气温变化的平滑折线图 | | 2 | 显示状态会根据用户操作改变时 | QQ小红点，仿真翻书效果 | | 3 | 一些比较复杂的运动状态(配合PathMeasure使用) | 复杂运动状态的动画效果 | 至于只需要一个静态的曲线图形的情况，用图片岂不是更好，大量的计算会很不划算。 如果是显示SVG矢量图的话，已经有相关的解析工具了(内部依旧运用的有贝塞尔曲线)，不需要手动计算。 **贝塞尔曲线的主要优点是可以实时控制曲线状态，并可以通过改变控制点的状态实时让曲线进行平滑的状态变化。** ### 接下来我们就用一个简单的示例让一个圆渐变成为心形： #### 效果图：  #### 思路分析： 我们最终的需要的效果是将一个圆转变成一个心形，通过分析可知，圆可以由四段三阶贝塞尔曲线组合而成，如下：  心形也可以由四段的三阶的贝塞尔曲线组成，如下：  两者的差别仅仅在于数据点和控制点位置不同，因此只需要调整数据点和控制点的位置，就能将圆形变为心形。 #### 核心难点： ##### 1.如何得到数据点和控制点的位置？ 关于使用绘制圆形的数据点与控制点早就已经有人详细的计算好了，可以参考stackoverflow的一个回答[How to create circle with Bézier curves?](http://stackoverflow.com/questions/1734745/how-to-create-circle-with-b%C3%A9zier-curves)其中的数据只需要拿来用即可。 而对于心形的数据点和控制点，可以由圆形的部分数据点和控制点平移后得到，具体参数可以自己慢慢调整到一个满意的效果。 ##### 2.如何达到渐变效果？ 渐变其实就是每次对数据点和控制点稍微移动一点，然后重绘界面，在短时间多次的调整数据点与控制点，使其逐渐接近目标值，通过不断的重绘界面达到一种渐变的效果。过程可以参照下图动态效果：  #### 代码： ``` java public class Bezier3 extends View { private static final float C = 0.551915024494f; // 一个常量，用来计算绘制圆形贝塞尔曲线控制点的位置 private Paint mPaint; private int mCenterX, mCenterY; private PointF mCenter = new PointF(0,0); private float mCircleRadius = 200; // 圆的半径 private float mDifference = mCircleRadius*C; // 圆形的控制点与数据点的差值 private float[] mData = new float[8]; // 顺时针记录绘制圆形的四个数据点 private float[] mCtrl = new float[16]; // 顺时针记录绘制圆形的八个控制点 private float mDuration = 1000; // 变化总时长 private float mCurrent = 0; // 当前已进行时长 private float mCount = 100; // 将时长总共划分多少份 private float mPiece = mDuration/mCount; // 每一份的时长 public Bezier3(Context context) { this(context, null); } public Bezier3(Context context, AttributeSet attrs) { super(context, attrs); mPaint = new Paint(); mPaint.setColor(Color.BLACK); mPaint.setStrokeWidth(8); mPaint.setStyle(Paint.Style.STROKE); mPaint.setTextSize(60); // 初始化数据点 mData[0] = 0; mData[1] = mCircleRadius; mData[2] = mCircleRadius; mData[3] = 0; mData[4] = 0; mData[5] = -mCircleRadius; mData[6] = -mCircleRadius; mData[7] = 0; // 初始化控制点 mCtrl[0] = mData[0]+mDifference; mCtrl[1] = mData[1]; mCtrl[2] = mData[2]; mCtrl[3] = mData[3]+mDifference; mCtrl[4] = mData[2]; mCtrl[5] = mData[3]-mDifference; mCtrl[6] = mData[4]+mDifference; mCtrl[7] = mData[5]; mCtrl[8] = mData[4]-mDifference; mCtrl[9] = mData[5]; mCtrl[10] = mData[6]; mCtrl[11] = mData[7]-mDifference; mCtrl[12] = mData[6]; mCtrl[13] = mData[7]+mDifference; mCtrl[14] = mData[0]-mDifference; mCtrl[15] = mData[1]; } @Override protected void onSizeChanged(int w, int h, int oldw, int oldh) { super.onSizeChanged(w, h, oldw, oldh); mCenterX = w / 2; mCenterY = h / 2; } @Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); drawCoordinateSystem(canvas); // 绘制坐标系 canvas.translate(mCenterX, mCenterY); // 将坐标系移动到画布中央 canvas.scale(1,-1); // 翻转Y轴 drawAuxiliaryLine(canvas); // 绘制贝塞尔曲线 mPaint.setColor(Color.RED); mPaint.setStrokeWidth(8); Path path = new Path(); path.moveTo(mData[0],mData[1]); path.cubicTo(mCtrl[0], mCtrl[1], mCtrl[2], mCtrl[3], mData[2], mData[3]); path.cubicTo(mCtrl[4], mCtrl[5], mCtrl[6], mCtrl[7], mData[4], mData[5]); path.cubicTo(mCtrl[8], mCtrl[9], mCtrl[10], mCtrl[11], mData[6], mData[7]); path.cubicTo(mCtrl[12], mCtrl[13], mCtrl[14], mCtrl[15], mData[0], mData[1]); canvas.drawPath(path, mPaint); mCurrent += mPiece; if (mCurrent < mDuration){ mData[1] -= 120/mCount; mCtrl[7] += 80/mCount; mCtrl[9] += 80/mCount; mCtrl[4] -= 20/mCount; mCtrl[10] += 20/mCount; postInvalidateDelayed((long) mPiece); } } // 绘制辅助线 private void drawAuxiliaryLine(Canvas canvas) { // 绘制数据点和控制点 mPaint.setColor(Color.GRAY); mPaint.setStrokeWidth(20); for (int i=0; i<8; i+=2){ canvas.drawPoint(mData[i],mData[i+1], mPaint); } for (int i=0; i<16; i+=2){ canvas.drawPoint(mCtrl[i], mCtrl[i+1], mPaint); } // 绘制辅助线 mPaint.setStrokeWidth(4); for (int i=2, j=2; i<8; i+=2, j+=4){ canvas.drawLine(mData[i],mData[i+1],mCtrl[j],mCtrl[j+1],mPaint); canvas.drawLine(mData[i],mData[i+1],mCtrl[j+2],mCtrl[j+3],mPaint); } canvas.drawLine(mData[0],mData[1],mCtrl[0],mCtrl[1],mPaint); canvas.drawLine(mData[0],mData[1],mCtrl[14],mCtrl[15],mPaint); } // 绘制坐标系 private void drawCoordinateSystem(Canvas canvas) { canvas.save(); // 绘制做坐标系 canvas.translate(mCenterX, mCenterY); // 将坐标系移动到画布中央 canvas.scale(1,-1); // 翻转Y轴 Paint fuzhuPaint = new Paint(); fuzhuPaint.setColor(Color.RED); fuzhuPaint.setStrokeWidth(5); fuzhuPaint.setStyle(Paint.Style.STROKE); canvas.drawLine(0, -2000, 0, 2000, fuzhuPaint); canvas.drawLine(-2000, 0, 2000, 0, fuzhuPaint); canvas.restore(); } } ``` ## 三.总结 其实关于贝塞尔曲线最重要的是核心理解贝塞尔曲线的生成方式，只有理解了贝塞尔曲线的生成方式，才能更好的运用贝塞尔曲线。在上一篇末尾说本篇要涉及一点自相交图形渲染问题，不幸的是，本篇没有了，请期待下一篇(可能会在下一篇中出现o(*￣︶￣*)o)，下一篇依旧Path相关内容，教给大家一些更好玩的东西。 解锁新的境界之[【绘制一个弹性的圆】](http://www.jianshu.com/p/791d3a791ec2)： <img src="http://ww3.sinaimg.cn/large/005Xtdi2jw1f3cij475bhg30k00zk46m.gif" width=300 /> (,,• ₃ •,,) #### PS: 由于本人水平有限，某些地方可能存在误解或不准确，如果你对此有疑问可以提交Issues进行反馈。 ## About Me ### 作者微博: <a href="http://weibo.com/GcsSloop" target="_blank">@GcsSloop</a> <a href="https://github.com/GcsSloop/AndroidNote/blob/magic-world/FINDME.md" target="_blank"> <img src="http://ww4.sinaimg.cn/large/005Xtdi2gw1f1qn89ihu3j315o0dwwjc.jpg" width=300/> </a> ## 参考资料 [Path](http://developer.android.com/reference/android/graphics/Path.html)<br/> [Canvas](http://developer.android.com/reference/android/graphics/Canvas.html)<br/> [贝塞尔曲线扫盲](http://www.html-js.com/article/1628)<br/> [贝塞尔曲线-维基百科](https://zh.wikipedia.org/wiki/%E8%B2%9D%E8%8C%B2%E6%9B%B2%E7%B7%9A)<br/> [How to create circle with Bézier curves?](http://stackoverflow.com/questions/1734745/how-to-create-circle-with-b%C3%A9zier-curves)<br/> [三次贝塞尔曲线练习之弹性的圆](http://www.jianshu.com/p/791d3a791ec2)<br/>