## **堆排序**
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆排序就是把最大堆堆顶的最大数取出,将剩余的堆继续调整为最大堆,再次将堆顶的最大数取出,这个过程持续到剩余数只有一个时结束。
## **堆的概念**
堆是一种特殊的完全二叉树(complete binary tree)。完全二叉树的一个“优秀”的性质是,除了最底层之外,每一层都是满的,这使得堆可以利用数组来表示(普通的一般的二叉树通常用链表作为基本容器表示),每一个结点对应数组中的一个元素。
如下图,是一个堆和数组的相互关系:
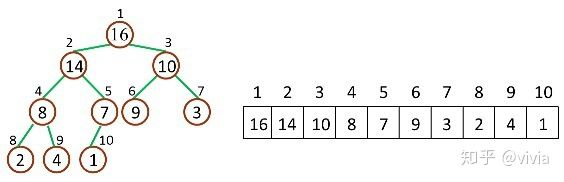
对于给定的某个结点的下标 i,可以很容易的计算出这个结点的父结点、孩子结点的下标:
* Parent(i) = floor(i/2),i 的父节点下标
* Left(i) = 2i,i 的左子节点下标
* Right(i) = 2i + 1,i 的右子节点下标
二叉堆一般分为两种:最大堆和最小堆。
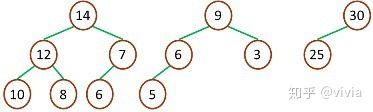
**最大堆:**
最大堆中的最大元素值出现在根结点(堆顶)
堆中每个父节点的元素值都大于等于其孩子结点(如果存在)
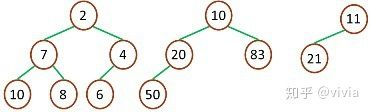
**最小堆:**
最小堆中的最小元素值出现在根结点(堆顶)
堆中每个父节点的元素值都小于等于其孩子结点(如果存在)
## **堆排序原理**
堆排序就是把最大堆堆顶的最大数取出,将剩余的堆继续调整为最大堆,再次将堆顶的最大数取出,这个过程持续到剩余数只有一个时结束。在堆中定义以下几种操作:
* 最大堆调整(Max-Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
* 创建最大堆(Build-Max-Heap):将堆所有数据重新排序,使其成为最大堆
* 堆排序(Heap-Sort):移除位在第一个数据的根节点,并做最大堆调整的递归运算 继续进行下面的讨论前,需要注意的一个问题是:数组都是 Zero-Based,这就意味着我们的堆数据结构模型要发生改变
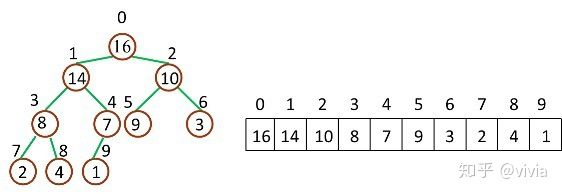
相应的,几个计算公式也要作出相应调整:
* Parent(i) = floor((i-1)/2),i 的父节点下标
* Left(i) = 2i + 1,i 的左子节点下标
* Right(i) = 2(i + 1),i 的右子节点下标
## **堆的建立和维护**
堆可以支持多种操作,但现在我们关心的只有两个问题:
1. 给定一个无序数组,如何建立为堆?
2. 删除堆顶元素后,如何调整数组成为新堆?
先看第二个问题。假定我们已经有一个现成的大根堆。现在我们删除了根元素,但并没有移动别的元素。想想发生了什么:根元素空了,但其它元素还保持着堆的性质。我们可以把**最后一个元素**(代号A)移动到根元素的位置。如果不是特殊情况,则堆的性质被破坏。但这仅仅是由于A小于其某个子元素。于是,我们可以把A和这个子元素调换位置。如果A大于其所有子元素,则堆调整好了;否则,重复上述过程,A元素在树形结构中不断“下沉”,直到合适的位置,数组重新恢复堆的性质。上述过程一般称为“筛选”,方向显然是自上而下。
> 删除后的调整,是把最后一个元素放到堆顶,自上而下比较
删除一个元素是如此,插入一个新元素也是如此。不同的是,我们把新元素放在**末尾**,然后和其父节点做比较,即自下而上筛选。
> 插入是把新元素放在末尾,自下而上比较
那么,第一个问题怎么解决呢?
常规方法是从第一个非叶子结点向下筛选,直到根元素筛选完毕。这个方法叫“筛选法”,需要循环筛选n/2个元素。
但我们还可以借鉴“插入排序”的思路。我们可以视第一个元素为一个堆,然后不断向其中添加新元素。这个方法叫做“插入法”,需要循环插入(n-1)个元素。
由于筛选法和插入法的方式不同,所以,相同的数据,它们建立的堆一般不同。大致了解堆之后,堆排序就是水到渠成的事情了。
## **算法描述**
我们需要一个升序的序列,怎么办呢?我们可以建立一个最小堆,然后每次输出根元素。但是,这个方法需要额外的空间(否则将造成大量的元素移动,其复杂度会飙升到O(n2) )。如果我们需要就地排序(即不允许有O(n)空间复杂度),怎么办?
有办法。我们可以建立最大堆,然后我们倒着输出,在最后一个位置输出最大值,次末位置输出次大值……由于每次输出的最大元素会腾出第一个空间,因此,我们恰好可以放置这样的元素而不需要额外空间。很漂亮的想法,是不是?
## **稳定性**
堆排序存在大量的筛选和移动过程,属于不稳定的排序算法。
## **适用场景**
堆排序在建立堆和调整堆的过程中会产生比较大的开销,在元素少的时候并不适用。但是,在元素比较多的情况下,还是不错的一个选择。尤其是在解决诸如“前n大的数”一类问题时,几乎是首选算法。
## **JAVA代码实现**
```
public class ArrayHeap {
private int[] arr;
public ArrayHeap(int[] arr) {
this.arr = arr;
}
private int getParentIndex(int child) {
return (child - 1) / 2;
}
private int getLeftChildIndex(int parent) {
return 2 * parent + 1;
}
private void swap(int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/**
* 调整堆。
*/
private void adjustHeap(int i, int len) {
int left, right, j;
left = getLeftChildIndex(i);
while (left <= len) {
right = left + 1;
j = left;
if (j < len && arr[left] < arr[right]) {
j++;
}
if (arr[i] < arr[j]) {
swap(array, i, j);
i = j;
left = getLeftChildIndex(i);
} else {
break; // 停止筛选
}
}
}
/**
* 堆排序。
* */
public void sort() {
int last = arr.length - 1;
// 初始化最大堆
for (int i = getParentIndex(last); i >= 0; --i) {
adjustHeap(i, last);
}
// 堆调整
while (last >= 0) {
swap(0, last--);
adjustHeap(0, last);
}
}
}
```
- JDK常用知识库
- JDK各个版本安装
- Java8流
- 算法
- 十大排序算法
- 冒泡排序
- 选择排序
- 插入排序
- 归并排序
- 快速排序
- 堆排序
- 希尔排序
- 计数排序
- 桶排序
- 基数排序
- 总结
- 常用工具类
- 浮点型计算
- 时间格式处理
- 常用功能点思路整理
- 登录
- 高并发
- 线程安全的单例模式
- Tomcat优化
- Tomcat之APR模式
- Tomcat启动过慢问题
- 常用的数据库连接池
- Druid连接池
- 缓存
- Redis
- SpringBoot整合Redis
- 依赖和配置
- RedisTemplate工具类
- 工具类使用方法
- Redis知识库
- Redis安装
- Redis配置参数
- Redis常用Lua脚本
- MongoDB
- SpringBoot操作MongoDB
- 依赖和配置
- MongoDB工具类
- 工具类使用方法
- 消息中间件
- ActiveMq
- SpringBoot整合ActiveMq
- 框架
- SpringBoot
- 定时任务
- 启动加载
- 事务
- JSP
- 静态类注入
- SpringSecurity
- Shiro
- 配置及整合
- 登陆验证
- 权限验证
- 分布式应用
- SpringMVC
- ORM框架
- Mybatis
- 增
- 删
- 改
- 查
- 程序员小笑话
- 我给你讲一个TCP的笑话吧
- 二进制笑话
- JavaScript的那点东西
- JavaScript内置对象及常见API详细介绍
- JavaScript实现Ajax 资源请求
- JavaScript干货
- 架构师成长之路
- JDK源码解析
- ArrayList源码解读
- 设计模式
- 微服务架构设计模式
- 逃离单体炼狱
- 服务的拆分策略
- 全面解析SpringMvc框架
- 架构设计的六大原则
- 并发集合
- JUC并发编程
- 搜索引擎
- Solr
- Solr的安装
- 分布式服务框架
- Dubbo
- 从零开始学HTMl
- 第一章-初识HTML
- 第二章-认识HTML标签
