[toc]
# 时间复杂度
一段代码运行的时间。
## 分析代码执行的次数
通过分析 `代码执行的条数` 来衡量时间复杂度。
比如:
~~~
function hello() {
console.log('hello')
}
~~~
这个函数执行了 1 代码。 渐进复杂度:O(1)
再比如:
~~~
function hello1() {
console.log('hello');
console.log('hello');
console.log('hello')
}
~~~
这个函数执行的代码次数是 3。 O(1)
再比如:
~~~
function hello2() {
for(let i=0;i<20;i++) {
console.log('hello')
}
}
~~~
这段代码我们就说,这段代码执行了20次语句。
~~~
function hello3() {
for(let i=0;i<20;i++) {
console.log('hello')
console.log('hello')
console.log('hello')
}
}
~~~
这段代码花费的时间是:60 O(1)
~~~
function hello4(n) {
for(let i=0;i<n;i++) {
console.log('hello')
console.log('hello')
console.log('hello')
}
}
~~~
这段代码花费的时间是:3n O(n)
~~~
function hello5(n) {
for(let i=0;i<n;i++) {
console.log('hello') // 被执行 n 次
console.log('hello') // 被执行 n 次
for(let j=0;j<n;j++) {
console.log('hello') // 被执行 n * n 次(n的平方)
console.log('hello') // 被执行 n * n 次(n的平方)
}
}
}
~~~
这段代码花费的时间是:n + n + n^2 + n^2 = 2n + 2n^2 = 2(n^2+n) O(n^2)
总结:代码花费的时间主要就是通过代码被执行的次数来判断,有一些复杂的代码是需要很强的数学功底才能算出执行的次数,对于此我们知道常见的即可。
练习:以下代码执行次数是多少?
~~~
function hello6(n) {
for(let i=0;i<n;i++) {
if(n%2==0) {
console.log('hello') // n/2
}
console.log('hello') // n
for(let j=0;j<n;j++) {
console.log('hello') // n^2
}
}
}
~~~
代码执行的次数:n^2 + 1.5n O(n^2)
~~~
function hello7(n) {
for(let i=n;i>=0;i=i/2) {
console.log('hello') // log2N(开对数,log 以2为底的n)
}
}
~~~
代码执行的次数:logn(默认以2为底) O(logn)
## 渐进时间复杂度
实际工作中,代码执行次数计算的再精确意义也不大,比如:两代码。
代码 a 的执行次数:100n。
代码 b 的执行次数:n^2。
这时两段如何判断谁的性能更好?
当 n 小时,代码b快,当n值大时,代码a快。
所以,我们一般采用 `渐进的时间复杂度` 来衡量:当 n 无限增大时,代码执行次数增长的趋势。
所以我们平时说的时间复杂度,其实是指:`渐进时间复杂度`。
在计算渐进时间复杂度时有以下几个原则:
1. 变量前面的系统数,一般直接忽略,比如:10n --> n
2. 如果有最高阶,只保留最阶,比如:n^5 + n^2 ---> n^5
3. 如果代码执行的次数稳定不变,那么就用 1 来表示,比如: 5 --> 1
使用 大O 表示法的符号来表示渐进复杂度。
比如:以下代码执行次数是 2(n^2+n),那么它的渐进时间复杂度用大O表示法来表示:
~~~
function hello5(n) {
for(let i=0;i<n;i++) {
console.log('hello') // 被执行 n 次
console.log('hello') // 被执行 n 次
for(let j=0;j<n;j++) {
console.log('hello') // 被执行 n * n 次(n的平方)
console.log('hello') // 被执行 n * n 次(n的平方)
}
}
}
~~~
渐进时间复杂度为:O(n^2)
总结:
1. 使用大O表示法来表示一段代码的时间复杂度
2. 大O代表的是`渐进时间复杂度`:当n无限增大,代码花费时间的增长趋势。
分析一段代码的时间复杂度的流程:
1. 先分析代码执行的次数,得到一个公式
2. 根据规则转成 大O 表示法
## 常见的几种时间复杂度
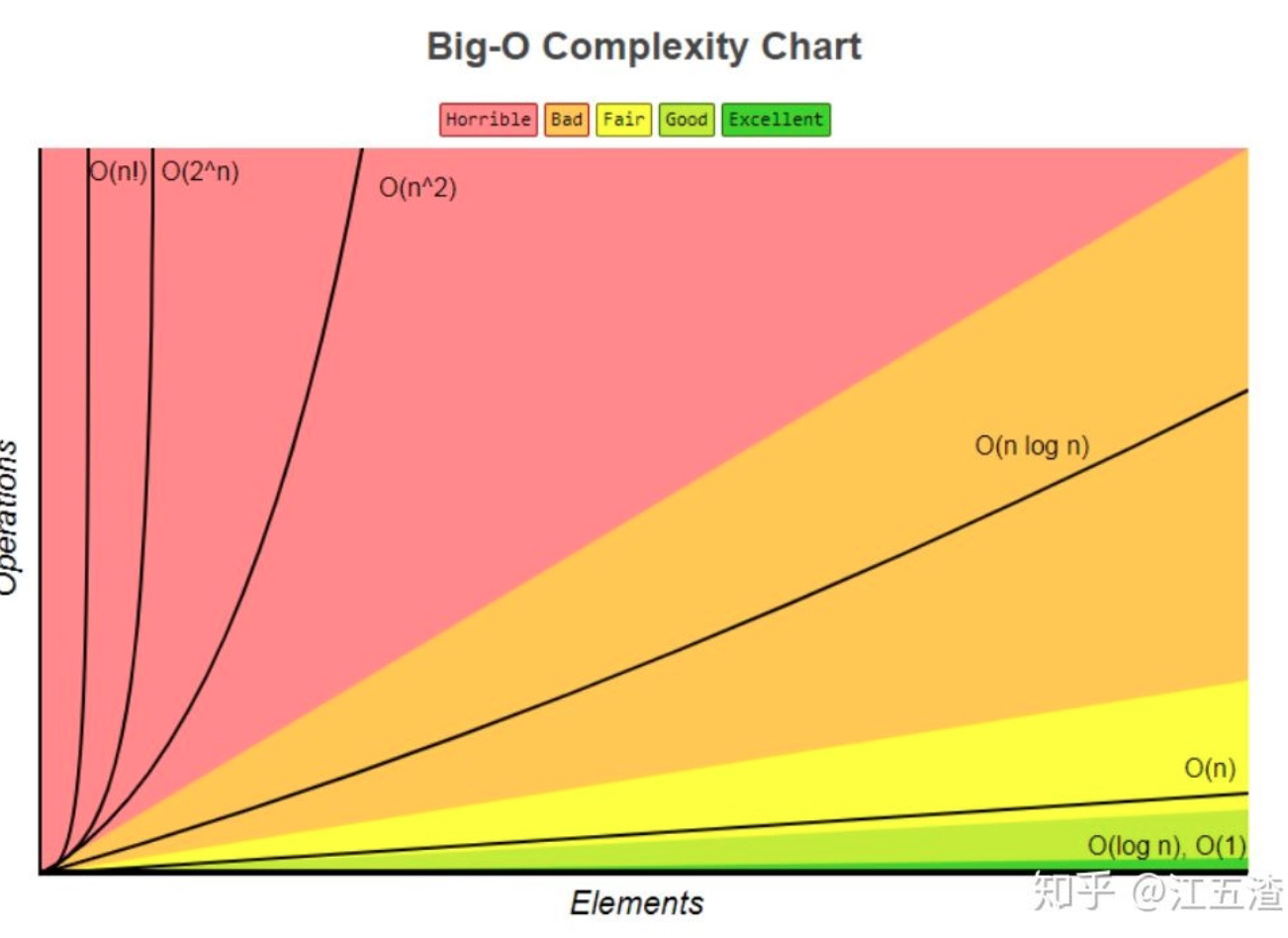
# 最好、平均、最坏时间复杂度
一段代码的时间复杂度还和要操作的数据相关,比如:如果要排序一个数组,然后这个数组是已经排序好的数组,那么对这个数组进行排序,速度会非常快。这属于最好情况。
所以我们一般说时间复杂度时,一般都是是指:“最坏时间复杂度”。
