> 引用:[https://www.cnblogs.com/chengxiao/p/6129630.html](https://www.cnblogs.com/chengxiao/p/6129630.html)
堆的概念:
1. 堆就是一个棵二叉树(每个节点 `最多有两个子节点` 的结构)
2. 大顶堆:每个节点的值都比子节点的值大(所以,堆顶元素肯定是最大的)
3. 大顶堆:每个节点的值都比子节点的值小(所以,堆顶元素肯定是最小的)
堆可以保存在数组中,在数组中的特点:
第 i 个节点的 左子节点下标是 2i+1
右子节点下标是 2i+2
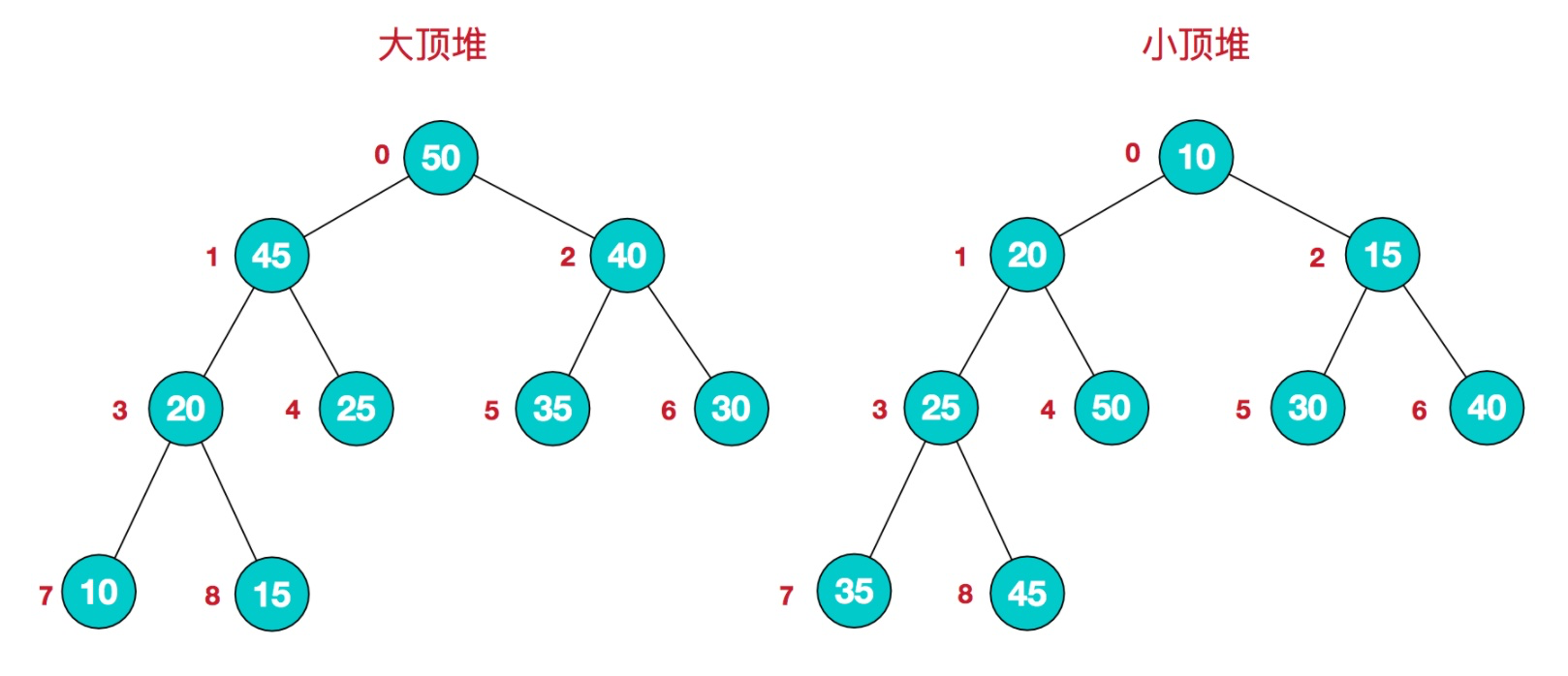
在数组中使用编号来表示:

堆排序的实现思路:
1. 先把数组构造成一个大顶堆
2. 把顶堆元素(最大)放到数组的最后
3. 把数组中除了最后一个元素(已经排好序的最大元素)之外的数组当成一个数组,重新构造成一个大顶堆
4. 再把堆顶(下标为0)元素(第2大)放到数组倒数第2 的位置以此类推 ....
# 实现
## 步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
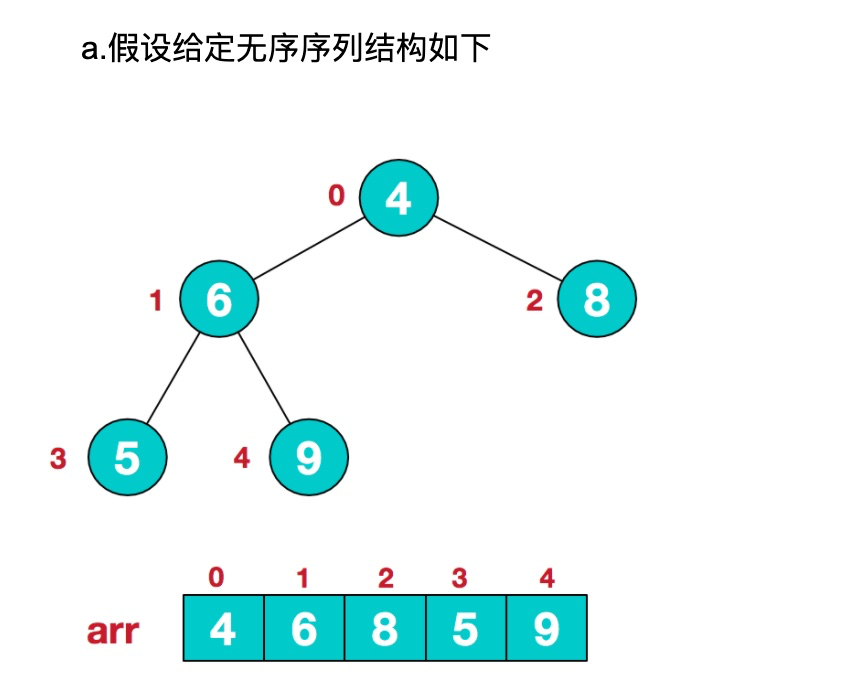
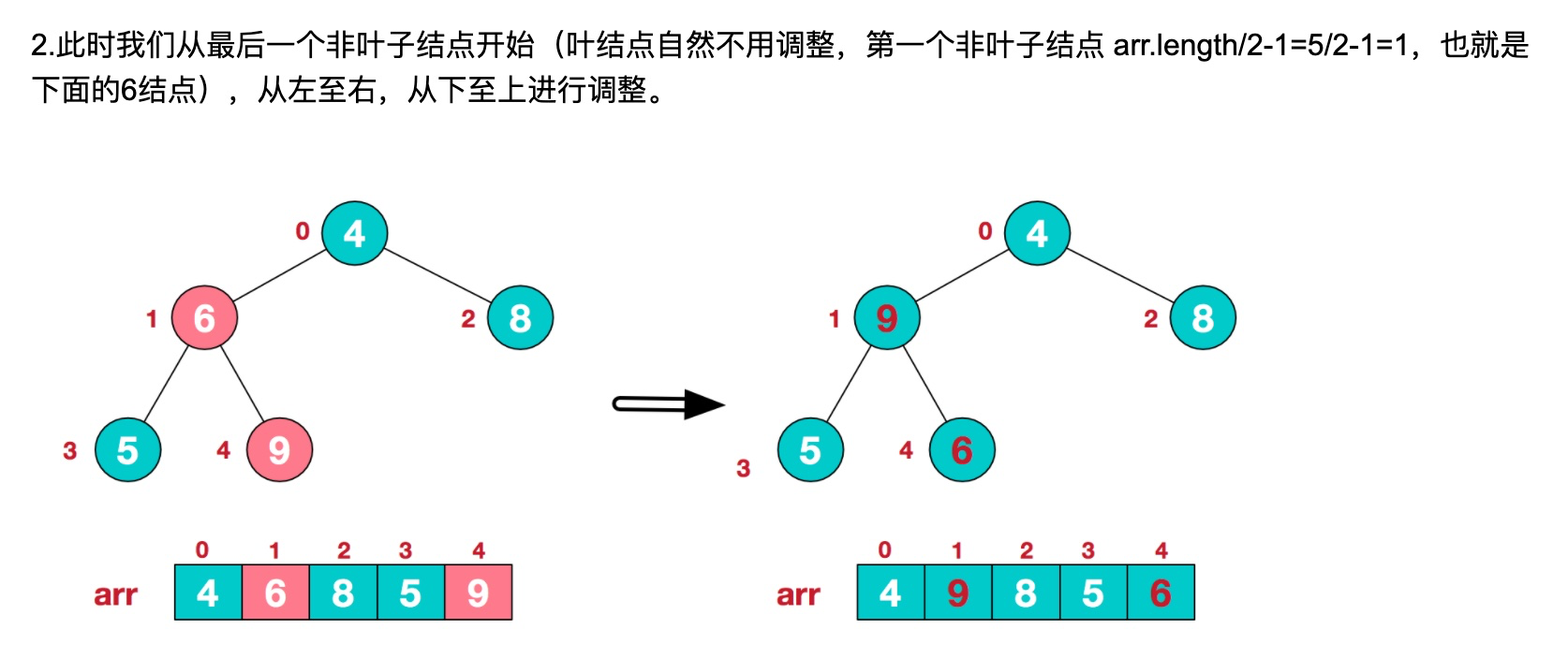
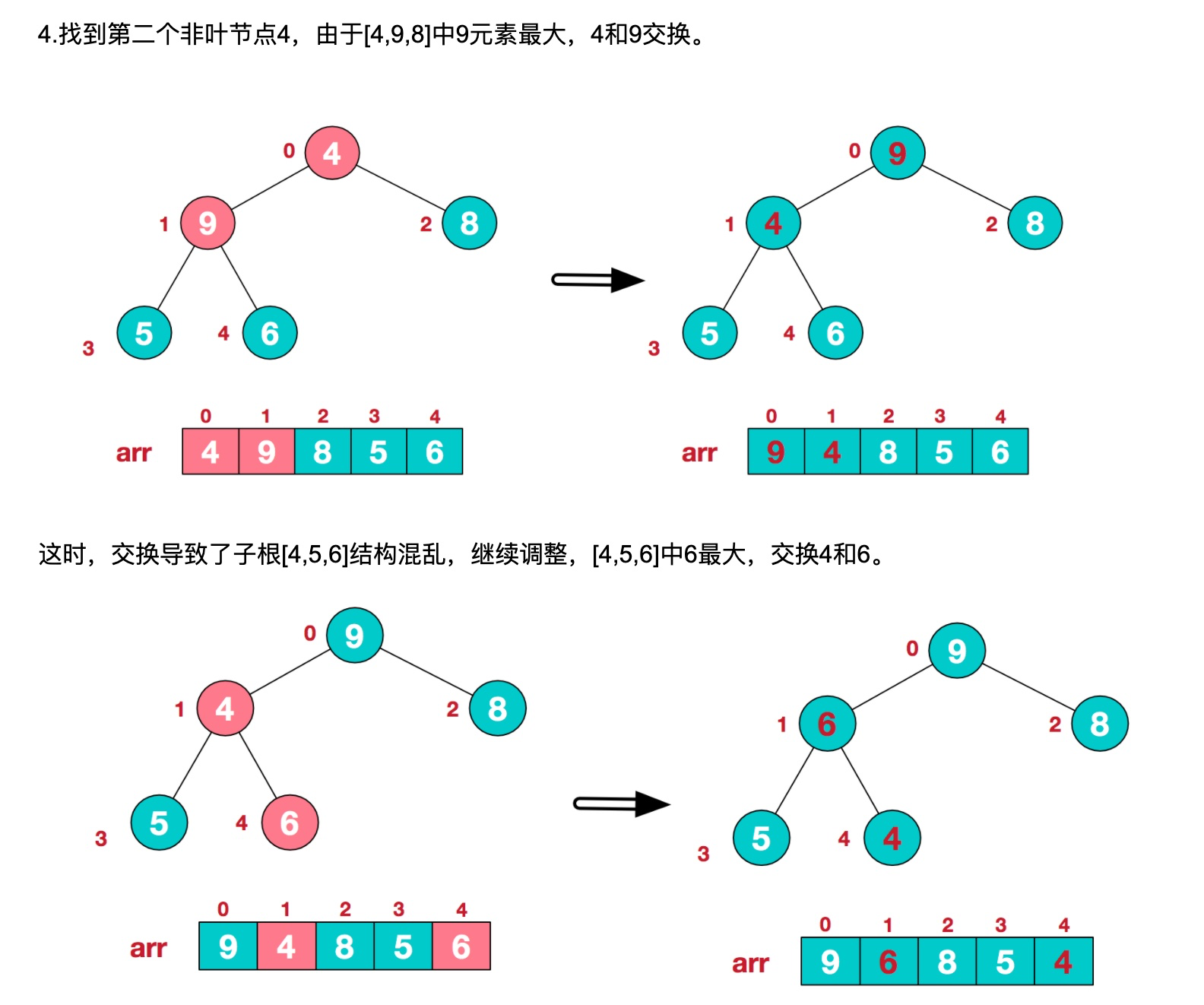
此时,我们就将一个无需序列构造成了一个大顶堆。
## 步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整et堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。

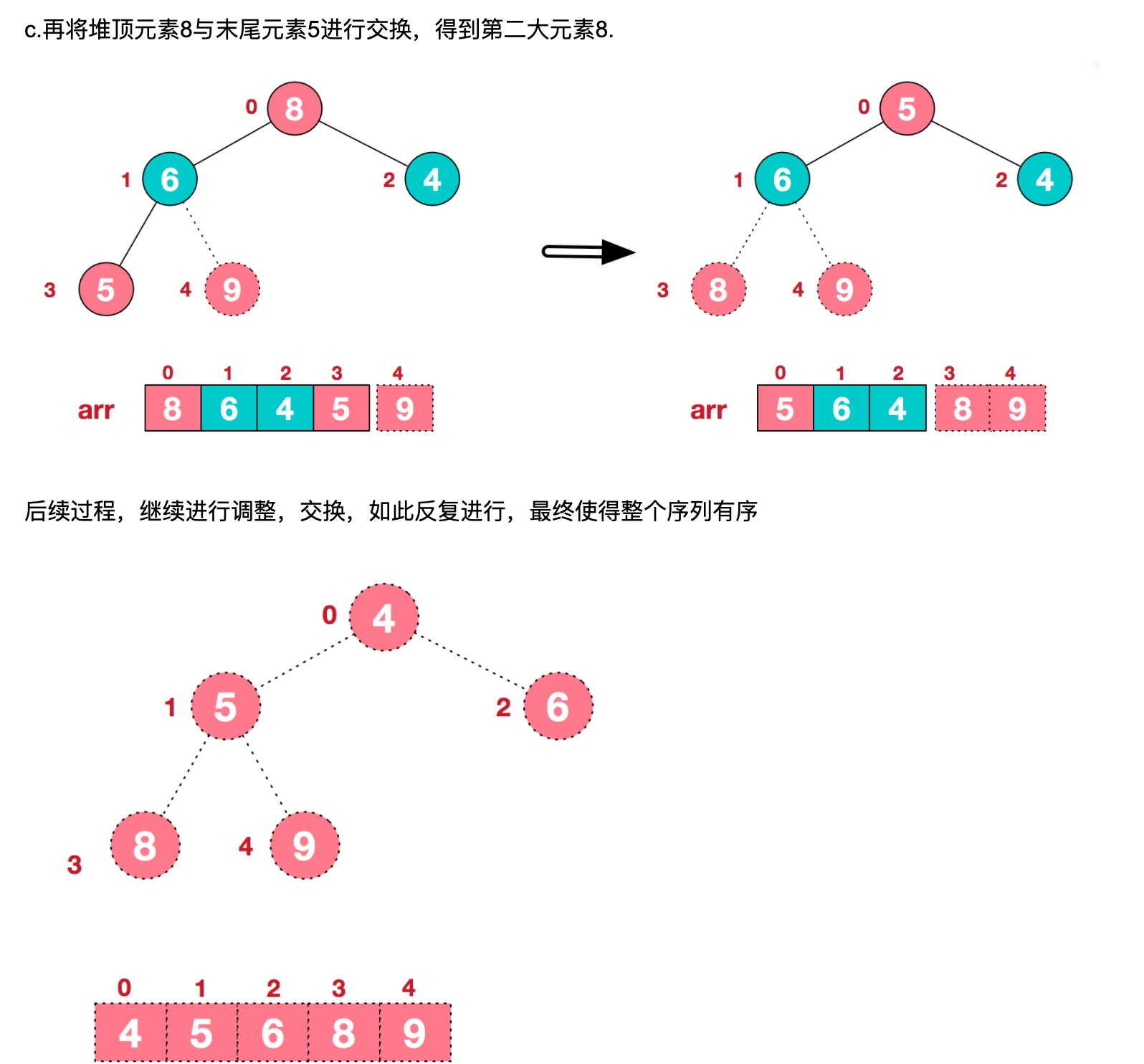
# JavaScript
~~~
let len
function heapSort(arr) {
len = arr.length
// 1. 从最后一个“非叶子节点”(len/2-1)构造大顶堆
for(let i=Math.floor(len/2)-1;i>=0;i--) {
// 调整节点为大顶
heapify(arr, i)
}
// 2. 依次把根节点移动到数组最后,并重新调整大顶堆
for(let i=arr.length-1;i>0;i--) {
// 把第一个元素(最大的)交换到最后
[arr[0],arr[i]] = [arr[i],arr[0]]
// 长度减少(以后省略最后一个元素)
len--
// 从根节点开始重新调整为大顶堆
heapify(arr, 0)
}
}
function heapify(arr, i) {
let left = 2*i+1,
right = 2*i + 2,
largest = i // 默认节点为最大元素
// 如果有左子节点,并且左子节点大于父节点
if(left < len && arr[left] > arr[largest]) {
// 标记左子节点更大
largest=left
}
// 如果有右子节点,并且右子节点大于父节点
if(right < len && arr[right] > arr[largest]) {
// 标记右子节点更大
largest=right
}
// 如果标记最大的元素不是父节点
if(i!=largest) {
// 那么父节点和大的子节点交换
[arr[i],arr[largest]] = [arr[largest],arr[i]]
// 对交换之后的节点再次调整
heapify(arr, largest)
}
}
~~~
