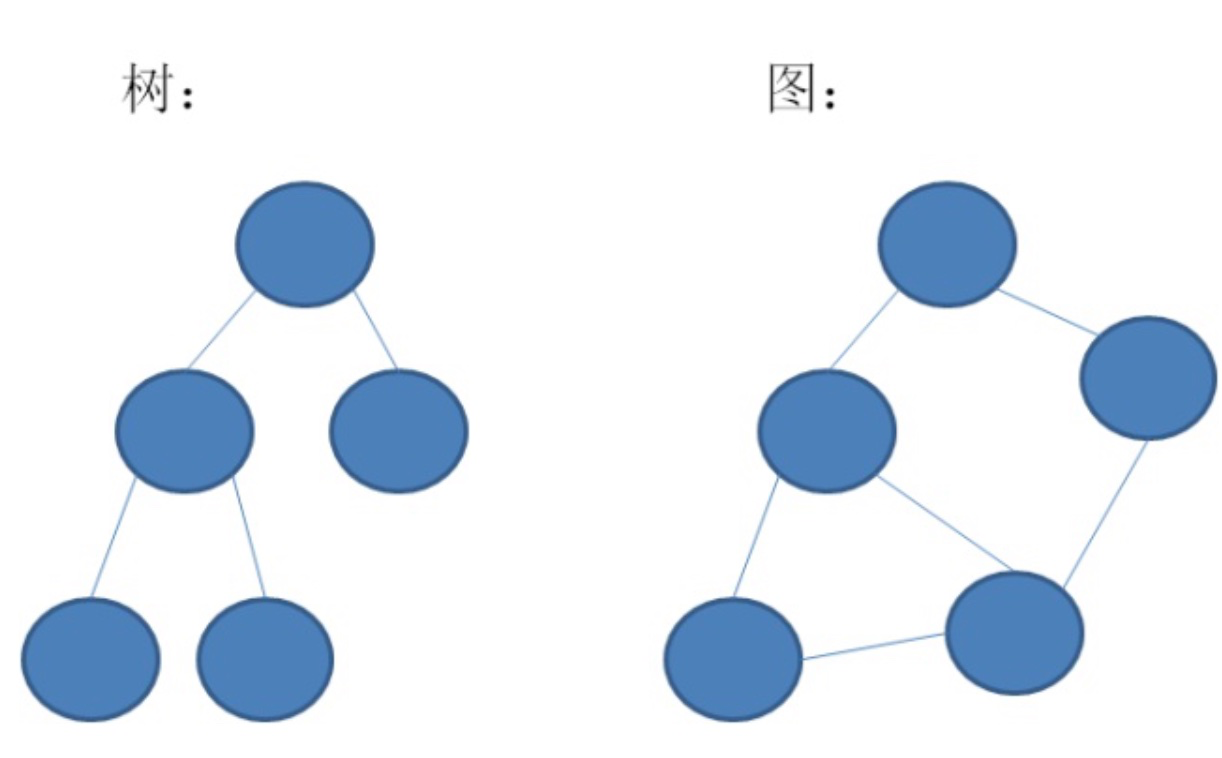
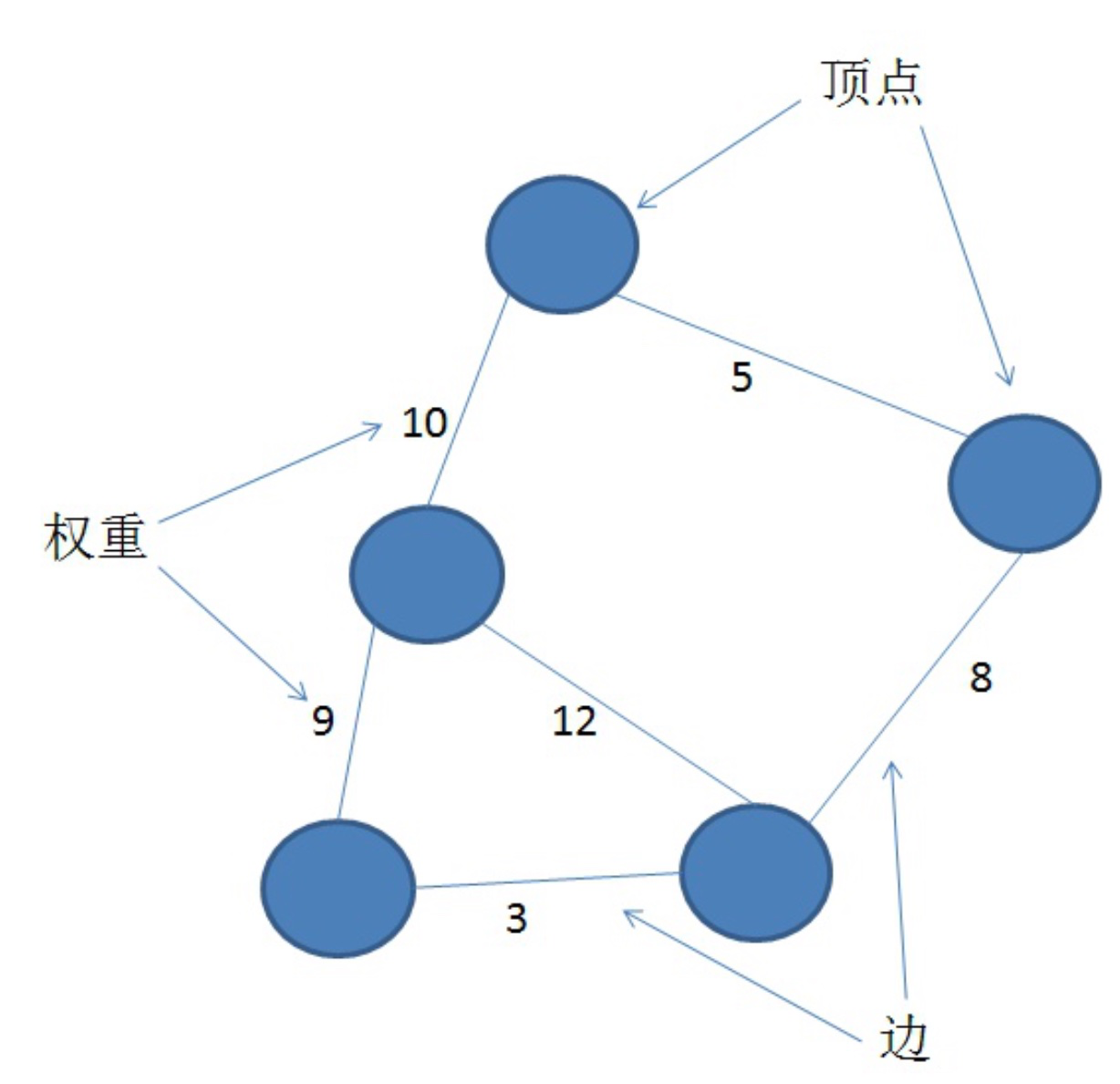
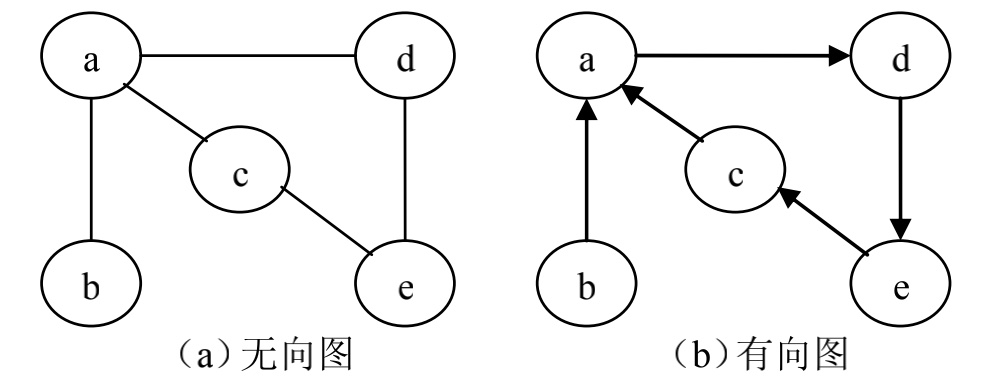
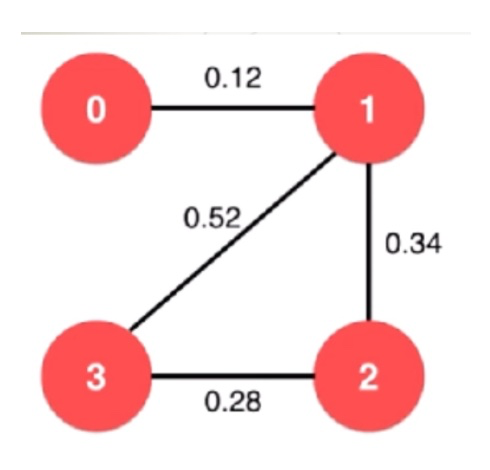
> 引用：[https://www.cnblogs.com/jaxu/p/11338294.html](https://www.cnblogs.com/jaxu/p/11338294.html) # 介绍 多对多的一种数据结构。 图：一些顶点和一些边的集合。  ## 术语  # 分类 ## 有向图和无向图  ## 入度和出度 对于 `有向图` 来说。 入度：进入一个顶点的边数。 出席：从一个顶点出去的边数。 ## 有权图  # 连通性 ### 连通图 1. 从一个顶点到另一顶点，若存在至少一条路径，则称两个顶点是连通的。 2. 在 `无向图` 中，若任意两个顶点都连通，则图是连通图。  ### 强连通图 在 `有向图` 中，若任意两个顶点都含有至少一条通路，则图是强连通图。  ## 连通网 在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。  # 生成树 对 `连通图` 进行遍历时，遍历过程中所经过的 `边` 和 `顶点` 的组合可看做是一棵普通树，通常称为生成树。 如下图，a为连通图，b为生成树。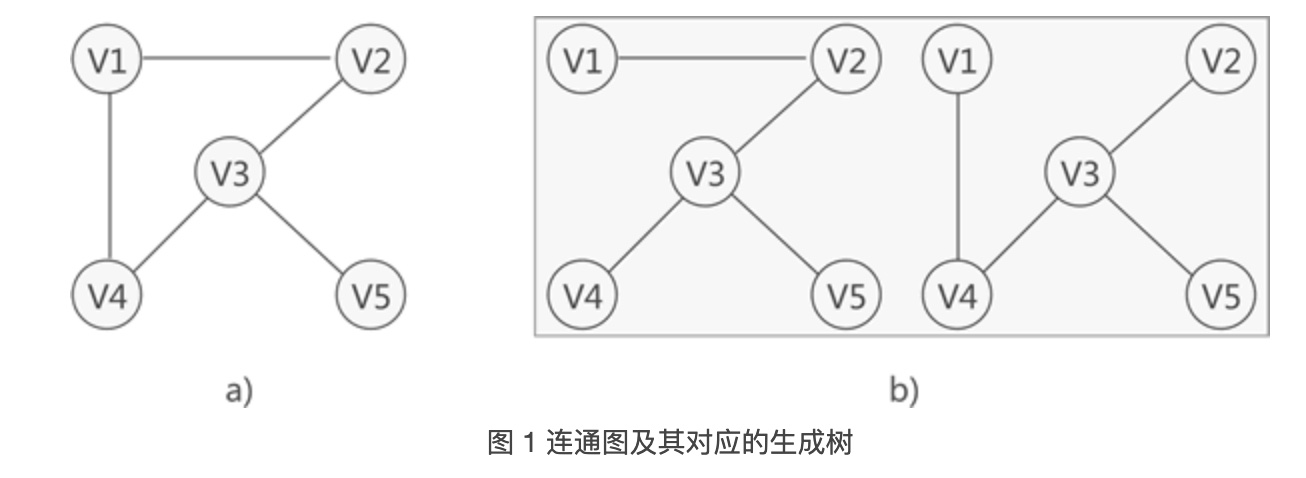  因为连通图中有多个边，所以一个连通图可能会有多个生成树。