# 介绍
1. AVL 树是最早被发明的自平衡二叉树
2. AVL 树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis,他们在1962年的论文中发表了它。
# 构建 AVL 树
为了保证一树是时刻保持平衡,我们需要在向节点中插入、删除新节点时通过 `旋转` 来调整树的结构。
如何实现二叉树调整平衡,要通过二叉树的 `旋转` 来实现。
二叉树可以分为四种情况,不同的情况进行不同的旋转:
L:left 左
LL: 左左型
R:right 右
RR:右右型
LR:左右型
RL:右左型
* LL型二叉树 :右旋转
* RR型二叉树:左旋转
* LR型二叉树:先左旋转再右旋转
* RL型二叉树:先右旋转再左旋转
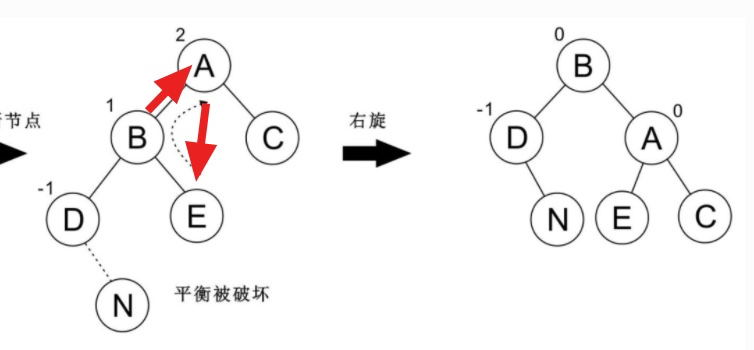
## LL 型
对于节点倾向于左边的情况,我们称之为 `LL型`。
这个时候我们需要进行 `右旋转` 操作,使它恢复平衡:
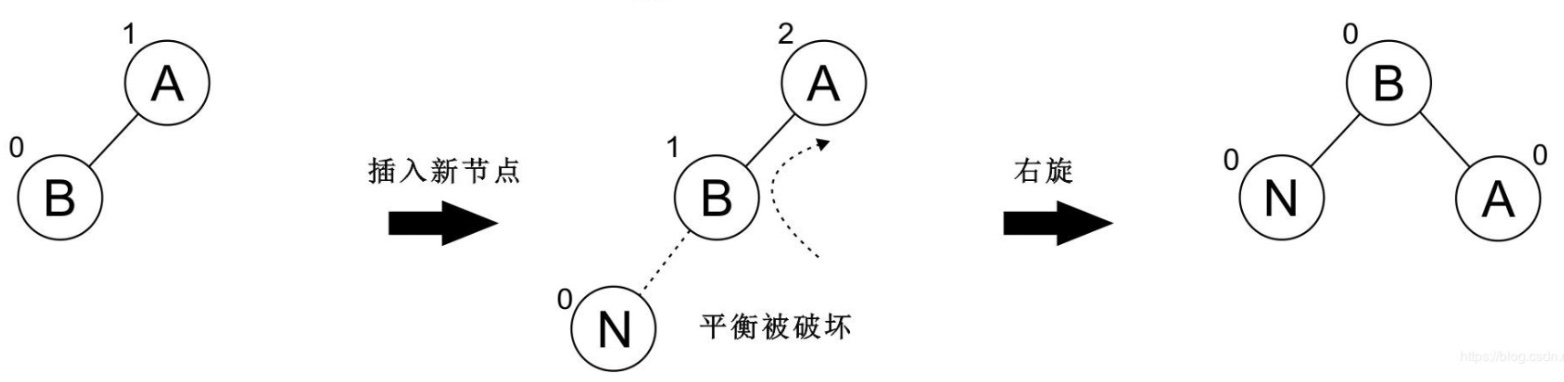
再看一个例子:
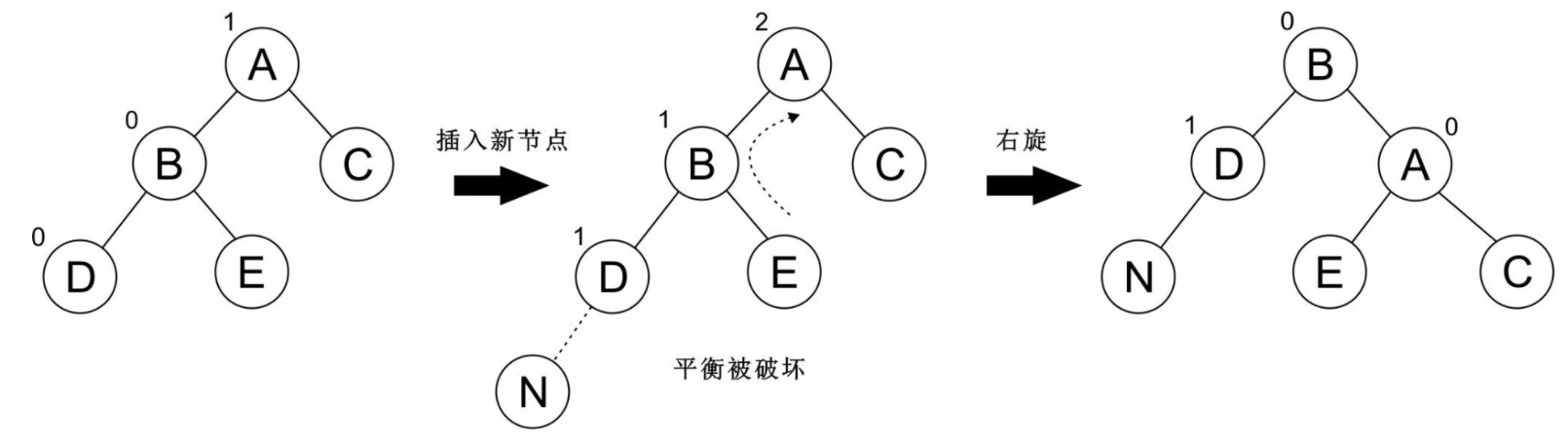
再看一个例子:

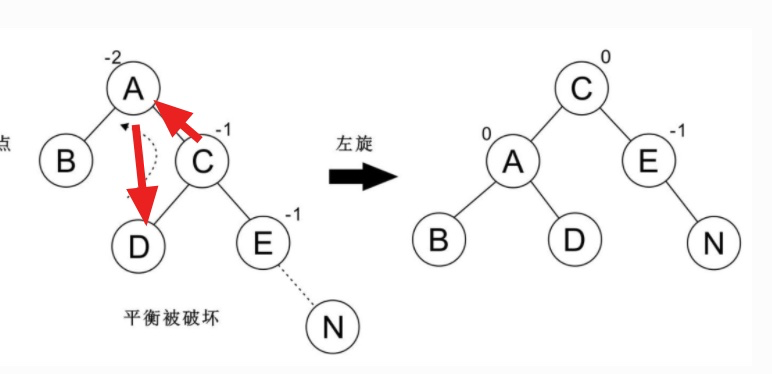
## RR 型
对于节点倾向于右边的情况,我们称之为 `RR型`。
这个时候我们需要进行 `左旋转` 操作,使它恢复平衡:
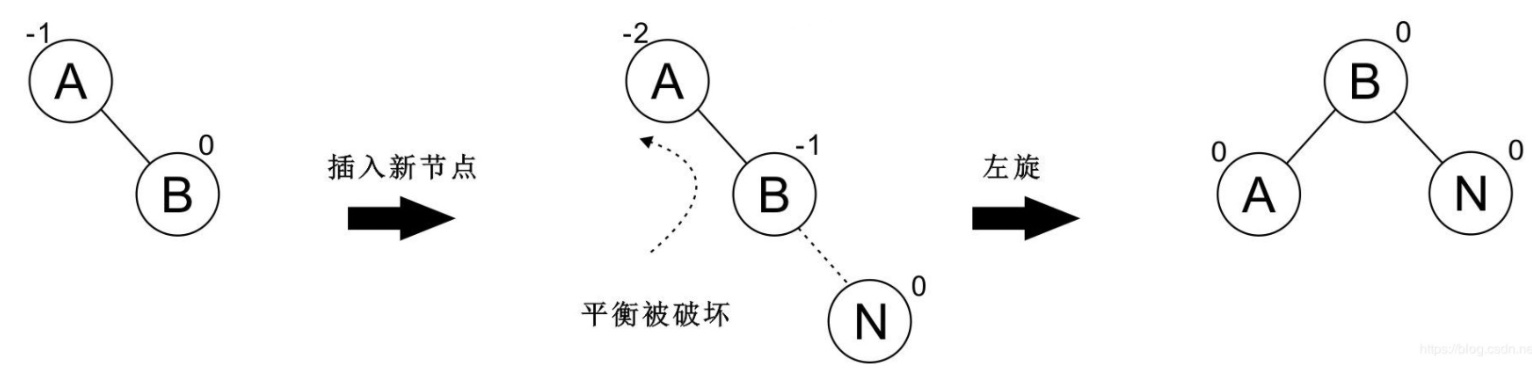
再看一个例子:
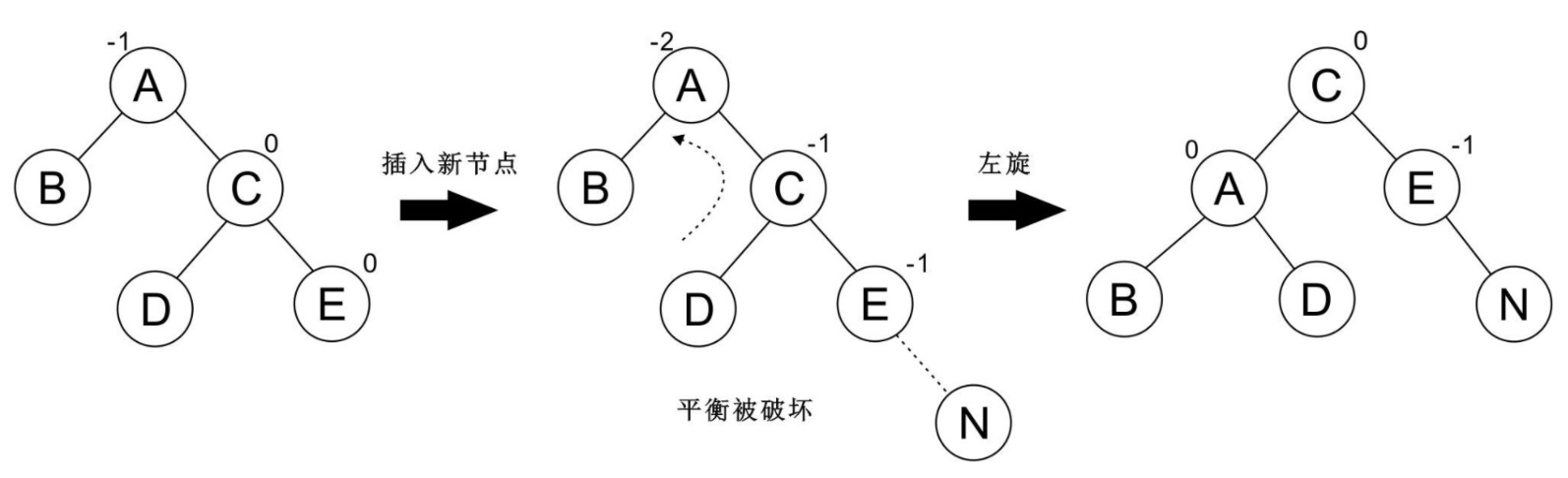
再看一个例子:

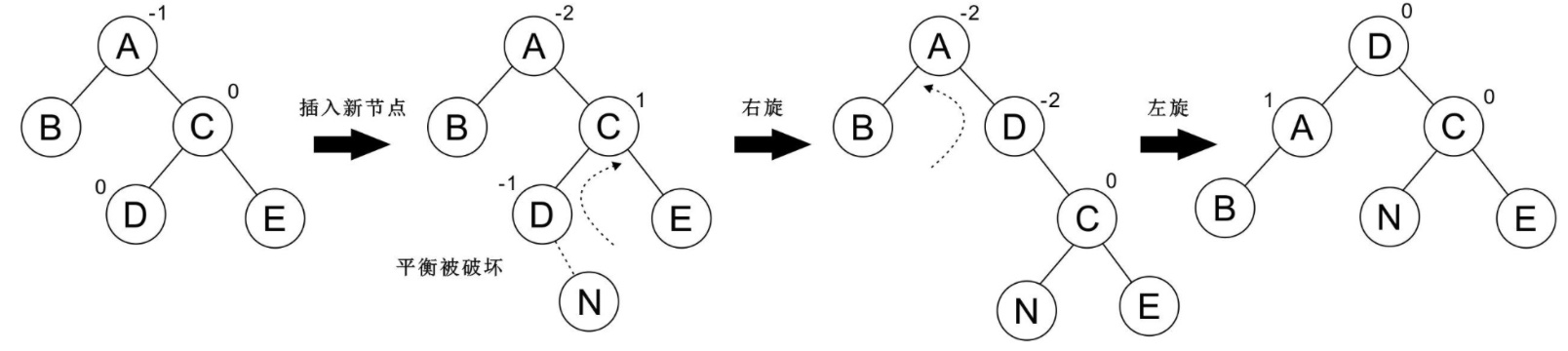
## LR 型
以下树为 LR 型,这种情况需要旋转两次:先左旋转再右旋转:
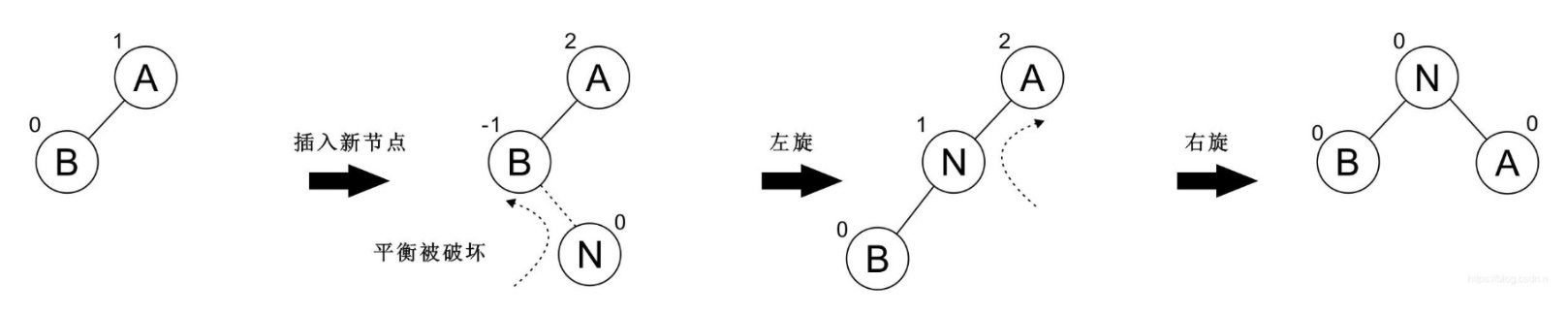
再看一个例子:
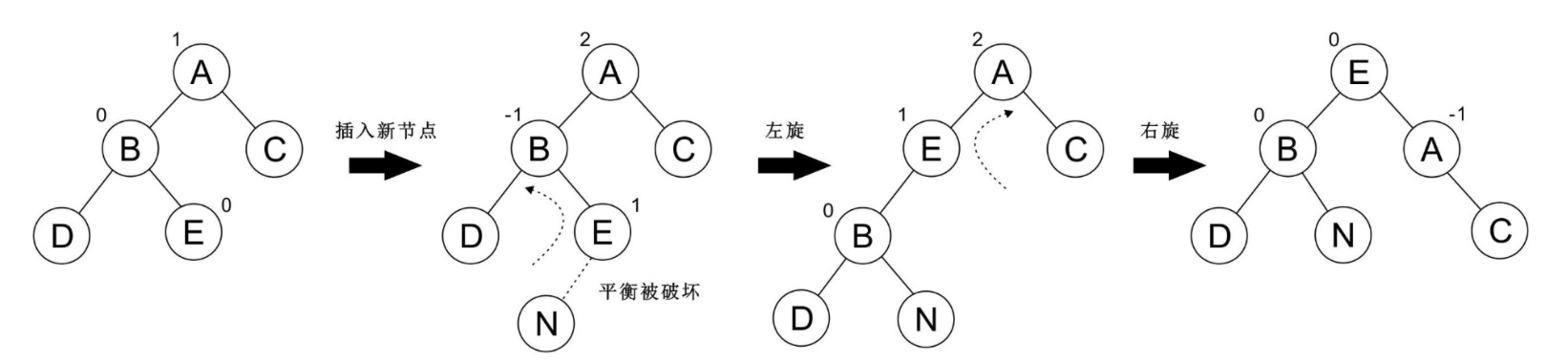
再看一个例子:
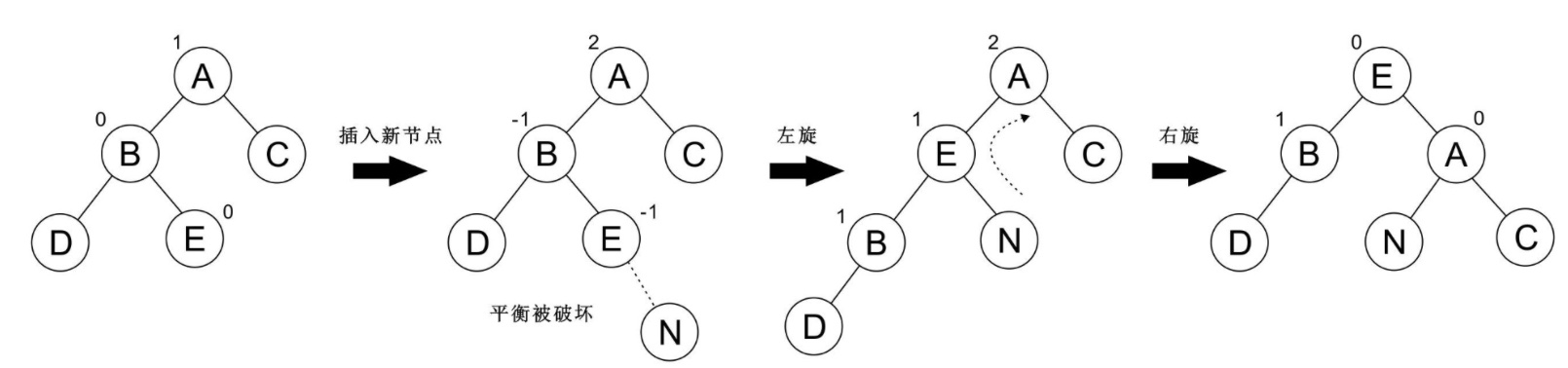
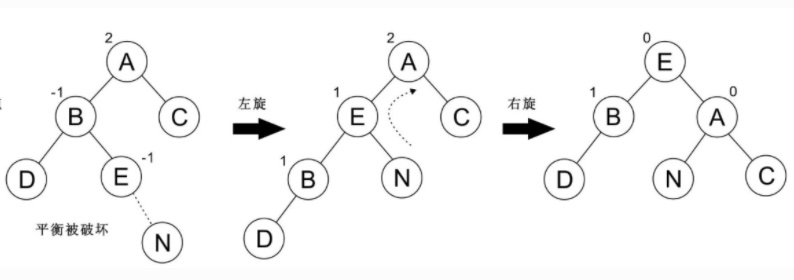
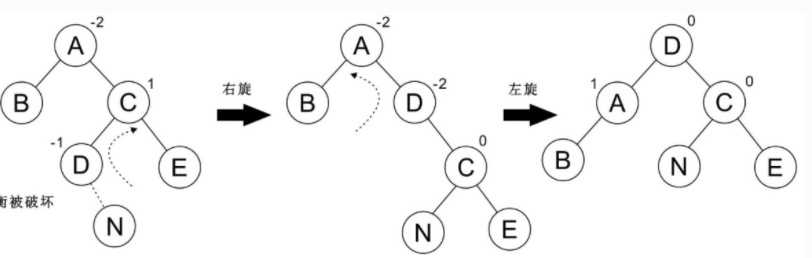
## RL 型
看一个例子:

再看一个例子:
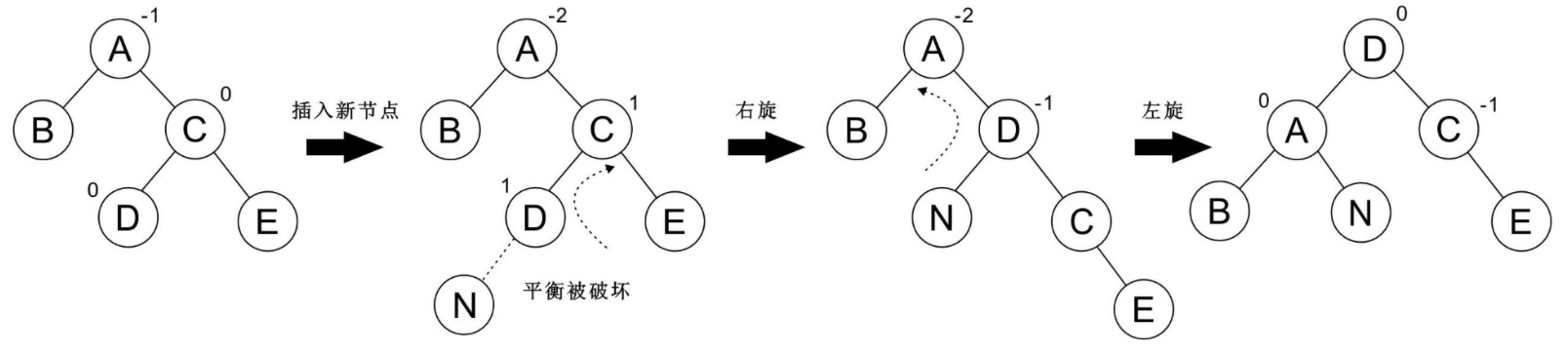
再看一个例子:
# 代码实现
## 平衡因子
总结:
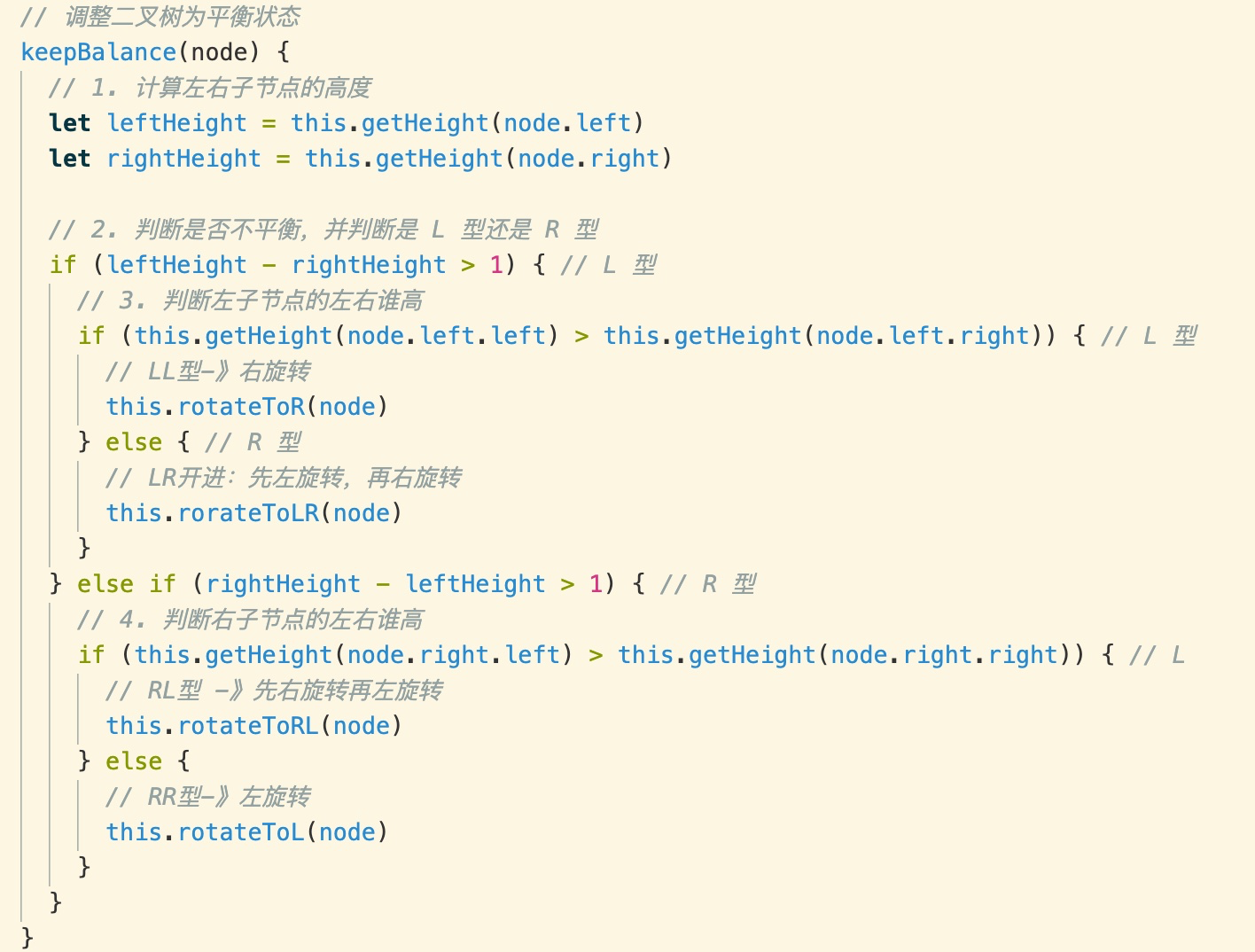
1. 平衡因子:左子树的高度-右子树的高度
2. 如果平衡因子大于等于 2 说明这个节点不平衡
3. 如果平衡因子是正数,说明:L 型(左高)
4. 如果平衡因子是负数,说明:R 型(右高)
## 获取一个的高度
节点高度:左右节点中到叶子节点最多的边数。
~~~
// 获取节点高度
getHeight(node) {
if(node === null) return 0
// 左右节点中最长的边数
return Math.max(this.getHeight(node.left), this.getHeight(node.right)) + 1
}
~~~
## 添加四种旋转方法
### 左旋
代码:

### 右旋
代码:

### 先左后右
代码:

### 先右后左
代码:

### 调整二叉树
计算一个节点的高度并判断是否平衡,如果不平衡,就判断是什么型并进行相应的旋转以保持平衡:
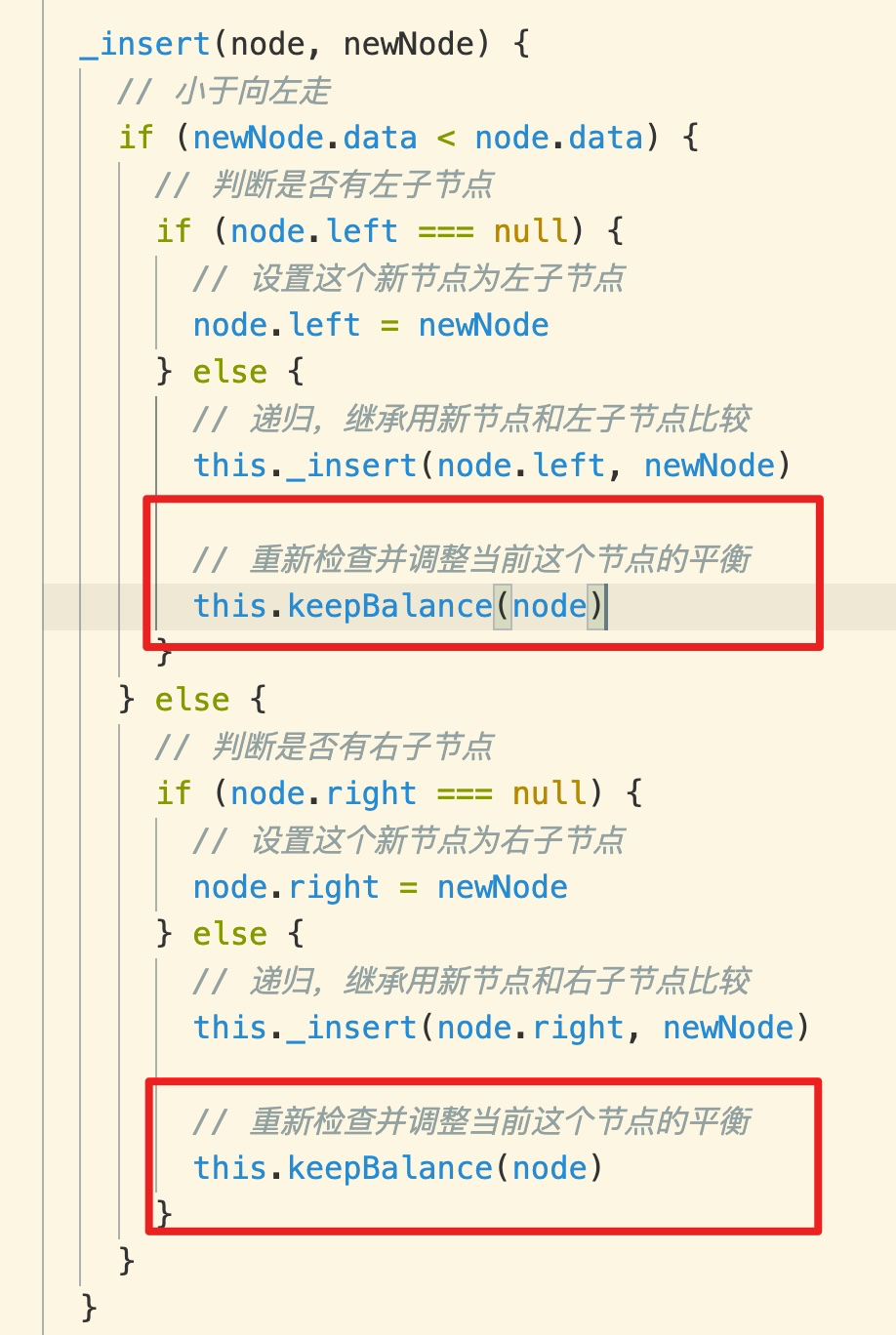
### 在添加节点时检查并调整节点
在每次添加一个新节点时,都有可能打破平衡,需要检查并调整:
修改添加节点的代码,在向儿子节点中添加节点时要重新检查并调整
# 完整 AVL Tree 代码
~~~
// 定义节点类
class Node {
constructor(data) {
this.data = data // 数据
this.left = null // 左子节点
this.right = null // 右子节点
}
}
// AVL树(自平衡二叉搜索树)
class AVLTree {
constructor() {
this.root = null // 根节点
this.length = 0 // 树中节点的数量
}
// 向树中插入一条记录
insert(data) {
// 1. 创建新的节点
let newNode = new Node(data)
// 2.放到树中
// 如果是空树
if (this.root === null) {
// 设置这个新节点为树根
this.root = newNode
} else {
// 从根节点开始比较
this.root = this._insert(this.root, newNode)
}
}
_insert(node, newNode) {
if (node === null) {
node = newNode
return node
}
// 小于向左走
if (newNode.data < node.data) {
// 判断是否有左子节点
if (node.left === null) {
// 设置这个新节点为左子节点
node.left = newNode
} else {
// 递归,继承用新节点和左子节点比较
node.left = this._insert(node.left, newNode)
// 重新检查并调整当前这个节点的平衡
node = this.keepBalance(node)
}
} else {
// 判断是否有右子节点
if (node.right === null) {
// 设置这个新节点为右子节点
node.right = newNode
} else {
// 递归,继承用新节点和右子节点比较
node.right = this._insert(node.right, newNode)
// 重新检查并调整当前这个节点的平衡
node = this.keepBalance(node)
}
}
return node
}
// 判断树中是否包含某一个数
has(data) {
// 从根节点开始查找
return this._has(this.root, data)
}
_has(node, data) {
// 如果节点为空,说明树中没有这个数
if (node == null) {
return false
}
// 如果值和前节点值相同,找到了
if (data == node.data) {
return true
} else if (data < node.data) {
// 到左子树中查找
return this._has(node.left, data)
} else if (data > node.data) {
// 到右子树中查找
return this._has(node.right, data)
}
}
// 前序遍历(根左右)
preOrder() {
this._preOrder(this.root)
}
// 开始的节点
_preOrder(node) {
if (node === null) return
// 根
console.log(node.data)
// 左
this._preOrder(node.left)
// 右
this._preOrder(node.right)
}
// 中序遍历(左根右)
midOrder() {
this._midOrder(this.root)
}
// 开始的节点
_midOrder(node) {
if (node === null) return
// 左
this._midOrder(node.left)
// 根
console.log(node.data)
// 右
this._midOrder(node.right)
}
// 后序遍历(左右根)
postOrder() {
this._postOrder(this.root)
}
// 开始的节点
_postOrder(node) {
if (node === null) return
// 左
this._postOrder(node.left)
// 右
this._postOrder(node.right)
// 根
console.log(node.data)
}
// 层序遍历
layerOrder() {
// 1. 创建一个队列(先入先出)
let queue = []
// 2. 先根节点放到队尾
queue.push(this.root)
// 3. 循环队列
let node
while (queue.length > 0) {
// 4. 从队头取出节点
node = queue.shift()
// 5. 左右子节点放入队尾
if (node.left !== null) queue.push(node.left)
if (node.right !== null) queue.push(node.right)
// 6. 输出当前节点(使用这个节点)
console.log(node.data)
}
}
// 获取节点高度
getHeight(node) {
if (node === null) return 0
// 左右节点中最长的边数
return Math.max(this.getHeight(node.left), this.getHeight(node.right)) + 1
}
// 左旋转
rotateToL(node) {
// 1. 取出右子节点(C)
let tmp = node.right
// 2. 父节点指向右子节点的左子节点
node.right = tmp.left
// 3. 右子节点的左子节点指向父节点
tmp.left = node
// 4. 返回新的顶点
return tmp
}
// 右旋转
rotateToR(node) {
let tmp = node.left
node.left = tmp.right
tmp.right = node
return tmp
}
// 先左旋再右旋转
rorateToLR(node) {
// 让左子节点左旋转,并让旋转之后的顶点做为左子节点
node.left = this.rotateToL(node.left)
// 再让当前节点右旋转
return this.rotateToR(node)
}
// 先右旋转再左旋转
rotateToRL(node) {
// 让右子节点先右旋转,并用新的顶点做为右子节点
node.right = this.rotateToR(node.right)
// 当前节点左旋
return this.rotateToL(node)
}
// 调整二叉树为平衡状态
keepBalance(node) {
if(node === null) return node
// 1. 计算左右子节点的高度
let leftHeight = this.getHeight(node.left)
let rightHeight = this.getHeight(node.right)
// 2. 判断是否不平衡,并判断是 L 型还是 R 型
if (leftHeight - rightHeight > 1) { // L 型
// 3. 判断左子节点的左右谁高
if (this.getHeight(node.left.left) >= this.getHeight(node.left.right)) { // L 型
// LL型-》右旋转
node = this.rotateToR(node)
} else { // R 型
// LR开进:先左旋转,再右旋转
node = this.rorateToLR(node)
}
} else if (rightHeight - leftHeight > 1) { // R 型
// 4. 判断右子节点的左右谁高
if (this.getHeight(node.right.left) >= this.getHeight(node.right.right)) { // L
// RL型 -》先右旋转再左旋转
node = this.rotateToRL(node)
} else {
// RR型-》左旋转
node = this.rotateToL(node)
}
}
return node
}
// 删除数据
deleteNode(data) {
// 从根开始比较删除
this.root = this._deleteNode(this.root, data)
}
_deleteNode(node, data) {
// 没有子节点了,不用删除
if (node == null) return null
if (data < node.data) {
// 往左走
node.left = this._deleteNode(node.left, data)
// 重新调整节点的平衡
return this.keepBalance(node)
} else if (data > node.data) {
// 往右走
node.right = this._deleteNode(node.right, data)
// 重新调整节点 平衡
return this.keepBalance(node)
} else {
// 如果相等就是找到了节点位置 ,要删除当前节点
// 情况一、有两个子节点
if (node.left !== null && node.right !== null) {
// 取出右子节点
let tmp = node.right
// 找出最小的节点(最左边的分支)
while (tmp.left !== null) {
tmp = tmp.left
}
// 把最小的值赋给当前节点
node.data = tmp.data
// 从右分支中删除这个最小的节点
node.right = this._deleteNode(this.right, tmp.data)
// 重新调整平衡
node = this.keepBalance(node)
return node
} else {
// 情况二、没有子节点
if (node.left === null && node.right === null) {
node = null
return null
}
// 情况三、只有左节点
if (node.left !== null) {
// 左节点替换当前节点
node = node.left
return node
}
// 情况四、只有右节点
if (node.right !== null) {
// 右节点替换当前节点
node = node.right
return node
}
}
}
}
}
const avl = new AVLTree()
avl.insert(3)
avl.insert(2)
avl.insert(1)
avl.insert(4)
avl.insert(5)
avl.deleteNode(1)
console.log(avl.root)
~~~
