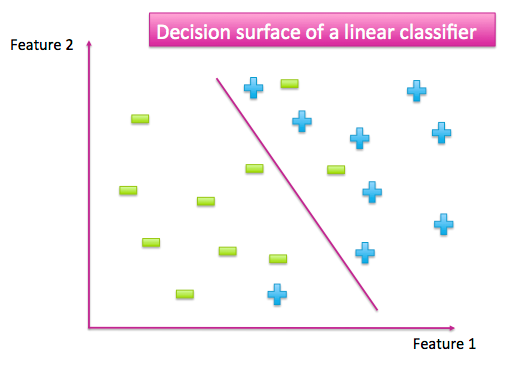
# 附录、线性模型和线性代数基 > 译者：[@Sherlock-kid](https://github.com/Sherlock-kid) ## 线性分类概述 当我们有一个已经标记的数据集时，特征空间散布着来自不同类别的数据点。分类器的工作是将不同类别的数据点分开。它可以通过生成一个数据点与另一个数据点非常不同的输出来实现。例如，当这里只有两个类别的时候，一个好的分类器应该为一个类别产生大量的输出，而另一个则为小的输出。作为一个类别而不是另一个类别的点就形成了一个决策平面。  图 A-1：简单的二元分类找到了一个分离两类数据点的曲面 许多函数能被当作分类器。这是一个寻找能完全分离不同类的简单函数的好方法。首先，相比于寻找最复杂的分类器，寻找最简单的分类器更容易。而且，简单函数常常能更好地适应新数据，要将它们与训练数据（特别是过度拟合）相比。一个简单的模型也许会出错，就像上图一些数据点被分到了错误的一边。但是我们牺牲了一些训练的准确性，以便有一个更简单的决策平面，可以达到更好的测试精度。最大限度减少复杂性和最大限度增加精度被叫做“奥卡姆剃刀”，广泛适用于科学与工程。 最简单的函数是一条直线。一个一元线性函数是我们最熟悉的。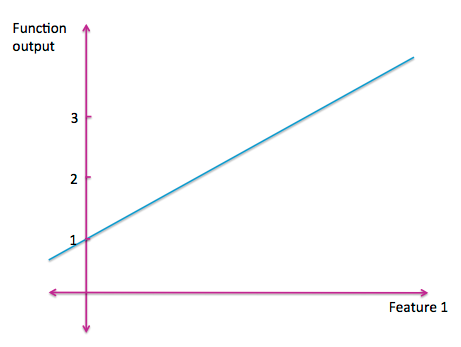  图 A-2：一元线性函数 二元线性函数可以显示为 3D 中的平面或 2D 中的等高线图（如图 A-3）。与拓扑地理图一样，等高线图的每一行代表输入空间中具有相同输出的点。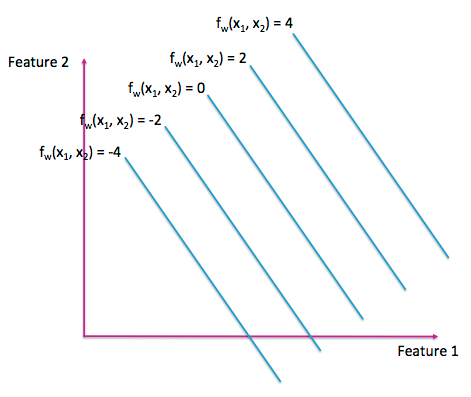  图 A-3：二维线性函数的等高线图 可视化更高维度的线性函数很难，它们被称作超平面。但是写出它们的代数公式还是很容易的。一个多维的线性模型有一个输入集合`x1,x2,…,xn`和一个权重参数集合`w0,w1,…,wn`：`fw(x1,x2,…,xn) = w0+w1*x1+w2*x2+…+wn*xn`。这个公式能被写成更简洁的向量形式 $fw(X)=X^T W$。 我们遵循通常的数学符号惯例，它使用粗体来表示一个向量和非粗体来表示一个标量。向量`x`在开始处用一个额外的 1 填充，作为截距项`w0`的占位符。如果所有输入特征都为零，那么函数的输出是`w0`。 所以`w0`也被称为偏差或截距项。 训练线性分类器相当于在类之间挑出最佳分离超平面。这意味着找到在空间中精确定位的最佳矢量`w`。由于每个数据点都有一个目标标签`y`，我们可以找到一个`w`，它试图直接模拟目标的标签 $x^T w=y$。 由于通常有多个数据点，我们需要一个`w`同时使所有的预测都接近目标标签： 方程 A-1：线性模型公式`Aw=y` 这里，`A`被称为数据矩阵（在统计中也被称为设计矩阵）。它包含特定形式的数据：每行是数据点，每列都是一个特征。（有时人们也会看到它的转置，其中的特征以行的形式显示，数据以列的形式显示。） ## 矩阵的解析 为了解决方程 A-1，我们需要一些线性代数的基本知识。为了系统地介绍这个主题，我们强烈推荐 Gilbert Strang 的书《Linear Algebra and Its Applications》（线性代数及其应用）。 方程 A-1 指出，当某个矩阵乘以某个向量时，会有一定的结果。一个矩阵也被叫做一个线性算子，这个名称使得矩阵更像一台小机器。该机器将一个矢量作为输入，并使用多个关键操作的组合来推导出另一个矢量：一个矢量方向的旋转，添加或减去维度，以及拉伸或压缩其长度。这种组合在输入空间中操纵形状时非常有用（见图 A-4）。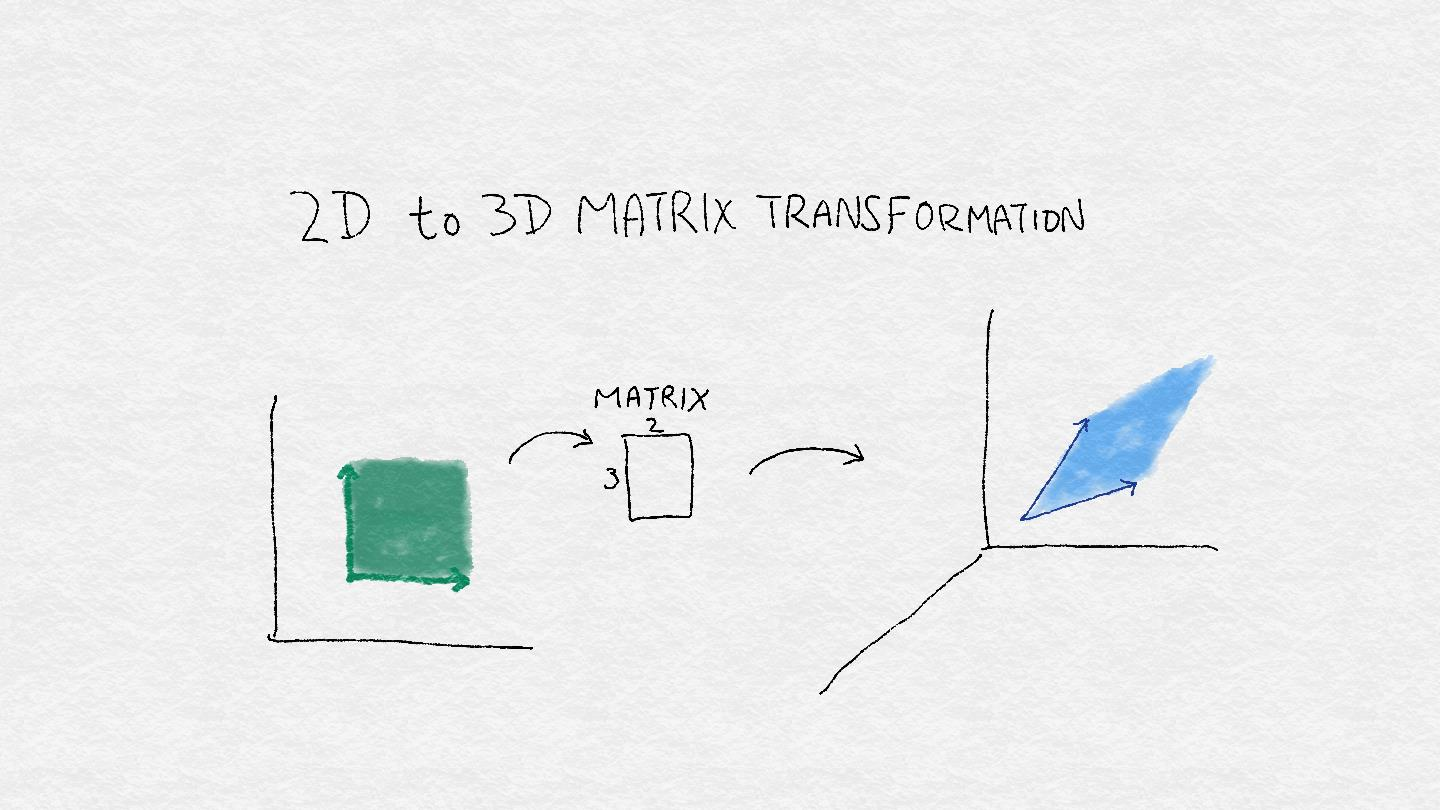  图 A-4：`3 x 2`矩阵可以将 2D 中的正方形区域转换为 3D 中的菱形区域。 它通过将输入空间中的每个向量旋转并拉伸到输出空间中的新向量来实现。 ## 从矢量到子空间 为了理解线性算子，我们必须看看它如何将输入变为输出。幸运的是，我们不必一次分析一个输入向量。向量可以组织成子空间，而线性算子则可以处理向量子空间。子空间是一组满足两个标准的向量：（1）如果它包含一个向量，那么它包含通过原点和该点的直线，以及（2）如果它包含两个点，则它包含所有线性组合 的这两个向量。 线性组合是两种操作类型的组合：将矢量与标量相乘，并将两个矢量相加在一起。 子空间的一个重要属性是它的秩或维度，它是这个空间中自由度的度量。一条线的秩为 1，2D 平面的秩为 2，依此类推。如果你可以想象在我们的多维空间中的多维鸟，那么子空间的秩告诉我们鸟可以飞行多少个“独立”的方向。这里的“独立”意思是“线性独立性”：如果一个不是另一个的常数倍，那么两个向量是线性独立的，即它们并不指向完全相同或相反的方向。 子空间可以被定义为一组基向量的范围。（跨度是描述一组向量的所有线性组合的技术术语。）一组向量的跨度在线性组合下是不变的（因为它是以这种方式定义的）。因此，如果我们有一组基向量，那么我们可以将这些向量乘以任何非零常数或者添加向量来获得另一个基。 有一个更独特和可识别的基来描述一个子空间将是很好的。标准正交基包含具有单位长度且彼此正交的矢量。正交性是另一个技术术语。（所有数学和科学中至少有50％是由技术术语组成的，如果你不相信我，请在本书中做一个袋装词）。如果两个向量的内积是 零。 对于所有密集的目的，我们可以将正交矢量看作相互成 90 度角。（这在欧几里得空间中是真实的，这与我们的物理三维现实非常相似。）将这些向量标准化为单位长度将它们变成一组统一的测量棒。 总而言之，一个子空间就像一个帐篷，正交基矢量是支撑帐篷所需的直角杆数。秩等于正交基向量的总数。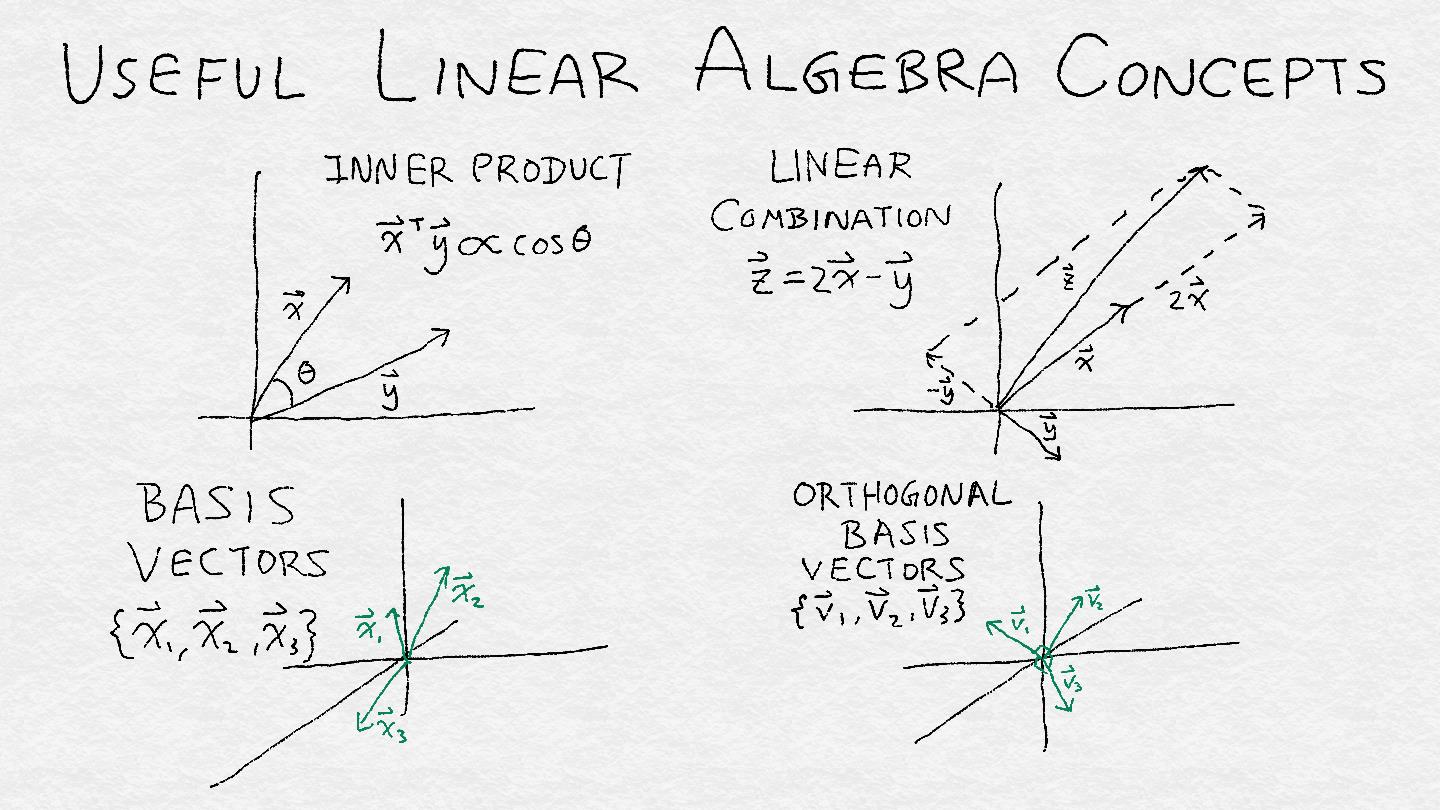  图 A-5：四个有用的线性代数概念的插图：内积，线性组合，基向量和正交基向量。 对于那些在数学中思考的人来说，这里有一些数学来描述我们的描述。 #### 有用的线性代数定义 + 标量：一个数`c`，不是矢量 + 向量：$x=(x_1,x_2,…,x_n)$ + 线性组合：$ax+by=ax_1+by_1,ax_2+by_2,…,ax_n+by_n$ + 向量组的范围：向量组 $u=a_1 v_1+⋯+a_k v_k$，$a_1,…,a_k$ 任意 + 线性独立性：`x`和`y`相互独立，如果`x≠cy`，`c`是任何标量常量 + 内在产品：$x,y=x_1 y_1+x_2 y_2+⋯+x_n y_n$ + 正交矢量：如果`x,y=0`，两个向量`x,y`正交 + 子空间：包含更大的矢量空间中的矢量子集，满足这三个标准： + 包含 0 向量 + 如果包含一个向量`v`，那么也包含所有向量`cv`，其中`c`是一个标量。 + 如果包含两个向量`u`和`v`，那么也包含`u+v` + 基：一组跨向子空间的向量 + 正交基：一个基 ${v_1,v_2,…,v_d}$，$v_i,v_j=0$，`i,j`任意 + 子空间的秩：跨越子空间的线性无关基向量的最小数目。 + ## 奇异值分解（SVD） 矩阵对输入向量执行线性变换。线性变换非常简单且受到限制。因此，矩阵不能无情地操纵子空间。线性代数最迷人的定理之一证明了每一个方阵，无论它包含什么数字，都必须将某一组矢量映射回自己，并进行一些缩放。在矩形矩阵的一般情况下，它将一组输入向量映射为相应的一组输出向量，其转置将这些输出映射回原始输入。技术术语是正方形矩阵具有特征值的特征向量，矩形矩阵具有奇异值的左右奇异向量。 #### 特征向量和奇异向量 设`A`是一个`n*n`的矩阵。如果这里有一个向量`v`和一个标量`λ`，使`Av=λv`，`v`称作特征向量，`λ`称为`A`的一个特征值。 让`A`成为一个长方形矩阵。如果这里有一个向量`u`和一个向量`v`和一个标量`σ`，那么`Av=σu`，$A^T u=σv$，`u`和`v`被叫做左右奇异向量，`σ`是`A`的奇异值。 代数上，矩阵的 SVD 看起来像这样： $A=U \Sigma V^T$ 其中矩阵`U`和`V`的列分别形成输入和输出空间的正交基。`Σ`是一个一个包含奇异值的对角矩阵。 在几何学上，矩阵执行以下的变换序列（见图 A-6）： + 将输入向量映射到右奇异向量基V上 + 通过相应的奇异值缩放每个坐标 + 将此分数与每个左奇异向量相乘 + 总结结果 当`A`是实矩阵（即所有元素都是实值）时，所有的奇异值和奇异向量都是实值的。奇异值可以是正数，负数或零。矩阵的有序奇异值集称为谱，它揭示了很多矩阵。奇异值之间的差距会影响解的稳定性，最大绝对奇异值与最小绝对奇异值之间的比值（条件数）会影响迭代求解器的求解速度。这两个属性都对可找到的解决方案的质量产生显着影响。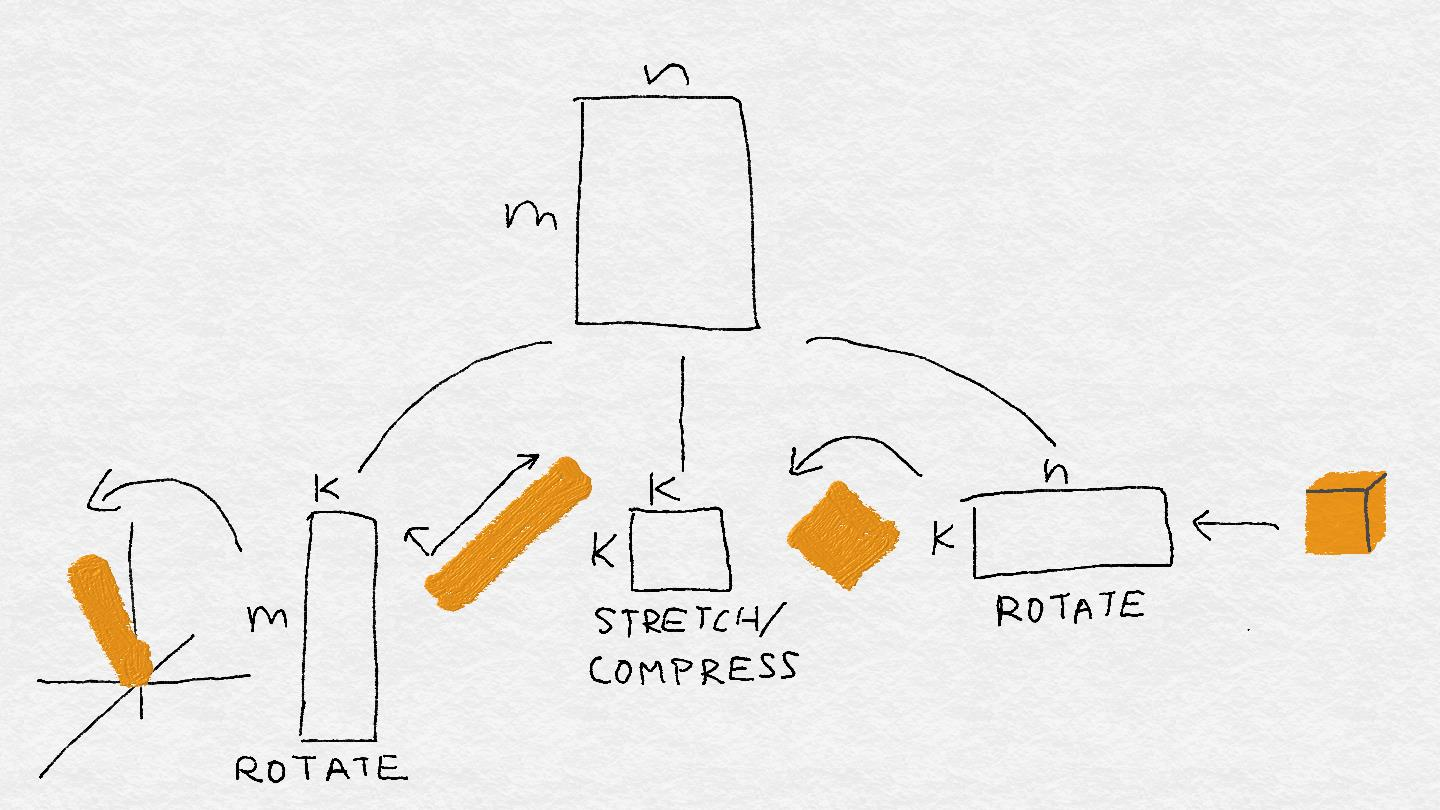  图 A-6：矩阵分解成三个小机器：旋转，缩放，旋转。 操作从右到左进行矩阵向量乘法。最右边的机器旋转并潜在地将输入投影到较低维空间中。在这个例子中，输入立方体变成了一个扁平的正方形，并且也被旋转了。下一台机器在一个方向挤压正方形，并将其拉伸到另一个方向；正方形变成矩形。最后一个最左边的机器再次旋转矩形，并将其投影回可能更高的空间。但它仍然是一个扁平的矩形，而不是一些更高维的对象。 ## 数据矩阵的四个基本子空间 解析矩阵的另一种有用方法是通过四个基本子空间：列空间，行空间，右空间和左空间。这四个子空间完全刻画了涉及`A`或 $A^T$ 的线性系统的解决方案。因此它们被称为四个基本子空间。对于数据矩阵，可以根据数据和特征理解四个基本子空间。让我们更详细地看看它们。 #### 数据矩阵 `A`：行是数据点，列是特征。 ### 列空间 数学定义： 当我们改变权值向量`w`时，输出向量`s`的集合，其中`s=Aw` 数学解释： 所有可能的列的组合。 数据解释： 根据观察到的特征，所有结果都是线性可预测的，向量`w`包含每个特征的权重。 基本原理： 对应非零奇异值的左奇异向量（`U`列的子集）。 ### 行空间 数学定义： 当我们改变权值向量`u`时，输出向量的集合 $r=u^T A$ 数学解释： 所有可能的行线性组合 数据解释： 行空间中的向量可以表示为现有数据点的线性组合。因此，这可以解释为已有数据的空间。向量`u`包含线性组合中每个数据点的权重。 基本原理： 对应非零奇异值的右奇异向量（`V`列的子集） ### 零空间 数学定义： 输入向量`w`的集合，其中`Aw=0`。 数学解释： 正交于`A`的所有行的向量。零空间被矩阵压缩为 0。这是“fluff”，它增加了`Aw=y`的解空间的体积。 数据解释： 新数据点，它不能被表示为现有数据点的任何线性组合 基本原理： 对应零奇异值的右奇异向量（`V`的其余列） ### 左零空间 数学定义： 输入向量`u`的集合，其中 $u^T A=0$ 数学解释： 正交于`A`的所有列的向量。左零空间正交于列空间。 数据解释： 不能用现有特征的线性组合来表示的新特征向量。 基本原理： 对应零奇异值的左奇异向量（`U`的其余列） 列空间和行空间包含根据观察到的数据和特性所能表示的内容。列空间中的这些向量是非新特征。那些位于行空间中向量都是非新的数据点。 对于建模和预测的目的，非新奇性是好的。完整的列空间意味着特征集包含足够的信息来建模我们的任何目标向量的愿望。一个完整的行空间意味着不同的数据点包含足够的变化来覆盖特性空间的所有可能的角落。我们要担心的是新的数据点和特征，它们分别包含在零空间和左零空间中。 在建立数据线性模型的应用，零空间中也可以看作是“新”数据点的子空间。在这种情况下，新奇并不是一件好事。新数据点是训练集不能线性表示的虚数据，同样，左零空间包含的新特征不能用现有特征的线性组合表示。 零空间正交于行空间。原因很简单，零空间的定义是`w`的内积为 0，每一个行向量都是`A`。因此，`w`正交于由这些行向量张成的空间即行空间。类似地，左零空间正交于列空间。 ### 求解一个线性系统 让我们把所有这些数学问题都归结到手头的问题上：训练一个线性分类器，它与解决线性系统的任务密切相关。我们仔细看一个矩阵是如何运作的，因为我们要逆向设计它。为了建立一个线性模型，我们必须找到输入权向量`w`映射到观察到的输出目标`y`在系统`Aw=y`，其中`A`是数据矩阵。让我们试着把线性算子的机器反过来转动。如果我们有`A`的 SVD 分解，那么我们可以把`y`映射到左奇异向量（`U`的列），反转比例因子（乘以非零奇异值的逆）最后把它们映射回正确的奇异向量（`V`的列），很简单，是吧？ 这实际上是计算`a`的伪逆的过程，它利用了一个标准正交基的一个关键性质：转置就是逆。这就是 SVD 如此强大的原因。（在实践中，真正的线性系统求解器不使用 SVD，因为它们计算是相当昂贵。还有其他更便宜的方法来分解矩阵，比如 QR、LU 或乔列斯基分解）。 然而，我们在匆忙中漏掉了一个小细节。如果奇异值为零会怎样？我们不能取零为倒数，因为`1/0=∞`。这就是为什么它叫伪逆。（矩形矩阵没有真实逆的定义，只有方阵（只要所有特征值非零）。无论输入什么，它的奇异值都为零；没有办法重新跟踪它的步骤并得出原始的输入。 好吧，让我们倒回来看这个小细节。让我们带着我们学到的，再往前走看看能不能把机器拆开。假设我们得到了`Aw=y`的答案，我们称它为特定的`w`，因为它特别适合`y`。假设还有一堆输入向量`A`被压到 0。让我们选一个，称它为 Wsad-trumpet。因为wah。那么当我们把 Wparticular 添加到 Wsad-trumpet，您认为会发生什么呢？ ``` A(Wparticular + Wsad-trumpet) = y ``` 神奇！这也是一个解。事实上，任何被压缩到零的输入都可以被添加到一个特定的解中，并解决方案是这样的： ``` Wgeneral = Wparticular + Whomogeneous ``` Wparticular 是方程`Aw=y`的精确解，可能有也可能没有这样的解。如果没有，那么系统只能近似地解决。如果有，那么`y`属于已知的`a`的列空间，列空间是`A`可以映射到的向量集合，通过它的列的线性组合。 Whomogeneous 是方程`Aw = 0`的解。（Wsadd-trumpet 的完整名称是“Whomogeneous”。）这一点现在应该很熟悉了。所有的广义向量的集合构成了`a`的零空间，这是具有奇异值为 0 的右奇异向量张成的空间。 “零空间”这个名字听起来像是一场生死攸关的危机的结局。如果零空间包含除零向量之外的任何向量，那么就有方程`Aw = y`有无穷多个解，有太多的解可供选择 来自本身并不是一件坏事。有时任何解决方案都可以。 但是如果有许多可能的答案，那么就有许多对分类任务有用的特性集。很难理解哪些是真正重要的。 解决大零空间问题的一种方法是通过添加来调节模型 额外的约束: Aw = y，其中ww = c 这种正则化形式使得权向量具有一定的范数。这种正则化的强度是由正则化参数控制的，正则化参数必须进行调整，就像我们在实验中所做的那样。 一般来说，特性选择方法处理选择最有用的特性来减少计算负担，减少模型的混乱程度，并使学习的模式更独特。这是“特性选择”的重点。 另一个问题是数据矩阵的“不均匀性”。当我们训练一个线性分类器时，我们不仅关心线性系统有一个通解，而且关心我们能轻易地找到它。通常，训练过程使用一个求解器，它通过计算损失函数的梯度和以小步骤下坡来工作。当某些奇异值非常大，而另一些非常接近于零时，求解者需要仔细地遍历较长的奇异向量(那些对应于较大奇异值的向量)，并花费大量时间挖掘较短的奇异向量以找到真正的答案。在光谱中这种“不均匀性”是由矩阵的条件数来衡量的，它基本上是最大和最小绝对值之间的比值。 综上所述，为了有一个相对独特的好的线性模型，为了让它容易被发现，我们希望: 1、标签向量可以通过特征子集(列向量)的线性组合很好地逼近。更好的是，特性集应该是线性无关的。 2、为了使零空间很小，行空间必须很大。(这是因为这两个子空间是正交的。)数据点(行向量)的集合越线性无关，零空间就越小。 •为了便于求解，数据矩阵的条件数——最大奇异值与最小奇异值之比——应该很小。 ## 分类器的概述 使用统计分类或分类器的方法来识别一个或者一组新的观察将属于哪个类别。书中引用的大多数方法都属于监督学习领域，在监督学习中，分类是通过使用预先确定的类别标记的训练数据进行算法确定的。我们将在这里给出这些算法的高级视图，仅仅足以理解它们在文本中的应用。(实际上，维基百科是你最好的朋友，因为它在每一种方法中都能找到很好的参考文献。) ### 支持向量机的径向基函数核 支持向量机径向基函数核(RBF SVM) 在Scikit Learn的sklearn.gaussian_process.kernes.RBF包 ### K-最近邻 K-最近邻(kNN) Scikit Learn的sklearn-neighbors包 ### 随机森林 随机森林（RF） 随机森林分类器在Scikit Learn的sklearn.ensembles包中 ### 梯度提升树 梯度提升树（GBT） 梯度提升树分类器在Scikit Learn的 sklearn.ensembles包中 严格地说，这里给出的公式是线性回归，而不是线性分类。不同的是，回归允许实值目标变量，而分类目标通常是表示不同类的整数。一个回归子可以通过非线性的变换转化为一个分类器。例如，logistic回归分类器通过logistic函数传递输入的线性变换。这些模型被称为广义线性模型，其核心是线性函数。虽然这个例子是关于分类的，但是我们使用线性回归公式作为教学工具，因为它更容易分析。直觉容易映射到广义线性分类器 实际上，它比那要复杂一些。$y$可能不在它的列空间中，所以这个方程可能没有解。统计机器学习不是放弃，而是寻找一个近似的解决方案。它定义了一个量化解决方案质量的损失函数。如果解是精确的，那么损失是0。小错误,小损失;大错误，大损失等等。然后，训练过程寻找最佳参数来最小化这个损失函数。在普通线性回归中，损失函数称为平方剩余损失，它本质上是将$y$映射到列空间中$A$的最近点。逻辑回归最小化了日志丢失。在这两种情况下，以及一般的线性模型中，线性系统$Aw = y$通常位于核心。因此，我们的分析是非常相关的。