# 七、物理建模
> 原文:[Chapter 7 Physical modeling](http://greenteapress.com/complexity2/html/thinkcomplexity2008.html)
> 译者:[飞龙](https://github.com/wizardforcel)
> 协议:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
> 自豪地采用[谷歌翻译](https://translate.google.cn/)
到目前为止,我们所看到的细胞自动机不是物理模型;也就是说,他们不打算描述现实世界中的系统。 但是一些 CA 用作物理模型。
在本章中,我们考虑一个 CA,它模拟扩散(散开)并相互反应的化学物质,这是 Alan Turing 提出的过程,用于解释一些动物模式如何发展。
我们将试验一种 CA,它模拟通过多孔材料的渗透液体,例如通过咖啡渣的水。 这个模型是展示相变行为和分形几何的几个模型中的第一个,我将解释这两者的含义。
本章的代码位于本书仓库的`chap07.ipynb`中。 使用代码的更多信息,请参见第?节。
## 7.1 扩散
1952 年,艾伦图灵发表了一篇名为“形态发生的化学基础”的论文,该论文描述了涉及两种化学物质的系统行为,它们在空间中扩散并相互反应。 他表明,这些系统根据扩散和反应速率产生了广泛的模式,并推测像这样的系统可能是生物生长过程中的重要机制,特别是动物着色模式的发展。
图灵模型基于微分方程,但也可以使用细胞自动机来实现。
但在我们开始使用图灵模型之前,我们先从简单的事情开始:只有一种化学物质的扩散系统。 我们将使用 2-D CA,其中每个细胞的状态是连续的数量(通常在 0 和 1 之间),表示化学物质的浓度。
我们将通过比较每个细胞与其邻居的均值,来建模扩散过程。 如果中心细胞的浓度超过领域均值,则化学物质从中心流向邻居。 如果中心细胞的浓度较低,则化学物质以另一种方式流动。
以下核计算每个细胞与其邻居均值之间的差异:
```py
kernel = np.array([[0, 1, 0],
[1,-4, 1],
[0, 1, 0]])
```
使用`np.correlate2d`,我们可以将这个核应用于数组中的每个细胞:
```py
c = correlate2d(array, kernel, mode='same')
```
我们将使用一个扩散常数`r`,它关联了浓度差与流速:
```py
array += r * c
```
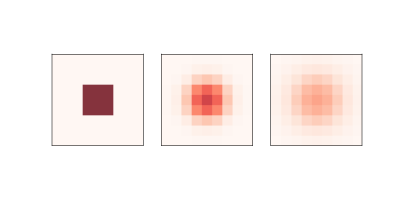
图 7.1:0,5 和 10 步后的简单扩散模型
图?显示 CA 的结果,其中`n=9, r=0.1`,除了中间的“岛”外,初始浓度为 0。 该图显示了 CA 的启动状态,以及 5 步和 10 步之后的状态。 化学物质从中心向外扩散,直到各处浓度相同。
## 7.2 反应扩散
现在我们添加第二种化学物。 我将定义一个新对象`ReactionDiffusion`,它包含两个数组,每个化学物对应一个:
```py
class ReactionDiffusion(Cell2D):
def __init__(self, n, m, params):
self.params = params
self.array = np.ones((n, m), dtype=float)
self.array2 = np.zeros((n, m), dtype=float)
island(self.array2, val=0.1, noise=0.1)
```
`n`和`m`是数组中的行数和列数。 `params`是参数元组,下面我会解释它。
数组代表第一种化学物质`A`的浓度,它最初是无处不在的。
`array2`表示`B`的浓度,除了中间的一个岛屿,它初始为零,并且由`island`初始化:
```py
def island(a, val, noise):
n, m = a.shape
r = min(n, m) // 20
a[n//2-r:n//2+r, m//2-r:m//2+r] = val
a += noise * np.random.random((n, m))
```
岛的半径`r`是`n`或`m`的二十分之一,以较小者为准。 岛的高度是`val`,在这个例子中是`0.1`。 此外,随机均匀噪声(值为 0 到`noise`)添加到整个数组。
这里是更新数组的`step `函数:
```py
def step(self):
"""Executes one time step."""
A = self.array
B = self.array2
ra, rb, f, k = self.params
cA = correlate2d(A, self.kernel, **self.options)
cB = correlate2d(B, self.kernel, **self.options)
reaction = A * B**2
self.array += ra * cA - reaction + f * (1-A)
self.array2 += rb * cB + reaction - (f+k) * B
```
参数是
`ra`:
`A`的扩散速率(类似于前一节中的`r`)。
`rb`:
`B`的扩散速率。在该模型的大多数版本中,`rb`约为`ra`的一半。
`f`:
进给速率,控制着`A`添加到系统的速度。
`k`:
移除速率,控制`B`从系统中移除的速度。
现在让我们仔细看看更新语句:
```py
reaction = A * B**2
self.array += ra * cA - reaction + f * (1-A)
self.array2 += rb * cB + reaction - (f+k) * B
```
数组`cA`和`cB`是将扩散核应用于`A`和`B`的结果。乘以`ra`和`rb`得出进入或离开每个细胞的扩散速率。
表达式`A * B ** 2`表示`A`和`B`相互反应的比率。 假设反应消耗`A`并产生`B`,我们在第一个方程中减去这个项并在第二个方程中加上它。
表达式`f * (1-A)`决定`A`加入系统的速率。 当`A`接近 0 时,最大进给速率为`f`。 当`A`接近 1 时,进给速率下降到零。
最后,表达式`(f+k) * B`决定`B`从系统中移除的速率。 当`B`接近 0 时,该比率变为零。
只要速率参数不太高,`A`和`B`的值通常保持在 0 和 1 之间。

图 7.2:1000,2000 和 4000 步之后的反应扩散模型,参数为`f=0.035`和`k=0.057`
使用不同的参数,该模型可以产生类似于各种动物身上的条纹和斑点的图案。 在某些情况下,相似性是惊人的,特别是当进给和移除参数在空间上变化时。
对于本节中的所有模拟,`ra = 0.5`,`rb = 0.25`。
图?显示了`f=0.035`和`k=0.057`的结果,`B`的浓度以较暗的颜色显示。 有了这些参数,系统就向稳定状态演化,在`B`的黑色背景上有`A`的光点。
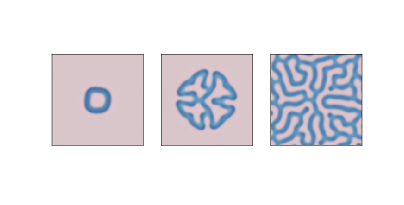
图 7.3:1000,2000 和 4000 步之后的反应扩散模型,参数为`f=0.055`和`k=0.062`
图?显示了`f = 0.055`和`k = 0.062`的结果,在`A`的背景上产生了珊瑚样的`B`。
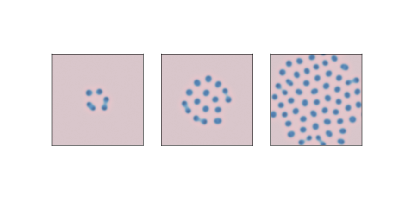
图 7.4:1000,2000 和 4000 步之后的反应扩散模型,参数为`f=0.039`和`k=0.065`
图?显示了`f = 0.039`和`k = 0.065`的结果。 在类似于有丝分裂的过程中,这些参数产生的`B`点生长和分裂,最后形成稳定的等距点图案。
1952 年以来,观察和实验为图灵猜想提供了一些支持。 目前为止,看起来许多动物图案实际上由某种反应扩散过程形成,但尚未证实。
## 7.3 渗流
渗流是流体流过半多孔材料的过程。 实例包括岩层中的油,纸中的水和微孔中的氢气。 渗流模型也用于研究不是严格渗滤的系统,包括流行病和电阻网络。 请见 <http://en.wikipedia.org/wiki/Percolation_theory>。
渗流模型常常用随机图来表示,就像我们在第?章中看到的那样,但它们也可以用细胞自动机表示。 在接下来的几节中,我们将探索模拟渗流的 2-D CA。
在这个模型中:
+ 最初,每个细胞是概率为`p`的“多孔”或者“无孔”,并且除了顶部那行是“湿的”之外,所有单元都是“干的”。
+ 在每个时间步骤中,如果多孔细胞至少有一个湿的邻居,它会变湿。 非多孔细胞保持干燥。
+ 模拟运行直至达到不再有细胞改变状态的“固定点”。
如果存在从顶部到底部的湿细胞路径,我们说 CA 具有“渗流簇”。
渗流的一个主要问题是,找到渗流簇的概率以及它如何依赖于`p`。 这个问题可能会让你想起第?节,其中我们计算了随机 ER 图连接的概率。 我们会看到这两个模型之间的几个关系。
我定义了一个新类来表示渗流模型:
```py
class Percolation(Cell2D):
def __init__(self, n, m, p):
self.p = p
self.array = np.random.choice([0, 1], (n, m), p=[1-p, p])
self.array[0] = 5
```
`n`和`m`是 CA 中的行数和列数。 `p`是细胞为多孔的概率。
CA 的状态存储在数组中,该数组使用`np.random.choice`初始化,以概率`p`选择 1(多孔),以概率`1-p`选择 0(无孔)。 顶部那行的状态设置为 5,表示一个湿细胞。
在每个时间步骤中,我们使用 4 细胞邻域(不包括对角线)来检查任何多孔细胞是否拥有湿的邻居。 这是核:
```py
kernel = np.array([[0, 1, 0],
[1, 0, 1],
[0, 1, 0]])
```
这里是`step `函数:
`correlate2d`将邻居的状态相加,如果至少有一个邻居是湿的,那么至少大于 5。 最后一行寻找多孔的细胞,`a == 1`,并且至少有一个湿邻居,`c >= 5`,并将它们的状态设置为 5,这代表湿的。

图 7.5:渗流模型的前三个步骤,其中`n=10`和`p=0.5`
图?显示了`n = 10`和`p = 0.5`的渗流模型的前几个步骤。 非多孔细胞为白色,多孔细胞为浅色,湿细胞为深色。
## 7.4 相变
现在让我们测试 CA 是否包含渗流簇。
```py
def test_perc(perc):
num_wet = perc.num_wet()
num_steps = 0
while True:
perc.step()
num_steps += 1
if perc.bottom_row_wet():
return True, num_steps
new_num_wet = perc.num_wet()
if new_num_wet == num_wet:
return False, num_steps
num_wet = new_num_wet
```
`test_perc`接受`Percolation`对象作为参数。 每次循环中,它都会使 CA 前进一个时间步骤。 它检查底部那行,看看有没有湿的细胞;如果有,它返回`True`,表示存在渗透簇,以及`num_steps`,它是到达底部所需的时间步数。
在每个时间步骤中,它还计算湿细胞的数量并检查自上一步以来数量是否增加。 如果没有,我们已经到达了固定点,而没有找到一个渗流簇,所以我们返回`False`。
为了估计渗流簇的概率,我们生成许多随机初始状态并测试它们:
```py
def estimate_prob_percolating(p=0.5, n=100, iters=100):
count = 0
for i in range(iters):
perc = Percolation(n, p=p)
flag, _ = test_perc(perc)
if flag:
count += 1
return count / iters
```
`estimate_prob_percolating`使用给定的`p`和`n`值生成 100 个 CA,并调用`test_perc`来查看其中有多少个具有渗流簇。 返回值是拥有的 CA 的比例。
当`p = 0.55`时,渗滤簇的概率接近于 0。`p = 0.60`时,它约为 70%,而在`p = 0.65`时,它接近于 1。这种快速转变表明`p`的临界值接近 0.6。
我们可以更精确地使用随机游走来估计临界值。 从`p`的初始值开始,我们构造一个`Percolation`对象并检查它是否具有渗透簇。 如果是这样,`p`可能太高,所以我们减少它。 如果不是,`p`可能太低,所以我们增加它。
这里是代码:
```py
def find_critical(p=0.6, n=100, iters=100):
ps = [p]
for i in range(iters):
perc = Percolation(n=n, p=p)
flag, _ = test_perc(perc)
if flag:
p -= 0.005
else:
p += 0.005
ps.append(p)
return ps
```
`find_critical`以`p`的给定值开始并上下调整,返回值的列表。 当`n = 100`时,`ps`的平均值约为 0.59,对于从 50 到 400 的`n`值,这个临界值似乎是一样的。
临界值附近的行为的快速变化称为相变,类似于物理系统中的相变,例如水在冰点处从液体变为固体的方式。
在处于或接近临界点时,各种各样的系统展示了一组共同的行为和特征。这些行为被统称为临界现象。 在下一节中,我们将探究其中的一个:分形几何。
## 7.5 分形
为了理解分形,我们必须从维度开始。
对于简单的几何对象,维度根据缩放行为而定义。 例如,如果正方形的边长为`l`,则其面积为`l ** 2`。 指数 2 表示正方形是二维的。 同样,如果立方体的边长为`l`,则其体积为`l ** 3`,这表示立方体是三维的。
更一般来说,我们可以通过测量一个对象的“尺寸”(通过一些定义),将对象的维度估计为线性度量的函数。
例如,我将通过测量一维细胞自动机的面积(“开”细胞的总数),将它的维度估计为行数的函数。
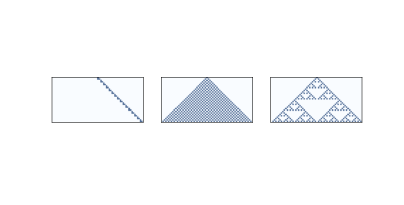
图 7.6:32 个时间步之后,规则为 20,50 和 18 的一维 CA。
图?展示了三个一维 CA,就像我们在第?节中看到的那样。 规则 20(左)产生一组看似线性的细胞,所以我们预计它是一维的。 规则 50(中)产生类似于三角形的东西,所以我们预计它是二维的。 规则 18(右)也产生类似三角形的东西,但密度不均匀,所以其缩放行为并不明显。
我将用以下函数来估计这些 CA 的维度,该函数计算每个时间步之后的细胞数。 它返回一个元组列表,其中每个元组包含`i`和`i ** 2`,用于比较,以及细胞总数。
```py
def count_cells(rule, n=500):
ca = Cell1D(rule, n)
ca.start_single()
res = []
for i in range(1, n):
cells = np.sum(ca.array)
res.append((i, i**2, cells))
ca.step()
return res
```
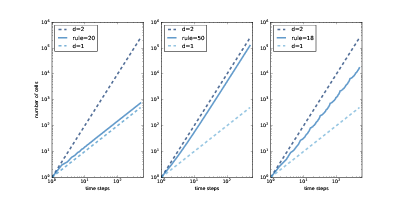
图 7.7:规则 20,50 和 18 的“开”细胞的数量与时间步数。
图?展示以双对数刻度绘制的结果。
在每幅图中,顶部虚线表示`y = i ** 2`。 两边取对数,我们得到`logy = 2logi`。 由于该数字在双对数刻度上,因此直线的斜率为2。
同样,底部的虚线表示`y = i`。 在双对数刻度上,直线的斜率为 1。
规则 20(左)每两个时间步骤产生三个细胞,所以`i`步后的细胞总数为`y = 1.5 i`。 两边取对数,我们得到`logy = log1.5 + logi`,所以在双对数刻度上,我们期待一条斜率为 1 的线。实际上,线的估计的斜率为 1.01。
规则 50(中)在第`i`个时间步骤中产生`i + 1`个新细胞,因此`i`步之后的细胞总数为`y = i ** 2 + i`。 如果我们忽略第二项并取两边的对数,我们有`logy ~ 2 logi`,所以当`i`变大时,我们预计看到一条斜率为 2 的线。事实上,估计的斜率为 1.97。
最后,对于规则 18(右),估计的斜率大约是 1.57,这显然不是 1,2 或任何其他整数。 这表明规则 18 生成的图案具有“分数维度”;也就是说,它是一个分形。
## 7.6 分形和渗流模型

图 7.8:`p=0.6`和`n=100, 200, 300`的渗流模型
现在让我们回到渗透模型。 图?展示了`p = 0.6`和`n = 100, 200, 300`的渗流模型中的湿细胞簇。非正式来说,它们类似于在自然界和数学模型中看到的分形模式。
为了估计它们的分形维度,我们可以运行一系列尺寸的 CA,计算每个渗流簇中湿细胞的数量,然后看看随着我们增加 CA 的大小,细胞计数的规模如何增长。
以下循环运行了模拟:
```py
for size in sizes:
perc = Percolation(size, p=p)
flag, _ = test_perc(perc)
if flag:
num_filled = perc.num_wet() - size
res.append((size, size**2, num_filled))
```
结果是元组列表,其中每个元组包含`size `和`size ** 2`,用于比较,以及渗流簇中的细胞数(不包括顶行中的初始湿细胞)。
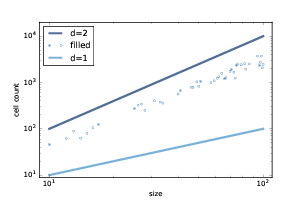
图 7.9:渗流簇中的细胞数量与 CA 大小
图?展示了 10 到 100 范围内的结果。点展示了每个渗流簇中的细胞数。 拟合这些点的线的斜率大约为 1.85,这表明当`p`接近临界值时,渗滤簇实际上是分形的。
当`p`大于临界值时,几乎每个多孔细胞都被填充,因此湿单元的数量仅为`p * size ** 2`,它的维度为 2。
当`p`远小于临界值时,湿细胞的数量与 CA 的线性大小成比例,因此它的维度为 1。
## 7.7 练习
练习 1
在第?节中,我们发现 CA 规则 18 产生了一个分形。 你能找到其他产生分形的一维 CA 吗?
注意:`Cell1D.py`中的`Cell1D`对象不会从左边绕到右边,对于某些规则它在边界上创建了手工艺品 [?]。你可能想要使用`Wrap1D`,它是`Cell1D`的子类。 它也在`Cell1D.py`中定义。
练习 2
1990 年,Bak,Chen 和 Tang 提出了一种细胞自动机,它是一种森林火灾的抽象模型。 每个细胞处于三种状态之一:空,被树占用或着火。
CA 的规则是:
+ 空细胞以概率`p`被占用。
+ 如果任何一个邻居着火,那么带有树的细胞就会燃烧。
+ 即使没有邻居着火,带有树的细胞自发燃烧,概率为`f`。
+ 在下一个时间步骤中,着火的细胞变为空细胞。
编写一个实现这个模型的程序。 你可能想要继承`Cell2D`。 参数的常用值为`p = 0.01`和`f = 0.001`,但你可能想要尝试其他值。
从随机初始条件开始,运行 CA 直到它达到稳定状态,树的数量不再持续增加或减少。
在稳定状态下,森林分形的几何形状是什么? 它的分形维度是多少?
