``` // 带记忆的递归:Fibonacci210802.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。// #include <iostream> #define Max1 1000001 int FaA[Max1]; //unsigned long long tmpn_1; int tmpn_1; int tmpn_2; //unsigned long long tmpn_2; //unsigned long long int Fibonacci(int n) { if (0 == n) return 0; if(2>n) return 1;// if (1 == n) return 1; // if (2 == n) return 1; // if (-1 != FaA[(n-1)]) { tmpn_1 = FaA[n - 1]; } else if (-1==FaA[n-1]) tmpn_1 = Fibonacci((n-1)); // 后面的语句是等价代码： tmpn_1 = (-1 == FaA[n - 1]) ? Fibonacci(n - 1) : FaA[n - 1]; //此句为前面代码的等价语句， //只不过此为 “三目”写法 tmpn_2 = (-1 == FaA[n - 2]) ? Fibonacci(n - 2) : FaA[n - 2]; // if (-1 != FaA[(n - 2) ]) { tmpn_2 = FaA[n - 2]; } else if (-1==FaA[n-2]) tmpn_2 = Fibonacci((n - 2) ); FaA[n] = tmpn_1 + tmpn_2; return ( FaA[n] ); }// int main() { int nn = 9; for (int i = 0; i < Max1; ++i) { FaA[i] = -1; } FaA[0] = 0; FaA[1] = 1; //unsigned long long int tmpull = Fibonacci(nn); for(int ii=0;ii<=nn;++ii ) {//for220i std::cout << "当N为:" << ii << "Fibonacci数为:"; std::cout << FaA[ii] << std::endl; }//for220i std::cout << "当N为:" << nn <<"Fibonacci数为:"; std::cout << tmpull << std::endl; std::cout << "Hello World!\n"; }//main ``` （程序的）**代码 都是写给 人类看的……，只不过是刚好计算机可以执行而已。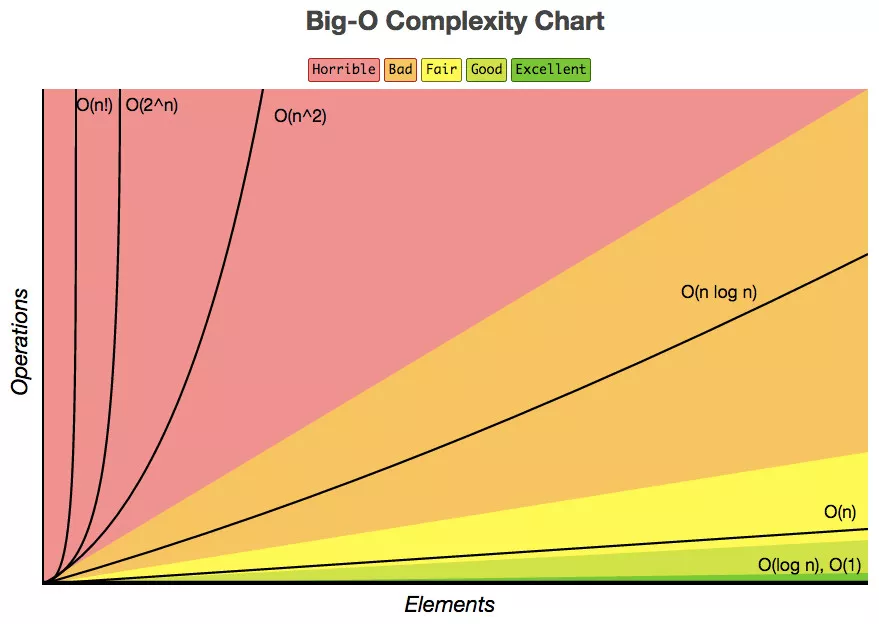**So，写代码既是技术活儿，也是艺术创作…… 前面程序的运行结果： 当N为:0Fibonacci数为:0 当N为:1Fibonacci数为:1 当N为:2Fibonacci数为:1 当N为:3Fibonacci数为:2 当N为:4Fibonacci数为:3 当N为:5Fibonacci数为:5 当N为:6Fibonacci数为:8 当N为:7Fibonacci数为:13 当N为:8Fibonacci数为:21 当N为:9Fibonacci数为:34 当N为:9Fibonacci数为:34  上图的，红份色部分的算法就可以称为“对付法”、对付算法…… 因为算法复杂度实在太高！