``` ## 举个例子 有两个桶，1号桶里有40个球，其中30个白球，10个黑球；2号桶里也有40个球，其中20个白球，20个黑球。 **先假设几个事件：** > A事件：抓取1个球，球来自1号桶。 > B事件：抓取的是白球。 > C事件：抓取1个球，球来自2号桶。 ## **条件概率/全概率/逆概率** ***条件概率：***从1号桶中抽取白球的概率P(B|A)=30/(30+10)=75%；从2号桶中抽取白球的概率P(B|C)=20/(20+20)=50%，这些都是条件概率。 ***全概率：***抽取一个球，为白球的概率，这个概率叫全概率，是1号桶中抽取白球和2号桶中抽取白球两个事件的概率之和，即 P(B)=P(B|A)P(A)+P(B|C)P(C)=75% \***50% + 50% \***50%= 62.5%。 ***逆概率/贝叶斯定理：***抓取了一个球是白球，那么这个白球来自1号桶的概率P(A|B)是多少，这就是典型的贝叶斯定理解决的问题。 ## 贝叶斯公式 P(A|B）如何求呢？这就用到贝叶斯公式了。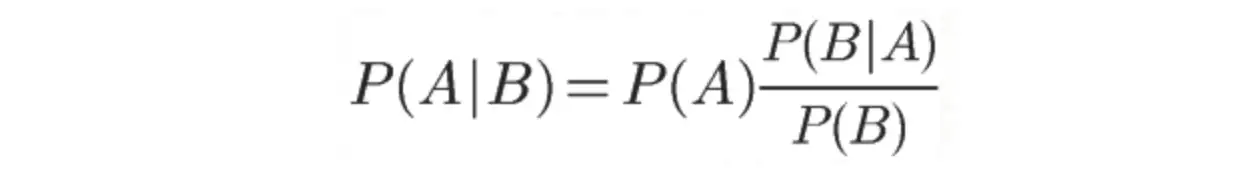  ## 如何使用贝叶斯定理？ 1\. 先求P(A），即抓取一个球，球来自A桶的概率，这叫做【先验概率】，也就是在没有约束条件（约束条件为抽取的是白球）下事件A发生的概率，这个很好计算为50%。 2\. 再求P(B|A)/P(B)，这叫做【可能性函数】或【调整函数】，也就是在已知条件下抓取的是白球的情况下，对P(A）进行调整的因子。根据上文计算的P(B|A）= 75%，P(B)= 62.5%，得出调整因子为75%/62.5%=1.2。 3\. 最后求P(A|B），也被叫做【后验概率】= 【先验概率】 \* 【调整函数】= P(A）**\* (P(B|A)/P(B)) = 50% \* 1.2 = 60% 。** 也就是说，抽取一个球，在信息不完整的情况下，这个球来自1号桶的概率为50%；在我们知道这个球是白球的条件下，那么这个球来自1号桶的可能性提高了20%（调整因子为1.2），则最终抽取的是白球且来自1号桶的概率将提升到60%。 **具体过程见下图：**  ```
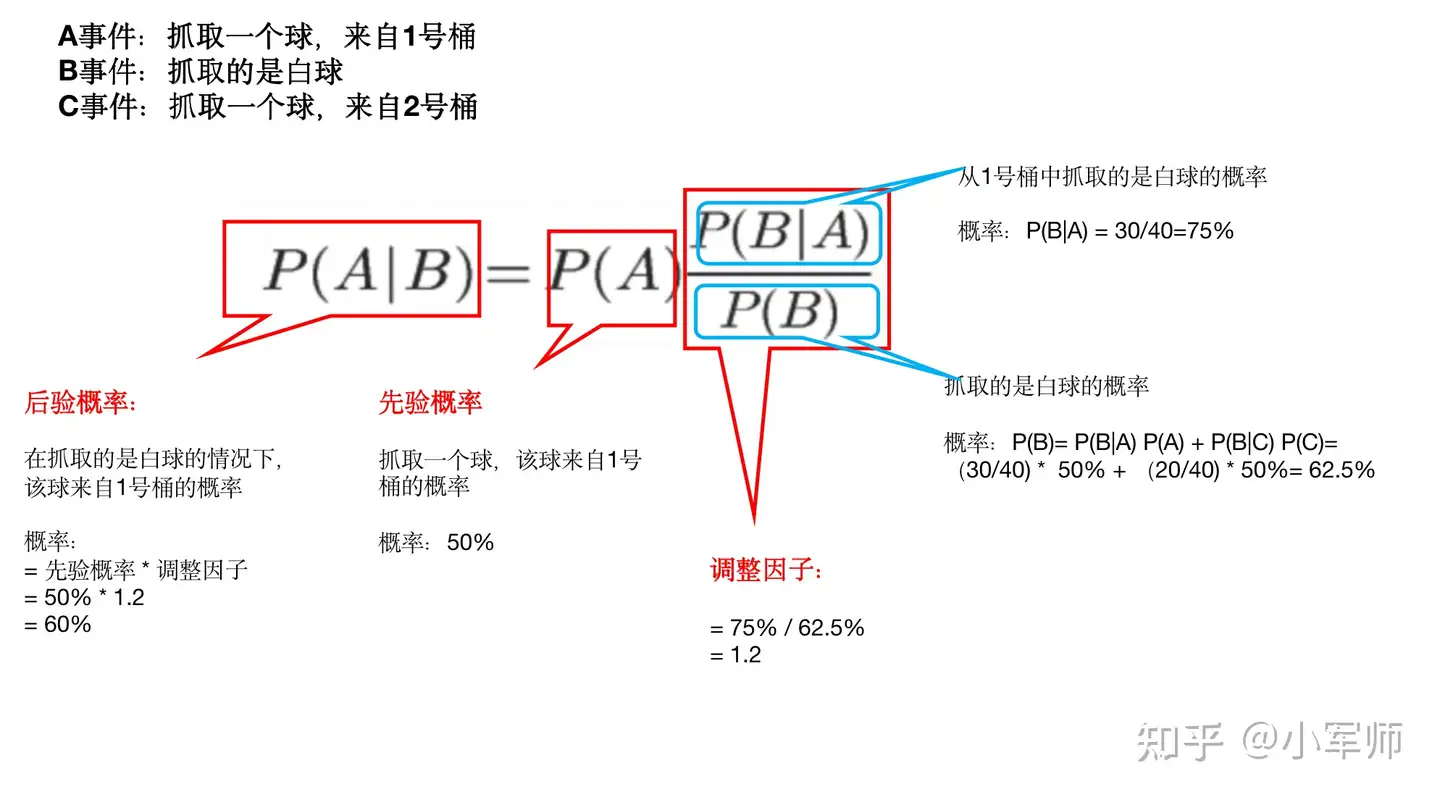