[TOC] # 什么是大O符号? **大O符号**（英语：Big O notation），又称为**渐进符号**，是用于描述[函数](https://zh.wikipedia.org/wiki/%E5%87%BD%E6%95%B0 "函数")[渐近行为](https://zh.wikipedia.org/wiki/%E6%B8%90%E8%BF%91%E5%88%86%E6%9E%90 "渐近分析")的[数学](https://zh.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6 "数学")符号。更确切地说，它是用另一个（通常更简单的）函数来描述一个函数[数量级](https://zh.wikipedia.org/wiki/%E6%95%B0%E9%87%8F%E7%BA%A7 "数量级")的**渐近上界**。在[数学](https://zh.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6 "数学")中，它一般用来刻画被截断的[无穷级数](https://zh.wikipedia.org/wiki/%E6%97%A0%E7%A9%B7%E7%BA%A7%E6%95%B0 "无穷级数")尤其是[渐近级数](https://zh.wikipedia.org/w/index.php?title=%E6%B8%90%E8%BF%91%E7%BA%A7%E6%95%B0&action=edit&redlink=1 "渐近级数（页面不存在）")的剩余项；在[计算机科学](https://zh.wikipedia.org/wiki/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%A7%91%E5%AD%A6 "计算机科学")中，它在[分析](https://zh.wikipedia.org/wiki/%E7%AE%97%E6%B3%95%E5%88%86%E6%9E%90 "算法分析")[算法](https://zh.wikipedia.org/wiki/%E7%AE%97%E6%B3%95 "算法")[复杂性](https://zh.wikipedia.org/wiki/%E8%A8%88%E7%AE%97%E8%A4%87%E9%9B%9C%E6%80%A7%E7%90%86%E8%AB%96 "计算复杂性理论")的方面非常有用。 大O符号/大 O 表示法 只是描述代码的性能如何取决于其处理的数据量的一种奇特的方式。 它允许我们计算一个算法可能的最坏运行时间，或者算法完成需要多长时间。 换句话说，它根据输入的大小告诉我们它会慢多少。 ~~~ T(n) = O(f(n)) S(n) = O(f(n)) ~~~ 这个叫做大 O 表示法，其中的 T 代表的是算法需要执行的总时间 * S 表示的算法需要的总空间 * f (n) 表示的是代码执行的总次数 它通常以两种方式来讨论**时间复杂度（Time Complexity）**(算法花费的时间)和**空间复杂度（Space Complexity）**(算法占用的空间)。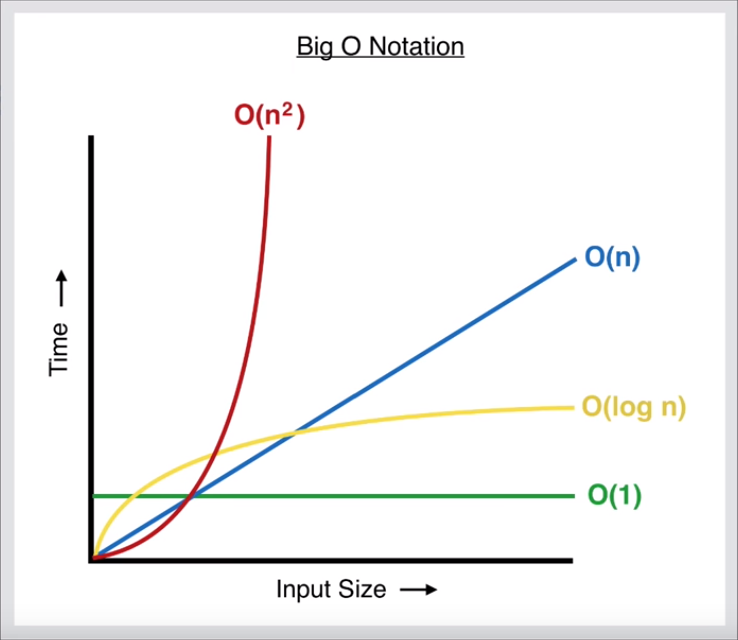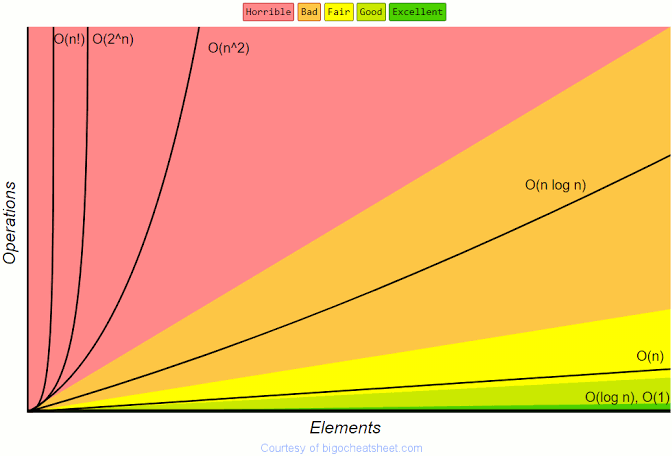 我把这个图放在这里，我们继续讨论时可以参考它，这张图显示了相互之间的复杂性。   # 时间复杂度 首先什么是时间复杂度，时间复杂度这个定义如果在之前没有接触过的话，你可能会认为他代表的是一个代码执行的时间，其实不然，算法的时间复杂度就是说一个算法的执行时间根据数据规模增长的一个趋势，并不是说代码执行的具体时间。 | 记号法| 名称 | 表情符号| 简短说明 | 详细的描述 | | --- | --- |--- |--- |--- |--- | | O(1) | 常量 | 😎 | 数据集的大小不影响运行速度 | 总是耗费相同的时间 | | O(log n) | 对数 | 😁 | 10x the data means 2x more time | 每次循环迭代后的工作量除以2。如 二分查找|对分查找（binary search） | | O(n) | 线性 | 😐 | 10x the data means 10x more time | 完成所需耗费的时间与输入数据大小成 `1:1` 的关系。 | | O(n log n) | 直线的（linearithmic） | 😟 | 10x the data means about 20x more time | 这是一个嵌套循环。其内部循环在 `log n` 时间内运行，例子包括快速排序（quicksort）、归并排序（mergesort）和堆排序（heapsort） | | O(n²) | 二次方 | 😩 | 10x the data take100x more time | 完成所需耗费的时间与 输入数据大小以`^2` 的关系增长。当您有一个遍历所有元素的循环时，该循环的每次迭代也会遍历每个元素。这是一个嵌套循环！ | | O(2^n) | 指数 | 😱 | —— | 完成所需耗费的时间与输入大小的关系以 `2^` 增长。它比 `n^2` 慢多了，所以不要把它们混淆了！如递归斐波那契算法 | ## O(1) O（1）称为恒定时间。具有常数的算法不会随输入大小缩放，无论输入多大，它们都是恒定的。这里有几个恒定的函数： ``` function value_at(arr, posn){ value = arr[posn] console.log("value:",value); } ``` 无论怎么样，这段函数不受任何参数影响，代码走一遍就完事，这种的代码用 T (n) = O (1) 表示。 我们经常看到 O(1) 是常数，但是1用任何数都可以用，它仍然是常数。我们会把数字改成1，因为这与需要多少步无关。只是记录它需要多少步完成。 ## O(log n) O（log n）称为对数时间。为此，假设我们有一个包含**有序元素的数组**，并且我们试图找到一个元素。那如何找到它？ 1. 遍历所有元素，直到找到它。可行，但要花一点时间取决于元素。在 1 到 100 的元素数组中找到 1 是可以的，但是找到 65 则需要一段时间。 2. 二分查找|对分查找，通过重复地将数据集减半，直到找到目标值，来缩小查找范围。 二分查找具有对数时间。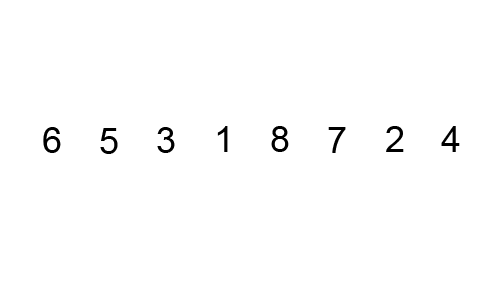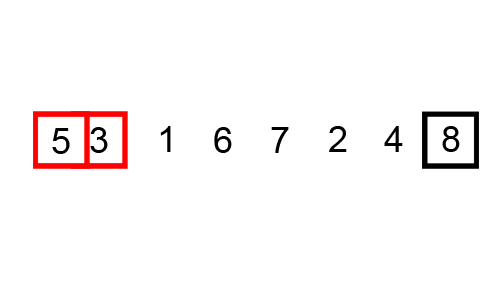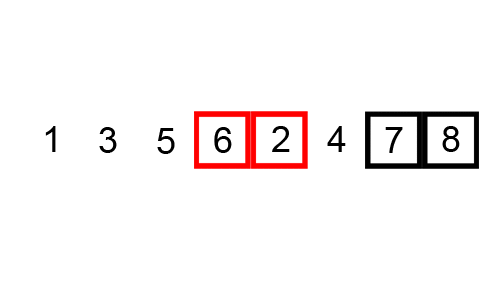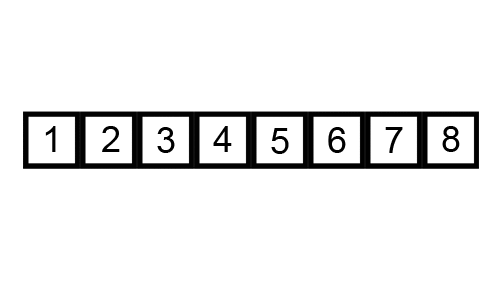 这是[二分查找](https://brilliant.org/wiki/binary-search/)图：  二分查找代码： ``` function binary_search(arr, item) { let first = 0; let last = arr.length - 1; while (first <= last) { // 相等情况 const midpoint = parseInt((first + last) / 2); // 下标取整 if (arr[midpoint] == item) { return true; // 找到直接返回 true } if (item < arr[midpoint]) { last = midpoint - 1; } else { first = midpoint + 1; } } return false; } ``` ## O(n) O(n) 被描述为线性时间。这意味着对于给定的算法，时间将随着数据集大小的增加而增加。让我们以一个数组为例，我们需要对它的项求和。大概是这样的： ``` function sum_add(num_array) { const n = num_array.length; for (var i = 0; i < n; i++) { sum += i; } console.log("sum",sum); } ``` `sum_add` 简单地接受一个数组，循环遍历每个元素，然后添加所有内容，然后输出 `sum`。 一个包含10个条目的数组肯定比一个包含 100 万个条目的数组要快。通俗易懂，这段代码的执行时间完全由 N 来控制，所以说 `T (n) = O (n)`。许多遍历数组的代码是 `O(n)`。 ## O(n log n) O(n log n) 是 linearithmic 时间。一个例子是归并排序。如果我们有一个未排序的数组，我们希望它是按升序排列的。归并排序将递归地将这个大数组分解成2个或更少元素的小数组，然后对这两个元素排序，然后将它们合并，使元素按升序组织。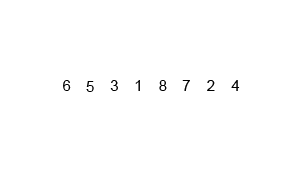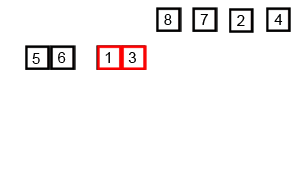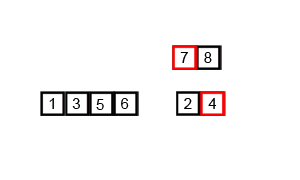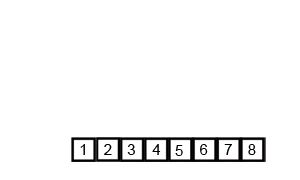 这图展示了归并排序的过程：  ``` def merge_sort(arr) return arr unless arr.size > 1 mid = arr.size/2 a, b, sorted = merge_sort(arr[0...mid]), merge_sort(arr[mid..-1]), [] sorted << (a[0] < b[0] ? a.shift : b.shift) while [a,b].none?(&:empty?) sorted + a + b end ``` ## O(n²) O(n²) 是二次的，这意味着 10倍的数据将花费 100倍的时间。我们刚刚看到 O(n) 被用在 for 循环中，这意味着你有另一个嵌套的 for 循环。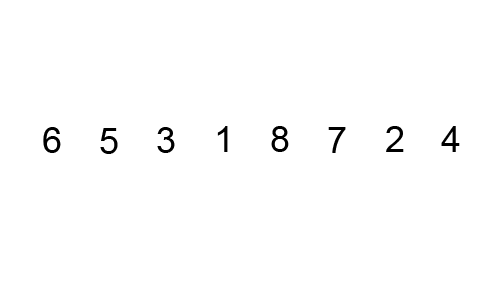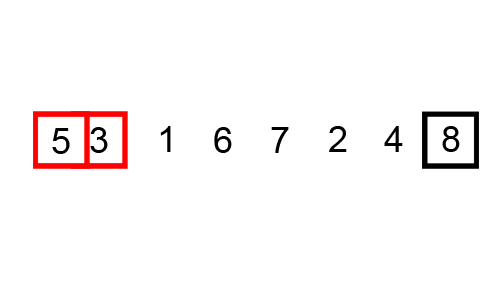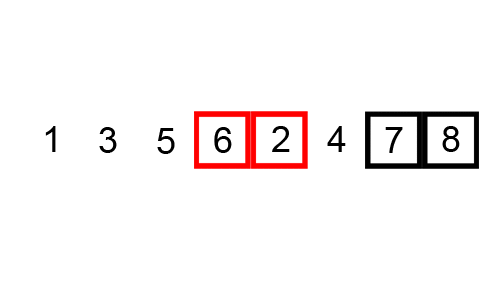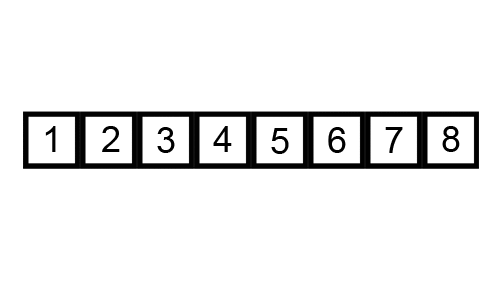 一个很好的例子是[冒泡排序](https://brilliant.org/wiki/bubble-sort)，这图来展示冒泡排序：  ``` def bubble_sort(arr) n=arr.length for i in 0...n-1 for j in 0...n-i-1 if arr[j]>arr[j+1] temp=arr[j] arr[j]=arr[j+1] arr[j+1]=temp end end end return arr end ``` 嵌套循环： ~~~ function go(i) { var sum = 0; for (var j = 0; j < i; j++) { sum += i; } return sum; } function main(n) { var res = 0; for (var i = 0; i < n; i++) { res = res + go(i); // 这里是重点 } } ~~~ 在上边的代码种第二段代码里边调用了第一段代码，所以说在这个代码里边是 ``` go:(1+n) ``` 在 `main` 函数里边的时候是`(1+n*go)=(1+n+n*n)` 所以最后的时间复杂度是 `T (n) = O (n²)` 这也意味着在一个`for`循环中嵌套的次数越多，对 n 的幂就越大，一个嵌套了2 个 for 循环的 `for` 循环会给出(3个 for 循环)`O(n³)`， 3个嵌套的`for`循环会给出 `O(n⁴)`，等等！所以在嵌套 for 循环时要非常小心！ ## O(2^n) 这是指数函数，也是最慢的。指数时间的一个例子是找到一个集合的所有子集。 让我们假设我们有一个叫做 `subsets` 的函数，该函数采用一个数组作为参数，并返回所有可能的子集。目的是采用数组并创建不同的值集。 ``` def subset(a) arr = [] for i in 0..(a.length) do arr = arr + a.combination(i).to_a end arr end ``` ``` >>> subsets(['']) [''] # 1 >>> subsets(['a']) ['', 'a'] # 2 >>> subsets(['a', 'b']) ['', 'a', 'ab', 'b'] # 4 >>> subsets('a', 'b', 'c']) ['', 'a', 'b', 'c', 'ab', 'ac', 'bc', 'abc'] # 8 ``` 当数组(a)有2个元素时我们有4个元素的输出，这是 2²，当输入有3个元素时我们有8个元素的输出，2³。 输出呈指数增长。 ## 如何计算时间复杂度 我们将利用现有的知识来尝试找出每种情况的复杂性。记住，我们需要考虑最坏的情况。 ### 例1 举个例子 ~~~ function go(n) { var item = 0; // 这里执行了一次 for (var i = 0; i < n; i++) { //这里执行了N次 for (var j = 0; j < n; j++) { //这里执行了n*n次 item = item + i + j; //这里执行了n*n次 } } return item; //这里执行了一次 } ~~~ 所以说上边这段代码是**1+n+n\*n\*2+1=2+n+2n²** 也就是说 `T (n) = O (f (2+n+2n²))` 然后之前说了时间复杂度看的是一个代码执行的时间的趋势， 所以说在 N，也就是规模比较大的时候，那些常量是起不到决定性的作用的，所以这个时候我们忽略这些常量，这里的例子是一个单段的代码，这里只看最大量级的循环就可以了 所以最后的这个代码的时间复杂度是 `T (n) = O (n²)` ### 例2 我们有一个电影列表，每部电影都有一个评级。我们希望找到一部电影，然后使用该电影的评级来查找其他具有类似评级的电影。 我们可以使用二分查找`O(log n)`来找到电影因为这样更快，但这只是我们需要找到其他电影的一部分，我们还需要再次遍历这个列表会用到我们的序列函数 `O(n)`，总的来说：`O(n log n)`还不错。 我们现在可以在更高的层次上尝试找出我们的算法，现在我们知道了： * halving（对分）=> O(log n) * for loops（for 循环）=> O(n) * nested for loops（嵌套的 for 循环） => O(n²) … 为了更好地理解如何计算时间复杂度，这里有一些链接： \- With [discrete maths](https://skerritt.blog/big-o/#-how-to-calculate-big-o-notation-of-a-function-discrete-maths-) \- Some [exercises with solutions](https://github.com/sf-wdi-31/algorithm-complexity-and-big-o) # 空间复杂度 空间复杂度是一个算法 / 程序使用的内存空间的总量的趋势，包括用于执行的输入值的空间。 空间复杂性常常与辅助空间混淆（*auxiliary space*）。辅助空间是算法使用的临时或额外空间。 简而言之： ``` 空间复杂度 = 辅助空间 + 输入值使用的空间 ``` 空间复杂度使用与时间复杂度相同的符号法： O(n)、O(1) 等等。 让我们看看这个使用ruby的简单函数，并尝试找出它的空间复杂度 ``` def sum array = [1,2,3] sum = 0 array.each {|i| sum = sum + i} puts sum end sum ``` 在 sum 函数中，我们有一个由 3 个元素组成的数组，我们循环遍历这些元素，并在执行过程中将它们相加，完成后，我们打印出这些元素的和。 现在要算出它的空间复杂度，在我们深入之前知道整数的空间复杂度是 O(1) 是很重要的。因此，看看这个函数，我们有一个数组和两个整数（sum, i）。 一个数组可以有任意数量的元素，n。数组占用的空间是 `4*n`个字节。假设每个整数占用 4 个字节，我们的整数占用 8 个字节。总空间是 `4n + 8`。消去常数，得到4n。函数的空间复杂度是 O(n) 线性复杂度。 # 小结 这里是一个[大O备忘单](https://www.bigocheatsheet.com/)，显示了不同数据结构和数组排序算法的不同空间和时间复杂性。 # 参考 [https://github.com/trekhleb/javascript-algorithms](https://github.com/trekhleb/javascript-algorithms) [JavaScript 算法](https://juejin.im/post/5c9a1d58e51d4559bb5c6694) [JavaScript 算法之复杂度分析](https://juejin.im/post/5c2a1d9d6fb9a04a0f654581#heading-8) [从 js 讲解时间复杂度和空间复杂度](https://www.ucloud.cn/yun/106364.html) [Data Structures with JavaScript](https://www.codeproject.com/Articles/669131/Data-Structures-with-JavaScript) [JavaScript 算法与数据结构](https://github.com/trekhleb/javascript-algorithms/blob/master/README.zh-CN.md) [Big O Notation — Time & Space Complexity in Ruby!](https://medium.com/@mendozabridget777/big-o-notation-time-space-complexity-9bc31952052c) [Bigocheatsheet](http://bigocheatsheet.com/) 介绍了计算机科学中常用算法的时空Big-O复杂性