**本节内容：** [TOC] ## 0.1 课前提问 1. 选哪些特征属性参与决策树建模？哪些属性排在决策树的顶部？哪些属性排在底部？ 2. 对属性的值该进行什么样的判断？ 3. 样本属性值缺失怎么办？ 4. 如果输出不是分类而是数值是否可用？ 5. 对决策没有用或者没有多大帮助的属性怎么办？ 6. 什么情况下使用决策树算法？ ## 0.2 引言 决策树学习采用的是自顶向下的递归方法，其基本思想是以信息熵为度量构造一颗熵值下降最快的树，到叶子节点处，熵值为0。其具有可读性、分类速度快的优点，是一种有监督学习。最早提及决策树思想的是Quinlan在1986年提出的ID3算法和1993年提出的C4.5算法，以及Breiman等人在1984年提出的CART算法。本篇文章主要介绍决策树的基本概念，以及上面这3种常见决策树算法（ID3、C4.5、CART）原理及其代码实现。 ## 1. 决策树算法简介 > 决策树（decision tree）是一类很常见很经典的机器学习算法，既可以作为分类算法也可以作为回归算法。同时也适合许多集成算法，如 RandomForest, XGBoost。 ### 1.1 决策树是什么？ 决策树是一类常见的机器学习方法，可以帮助我们解决<strong style="color:red;">分类与回归</strong>两类问题。 > 分类和回归树（简称 CART）是 Leo Breiman 引入的术语，指用来解决分类或回归预测建模问题的决策树算法。它常使用 scikit 生成并实现决策树： sklearn.tree.DecisionTreeClassifier 和 sklearn.tree.DecisionTreeRegressor 分别构建分类和回归树。 * 模型可解释性强，模型符合人类思维方式，是经典的树型结构。 * 决策树呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。 * <strong style="color:red;">决策树内部结点表示一个特征或属性，叶子节点表示一个类别。</strong><br/> 学习时，利用训练数据，根据损失函数最小化的原则建立决策树模型； 预测时，对新的数据，利用决策模型进行分类。<br/> <strong style="color:green;">【敲黑板，划重点】</strong> * 决策树是一个多层if-else函数，对对象属性进行多层if-else判断，从而获取目标属性的类别。 * 由于只是用if-else对特征属性进行判断，所以一般特征属性为离散值； * <strong>即使为连续值也会先进行区间离散化，如可以采用二分法。</strong> <strong style="color:red;">决策树的分类</strong>：决策树可以分为两类，主要取决于它目标变量的类型。 * 离散性决策树：离散性决策树，其目标变量是离散的，如性别：男或女等； * 连续性决策树：连续性决策树，其目标变量是连续的，如工资、价格、年龄等； ### 1.2 决策树特点 优点： * 具有可读性，如果给定一个模型，那么过呢据所产生的决策树很容易推理出相应的逻辑表达。 * 分类速度快，能在相对短的时间内能够对大型数据源做出可行且效果良好的结果。 缺点： * 对未知的测试数据未必有好的分类、泛化能力，即可能发生过拟合现象，此时可采用剪枝或随机森林。 适用数据类型： * <strong style="color:red;">数值型和标称型</strong> ## 2. 决策树算法 ### 2.1 决策树算法有哪些实现？ 关于决策树的主要思想，包括3项主要研究成果： | 算法 | 支持模型 | 树结构 | 特征选择 | 连续值处理 | 缺失值处理 | 剪枝 | 提出时间 | | --- | --- | --- | --- | --- | --- | --- | --- | | ID3 | 分类 | 多叉树 | 信息增益 | 不支持 | 不支持 | 不支持 | Quinlan于1986年提出 | | C4.5 | 分类 | 多叉树 | 信息增益比 | 支持 | 支持 | 支持 | Quinlan于1993年提出 | | CART | 分类、回归 | 二叉树 | 基尼系数、均方差 | 支持 | 支持 | 支持 | Breiman等人于1984年提出 | <br/> 递归学习过程：  ### 2.2 决策树的一般流程 （1）收集数据：可以使用任何方法； （2）准备数据：树构造算法只适用于标称型数据，因此数值型数据必须离散化； （3）分析数据：可以使用任何方法，构造树完成之后，我们应该检查图形是否符合预期； （4）训练算法：构造树的数据结构； （5）测试算法：使用经验树计算错误率； （6）使用算法：此步骤可以适用于任何监督学习算法，而使用决策树可以更好地理解数据的内在含义。 #### 2.2.1 决策树的构造过程 决策树的构造过程一般分为3个部分，分别是：<strong style="color:green;">特征选择、决策树的生成、决策树的剪枝。</strong><br/> （1）特征选择 特征选择表示从众多的特征中选择一个特征作为当前节点分裂的标准，如何选择特征有不同的量化评估方法，从而衍生出不同的决策树，如ID3（通过信息增益选择特征）、C4.5（通过信息增益比选择特征）、CART（通过Gini指数选择特征）等。 <strong style="color:red;">目的（准则）</strong>：使用某特征对数据集划分之后，各数据子集的纯度要比划分前的数据集的纯度高（也就是不确定性要比划分前数据集的不确定性低）<br/> （2）决策树的生成 根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止生长。这个过程实际上就是使用满足划分准则的特征不断的将数据集划分成纯度更高，不确定性更小的子集的过程。对于当前数据集的每一次划分，都希望根据某个特征划分之后的各个子集的纯度更高，不确定性更小。<br/> （3）决策树的剪枝 决策树容易过拟合，一般需要剪枝来缩小树结构规模、缓解过拟合。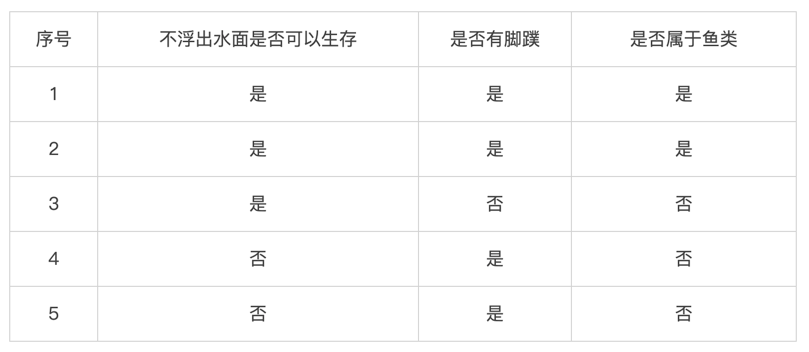<br/> 构成决策树的原始数据：   <br/> <br/> 接下来算法均采用相同数据集进行考量： <br/> ### 2.3 ID3（Iterative Dichotomiser 3）算法原理 ID3算法的核心是在决策树各个节点上应用信息增益准则选择特征递归地构建决策树。 #### 2.3.1 信息增益 **（1） 熵** 在信息论中，熵（entropy）是随机变量不确定性的度量，也就是熵越大，则随机变量的不确定性越大。设X是一个取有限个值得离散随机变量，其概率分布为：  则随机变量X的熵定义为：  **（2） 条件熵** 设有随机变量（X, Y），其联合概率分布为：  条件熵H(Y|X)表示在已知随机变量X的条件下，随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵H(Y|X)，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：  当熵和条件熵中的概率由数据估计得到时（如极大似然估计），所对应的熵与条件熵分别称为经验熵和经验条件熵。 **（3）信息增益** **定义：** 信息增益表示由于得知特征A的信息后而使得数据集D的分类不确定性减少的程度，定义为： Gain(D,A) = H(D) – H(D|A) 即集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(H|A)之差。 **理解：** 选择划分后信息增益大的作为划分特征，说明使用该特征后划分得到的子集纯度越高，即不确定性越小。因此我们总是选择当前使得信息增益最大的特征来划分数据集。 **缺点：** 信息增益偏向取值较多的特征（原因：当特征的取值较多时，根据此特征划分更容易得到纯度更高的子集，因此划分后的熵更低，即不确定性更低，因此信息增益更大）<br/> **计算香农熵的代码实现：** ~~~ def calc_shannon_ent(data_set): """ 计算信息熵 :param data_set: 如： [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] :return: """ num = len(data_set) # n rows # 为所有的分类类目创建字典 label_counts = {} for feat_vec in data_set: current_label = feat_vec[-1] # 取得最后一列数据 if current_label not in label_counts.keys(): label_counts[current_label] = 0 label_counts[current_label] += 1 # 计算香农熵 shannon_ent = 0.0 for key in label_counts: prob = float(label_counts[key]) / num shannon_ent = shannon_ent - prob * log(prob, 2) return shannon_ent ~~~ * 第一个for循环：为所有可能分类创建字典 * 第二个for循环：以2为底求对数 创建数据集代码： ~~~ def create_data_set(): """ 创建样本数据 :return: """ data_set = [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] labels = ['no surfacing', 'flippers'] return data_set, labels ~~~ 我们分析下熵和混合的数据多少的关系，通过再数据集中添加更多的分类，观察熵是如何变化的：  > 结论：熵越高，则混合的数据也越多。 #### 2.3.2 ID3算法 ~~~ 输入：训练数据集D，特征集A，阈值ε 输出：决策树T Step1：若D中所有实例属于同一类，则T为单结点树，并将类作为该节点的类标记，返回T； Step2：若A=Ø，则T为单结点树，并将D中实例数最大的类作为该节点的类标记，返回T； Step3：否则，计算A中每个特征对D的信息增益，选择信息增益最大的特征； Step4：如果的信息增益小于阈值ε，则T为单节点树，并将D中实例数最大的类作为该节点的类标记，返回T Step5：否则，对的每一种可能值，依将D分割为若干非空子集，将中实例数最大的类作为标记，构建子结点，由结点及其子树构成树T，返回T； Step6：对第i个子节点，以为训练集，以为特征集合，递归调用Step1~step5，得到子树，返回； ~~~ #### 2.3.3 代码实现 ~~~ # -*- coding: utf-8 -*- from math import log import operator import tree_plotter def create_data_set(): """ 创建样本数据 :return: """ data_set = [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] labels = ['no surfacing', 'flippers'] return data_set, labels def calc_shannon_ent(data_set): """ 计算信息熵 :param data_set: 如： [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] :return: """ num = len(data_set) # n rows # 为所有的分类类目创建字典 label_counts = {} for feat_vec in data_set: current_label = feat_vec[-1] # 取得最后一列数据 if current_label not in label_counts.keys(): label_counts[current_label] = 0 label_counts[current_label] += 1 # 计算香浓熵 shannon_ent = 0.0 for key in label_counts: prob = float(label_counts[key]) / num shannon_ent = shannon_ent - prob * log(prob, 2) return shannon_ent def split_data_set(data_set, axis, value): """ 返回特征值等于value的子数据集，切该数据集不包含列（特征）axis :param data_set: 待划分的数据集 :param axis: 特征索引 :param value: 分类值 :return: """ ret_data_set = [] for feat_vec in data_set: if feat_vec[axis] == value: reduce_feat_vec = feat_vec[:axis] reduce_feat_vec.extend(feat_vec[axis + 1:]) ret_data_set.append(reduce_feat_vec) return ret_data_set def choose_best_feature_to_split(data_set): """ 按照最大信息增益划分数据 :param data_set: 样本数据，如： [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] :return: """ num_feature = len(data_set[0]) - 1 # 特征个数，如：不浮出水面是否可以生存 和是否有脚蹼 base_entropy = calc_shannon_ent(data_set) # 经验熵H(D) best_info_gain = 0 best_feature_idx = -1 for feature_idx in range(num_feature): feature_val_list = [number[feature_idx] for number in data_set] # 得到某个特征下所有值（某列） unique_feature_val_list = set(feature_val_list) # 获取无重复的属性特征值 new_entropy = 0 for feature_val in unique_feature_val_list: sub_data_set = split_data_set(data_set, feature_idx, feature_val) prob = len(sub_data_set) / float(len(data_set)) # 即p(t) new_entropy += prob * calc_shannon_ent(sub_data_set) #对各子集香农熵求和 info_gain = base_entropy - new_entropy # 计算信息增益，g(D,A)=H(D)-H(D|A) # 最大信息增益 if info_gain > best_info_gain: best_info_gain = info_gain best_feature_idx = feature_idx return best_feature_idx def majority_cnt(class_list): """ 统计每个类别出现的次数，并按大到小排序，返回出现次数最大的类别标签 :param class_list: 类数组 :return: """ class_count = {} for vote in class_list: if vote not in class_count.keys(): class_count[vote] = 0 class_count[vote] += 1 sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reversed=True) print sorted_class_count[0][0] return sorted_class_count[0][0] def create_tree(data_set, labels): """ 构建决策树 :param data_set: 数据集合，如： [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] :param labels: 标签数组，如：['no surfacing', 'flippers'] :return: """ class_list = [sample[-1] for sample in data_set] # ['yes', 'yes', 'no', 'no', 'no'] # 类别相同，停止划分 if class_list.count(class_list[-1]) == len(class_list): return class_list[-1] # 长度为1，返回出现次数最多的类别 if len(class_list[0]) == 1: return majority_cnt((class_list)) # 按照信息增益最高选取分类特征属性 best_feature_idx = choose_best_feature_to_split(data_set) # 返回分类的特征的数组索引 best_feat_label = labels[best_feature_idx] # 该特征的label my_tree = {best_feat_label: {}} # 构建树的字典 del (labels[best_feature_idx]) # 从labels的list中删除该label，相当于待划分的子标签集 feature_values = [example[best_feature_idx] for example in data_set] unique_feature_values = set(feature_values) for feature_value in unique_feature_values: sub_labels = labels[:] # 子集合 # 构建数据的子集合，并进行递归 sub_data_set = split_data_set(data_set, best_feature_idx, feature_value) # 待划分的子数据集 my_tree[best_feat_label][feature_value] = create_tree(sub_data_set, sub_labels) return my_tree def classify(input_tree, feat_labels, test_vec): """ 决策树分类 :param input_tree: 决策树 :param feat_labels: 特征标签 :param test_vec: 测试的数据 :return: """ first_str = list(input_tree.keys())[0] # 获取树的第一特征属性 second_dict = input_tree[first_str] # 树的分子，子集合Dict feat_index = feat_labels.index(first_str) # 获取决策树第一层在feat_labels中的位置 for key in second_dict.keys(): if test_vec[feat_index] == key: if type(second_dict[key]).__name__ == 'dict': class_label = classify(second_dict[key], feat_labels, test_vec) else: class_label = second_dict[key] return class_label data_set, labels = create_data_set() decision_tree = create_tree(data_set, labels) print "决策树：", decision_tree data_set, labels = create_data_set() print "（1）不浮出水面可以生存，无脚蹼：", classify(decision_tree, labels, [1, 0]) print "（2）不浮出水面可以生存，有脚蹼：", classify(decision_tree, labels, [1, 1]) print "（3）不浮出水面可以不能生存，无脚蹼：", classify(decision_tree, labels, [0, 0]) tree_plotter.create_plot(decision_tree) ~~~ 画图程序 tree_plotter.py： ~~~ import matplotlib.pyplot as plt decision_node = dict(boxstyle="sawtooth", fc="0.8") leaf_node = dict(boxstyle="round4", fc="0.8") arrow_args = dict(arrowstyle="<-") def plot_node(node_txt, center_pt, parent_pt, node_type): create_plot.ax1.annotate(node_txt, xy=parent_pt, xycoords='axes fraction', \ xytext=center_pt, textcoords='axes fraction', \ va="center", ha="center", bbox=node_type, arrowprops=arrow_args) def get_num_leafs(my_tree): num_leafs = 0 first_str = list(my_tree.keys())[0] second_dict = my_tree[first_str] for key in second_dict.keys(): if type(second_dict[key]).__name__ == 'dict': num_leafs += get_num_leafs(second_dict[key]) else: num_leafs += 1 return num_leafs def get_tree_depth(my_tree): max_depth = 0 first_str = list(my_tree.keys())[0] second_dict = my_tree[first_str] for key in second_dict.keys(): if type(second_dict[key]).__name__ == 'dict': thisDepth = get_tree_depth(second_dict[key]) + 1 else: thisDepth = 1 if thisDepth > max_depth: max_depth = thisDepth return max_depth def plot_mid_text(cntr_pt, parent_pt, txt_string): x_mid = (parent_pt[0] - cntr_pt[0]) / 2.0 + cntr_pt[0] y_mid = (parent_pt[1] - cntr_pt[1]) / 2.0 + cntr_pt[1] create_plot.ax1.text(x_mid, y_mid, txt_string) def plot_tree(my_tree, parent_pt, node_txt): num_leafs = get_num_leafs(my_tree) depth = get_tree_depth(my_tree) first_str = list(my_tree.keys())[0] cntr_pt = (plot_tree.x_off + (1.0 + float(num_leafs)) / 2.0 / plot_tree.total_w, plot_tree.y_off) plot_mid_text(cntr_pt, parent_pt, node_txt) plot_node(first_str, cntr_pt, parent_pt, decision_node) second_dict = my_tree[first_str] plot_tree.y_off = plot_tree.y_off - 1.0 / plot_tree.total_d for key in second_dict.keys(): if type(second_dict[key]).__name__ == 'dict': plot_tree(second_dict[key], cntr_pt, str(key)) else: plot_tree.x_off = plot_tree.x_off + 1.0 / plot_tree.total_w plot_node(second_dict[key], (plot_tree.x_off, plot_tree.y_off), cntr_pt, leaf_node) plot_mid_text((plot_tree.x_off, plot_tree.y_off), cntr_pt, str(key)) plot_tree.y_off = plot_tree.y_off + 1.0 / plot_tree.total_d def create_plot(in_tree): fig = plt.figure(1, facecolor='white') fig.clf() axprops = dict(xticks=[], yticks=[]) create_plot.ax1 = plt.subplot(111, frameon=False, **axprops) plot_tree.total_w = float(get_num_leafs(in_tree)) plot_tree.total_d = float(get_tree_depth(in_tree)) plot_tree.x_off = -0.5 / plot_tree.total_w plot_tree.y_off = 1.0 plot_tree(in_tree, (0.5, 1.0), '') plt.show() ~~~ 运行结果：   ### 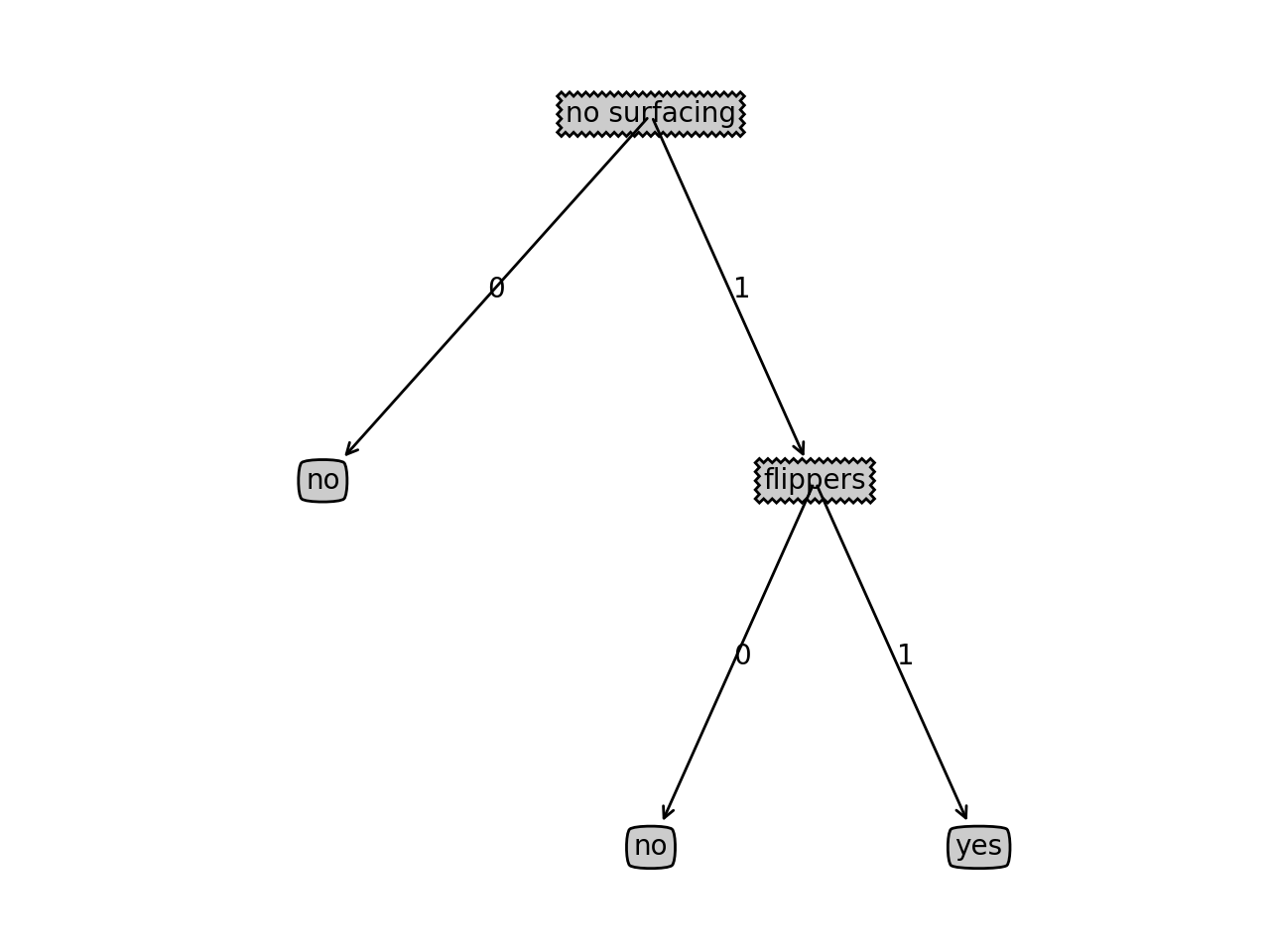2.4 C4.5算法原理 C4.5算法与ID3算法很相似，C4.5算法是对ID3算法做了改进，在生成决策树过程中采用信息增益比来选择特征。 #### 2.4.1信息增益比 我们知道信息增益会偏向取值较多的特征，使用信息增益比可以对这一问题进行校正。 **定义**：特征A对训练数据集D的信息增益比GainRatio(D,A)定义为其信息增益Gain(D,A)与训练数据集D的经验熵H(D)之比：  #### 2.4.2 C4.5算法 C4.5算法过程跟ID3算法一样，只是选择特征的方法由信息增益改成信息增益比。 具体过程，同2.3.2 #### 2.4.3 代码实现 我们还是采用2.1.3中的实例，C4.5算法跟ID3算法，不同的地方只是特征选择方法，即调整特征选择方法代码即可： ~~~ def choose_best_feature_to_split(data_set): """ 按照最大信息增益比划分数据 :param data_set: 样本数据，如： [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] :return: """ num_feature = len(data_set[0]) - 1 # 特征个数，如：不浮出水面是否可以生存 和是否有脚蹼 base_entropy = calc_shannon_ent(data_set) # 经验熵H(D) best_info_gain_ratio = 0.0 best_feature_idx = -1 for feature_idx in range(num_feature): # 得到某个特征下所有值（某列） feature_val_list = [number[feature_idx] for number in data_set] # 获取无重复的属性特征值 unique_feature_val_list = set(feature_val_list) new_entropy = 0 split_info = 0.0 for value in unique_feature_val_list: sub_data_set = split_data_set(data_set, feature_idx, value) # 即p(t) prob = len(sub_data_set) / float(len(data_set)) # 对各子集香农熵求和 new_entropy += prob * calc_shannon_ent(sub_data_set) split_info += -prob * log(prob, 2) # 计算信息增益，g(D,A)=H(D)-H(D|A) info_gain = base_entropy - new_entropy if split_info == 0: # fix the overflow bug continue info_gain_ratio = info_gain / split_info # 最大信息增益比 if info_gain_ratio > best_info_gain_ratio: best_info_gain_ratio = info_gain_ratio best_feature_idx = feature_idx return best_feature_idx ~~~ ### 2.5 CART算法原理 > CART树里面对C4.5中存在的问题进行了改进。CART假设决策树是二叉树，并且可以分类也可以回归，而且用基尼指数代替了熵模型进行特征选择，也提供了优化的剪枝策略。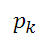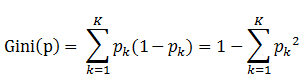 #### 2.5.1 Gini指数 分类问题中，假设有K个类，样本点属于第k类的概率为，则概率分布的基尼指数定义为：  备注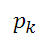：表示选中的样本属于k类别的概率，则这个样本被分错的概率为 对于给定的样本集合D，其基尼指数为：  备注：这里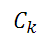是D中属于第k类的样本自己，K是类的个数。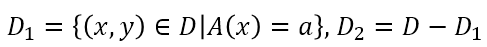 如果样本集合D根据特征A是否取某一可能值a被分割成D1和D2两部分，即：  则在特征A的条件下，集合D的基尼指数定义为：  基尼指数Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。基尼指数值越大，样本集合的不确定性也就越大，这一点跟熵相似。 <strong style="color:green;">[看例子解读]</strong> 如下，是一个包含30个学生的样本，其包含三种特征，分别是：性别（男/女）、班级（IX/X）和高度（5到6ft）。其中30个学生里面有15个学生喜欢在闲暇时间玩板球。那么要如何选择第一个要划分的特征呢，我们通过上面的公式来进行计算。  如下，可以Gini(D,Gender)最小，所以选择性别作为最优特征。  #### 2.5.2 CART算法 ~~~ 输入：训练数据集D，停止计算的条件 输出：CART决策树 根据训练数据集，从根结点开始，递归地对每个结点进行以下操作，构建二叉树： Step1：设结点的训练数据集为D，计算现有特征对该数据集的基尼指数。此时，对每一个特征A，对其可能取的每个值a，根据样本点A=a的测试为“是”或“否”将D分割为D1和D2两部分，利用上式Gini(D,A)来计算A=a时的基尼指数。 Step2：在所有可能的特征A以及他们所有可能的切分点a中，选择基尼指数最小的特征及其对应可能的切分点作为最有特征与最优切分点。依最优特征与最有切分点，从现结点生成两个子节点，将训练数据集依特征分配到两个子节点中去。 Step3：对两个子结点递归地调用Step1、Step2，直至满足条件。 Step4：生成CART决策树 算法停止计算的条件是节点中的样本个数小于预定阈值，或样本集的基尼指数小于预定阈值，或者没有更多特征。 ~~~ #### 2.5.4 代码实现 ~~~ # -*- coding: utf-8 -*- import numpy as np class Tree(object): def __init__(self, value=None, true_branch=None, false_branch=None, results=None, col=-1, summary=None, data=None): self.value = value self.true_branch = true_branch self.false_branch = false_branch self.results = results self.col = col self.summary = summary self.data = data def __str__(self): print(self.col, self.value) print(self.results) print(self.summary) return "" def split_datas(rows, value, column): """ 根据条件分离数据集 :param rows: :param value: :param column: :return: (list1, list2) """ list1 = [] list2 = [] if isinstance(value, int) or isinstance(value, float): for row in rows: if row[column] >= value: list1.append(row) else: list2.append(row) else: for row in rows: if row[column] == value: list1.append(row) else: list2.append(row) return list1, list2 def calculate_diff_count(data_set): """ 分类统计data_set中每个类别的数量 :param datas:如：[[5.1, 3.5, 1.4, 0.2, 'setosa'], [4.9, 3, 1.4, 0.2, 'setosa'],....] :return: 如：{'setosa': 50, 'versicolor': 50, 'virginica': 50} """ results = {} for data in data_set: # 数据的最后一列data[-1]是类别 if data[-1] not in results: results.setdefault(data[-1], 1) else: results[data[-1]] += 1 return results def gini(data_set): """ 计算gini的值，即Gini(p) :param data_set: 如：[[5.1, 3.5, 1.4, 0.2, 'setosa'], [4.9, 3, 1.4, 0.2, 'setosa'],....] :return: """ length = len(data_set) category_2_cnt = calculate_diff_count(data_set) sum = 0.0 for category in category_2_cnt: sum += pow(float(category_2_cnt[category]) / length, 2) return 1 - sum def build_decision_tree(data_set, evaluation_function=gini): """ 递归建立决策树，当gain=0时，停止回归 :param data_set: 如：[[5.1, 3.5, 1.4, 0.2, 'setosa'], [4.9, 3, 1.4, 0.2, 'setosa'],....] :param evaluation_function: :return: """ current_gain = evaluation_function(data_set) column_length = len(data_set[0]) rows_length = len(data_set) best_gain = 0.0 best_value = None best_set = None # choose the best gain for feature_idx in range(column_length - 1): feature_value_set = set(row[feature_idx] for row in data_set) for feature_value in feature_value_set: sub_data_set1, sub_data_set2 = split_datas(data_set, feature_value, feature_idx) p = float(len(sub_data_set1)) / rows_length # Gini(D,A)表示在特征A的条件下集合D的基尼指数，gini_d_a越小，样本集合不确定性越小 # 我们的目的是找到另gini_d_a最小的特征，及gain最大的特征 gini_d_a = p * evaluation_function(sub_data_set1) + (1 - p) * evaluation_function(sub_data_set2) gain = current_gain - gini_d_a if gain > best_gain: best_gain = gain best_value = (feature_idx, feature_value) best_set = (sub_data_set1, sub_data_set2) dc_y = {'impurity': '%.3f' % current_gain, 'sample': '%d' % rows_length} # stop or not stop if best_gain > 0: true_branch = build_decision_tree(best_set[0], evaluation_function) false_branch = build_decision_tree(best_set[1], evaluation_function) return Tree(col=best_value[0], value=best_value[1], true_branch=true_branch, false_branch=false_branch, summary=dc_y) else: return Tree(results=calculate_diff_count(data_set), summary=dc_y, data=data_set) def prune(tree, mini_gain, evaluation_function=gini): """ 裁剪 :param tree: :param mini_gain: :param evaluation_function: :return: """ if tree.true_branch.results == None: prune(tree.true_branch, mini_gain, evaluation_function) if tree.false_branch.results == None: prune(tree.false_branch, mini_gain, evaluation_function) if tree.true_branch.results != None and tree.false_branch.results != None: len1 = len(tree.true_branch.data) len2 = len(tree.false_branch.data) len3 = len(tree.true_branch.data + tree.false_branch.data) p = float(len1) / (len1 + len2) gain = evaluation_function(tree.true_branch.data + tree.false_branch.data) \ - p * evaluation_function(tree.true_branch.data)\ - (1 - p) * evaluation_function(tree.false_branch.data) if gain < mini_gain: # 当节点的gain小于给定的 mini Gain时则合并这两个节点 tree.data = tree.true_branch.data + tree.false_branch.data tree.results = calculate_diff_count(tree.data) tree.true_branch = None tree.false_branch = None def classify(data, tree): """ 分类 :param data: :param tree: :return: """ if tree.results != None: return tree.results else: branch = None v = data[tree.col] if isinstance(v, int) or isinstance(v, float): if v >= tree.value: branch = tree.true_branch else: branch = tree.false_branch else: if v == tree.value: branch = tree.true_branch else: branch = tree.false_branch return classify(data, branch) def load_csv(): def convert_types(s): s = s.strip() try: return float(s) if '.' in s else int(s) except ValueError: return s data = np.loadtxt("datas.csv", dtype="str", delimiter=",") data = data[1:, :] data_set = ([[convert_types(item) for item in row] for row in data]) return data_set ~~~ <br/> ## 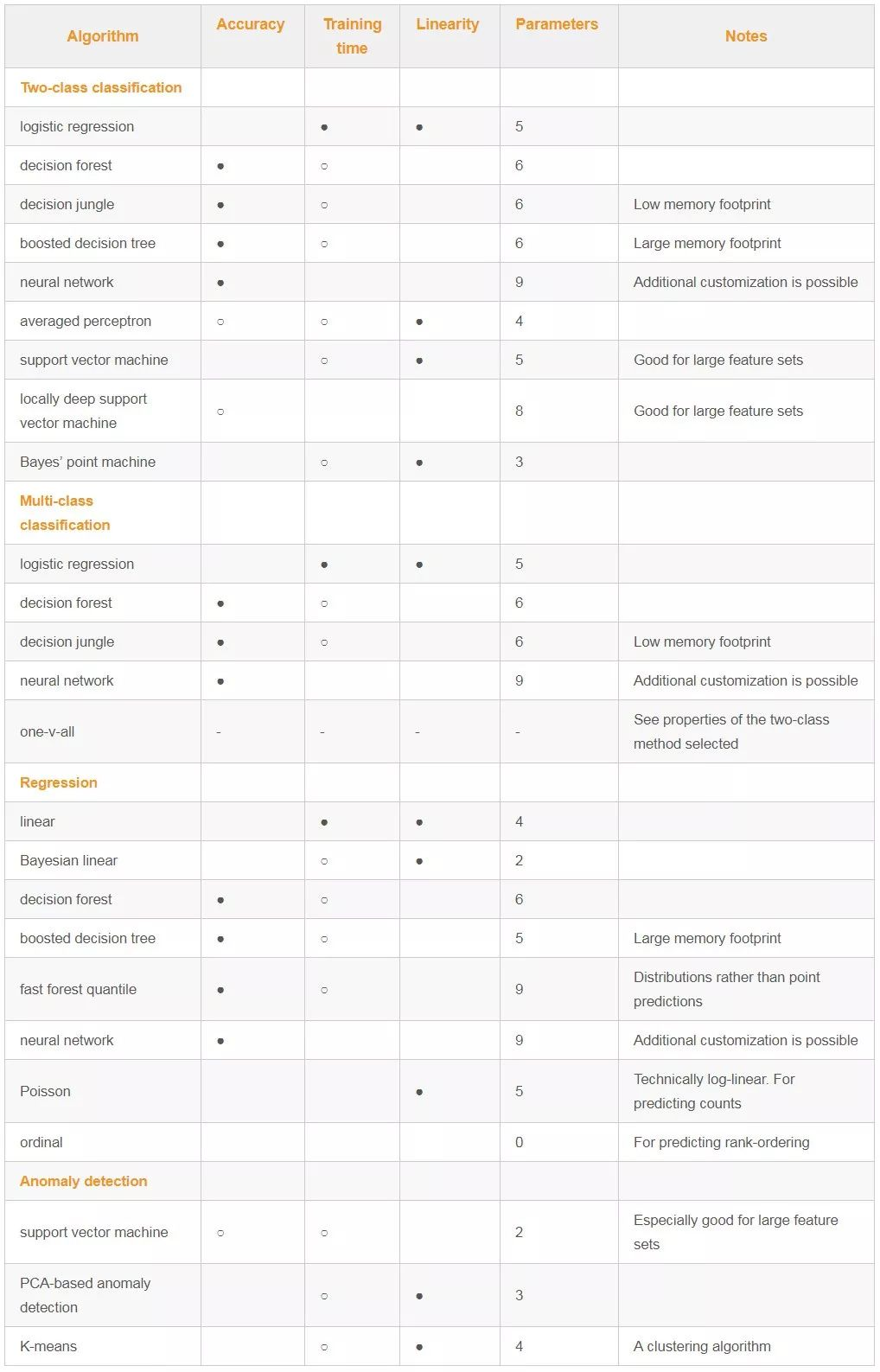2.6何时选择决策树算法？？？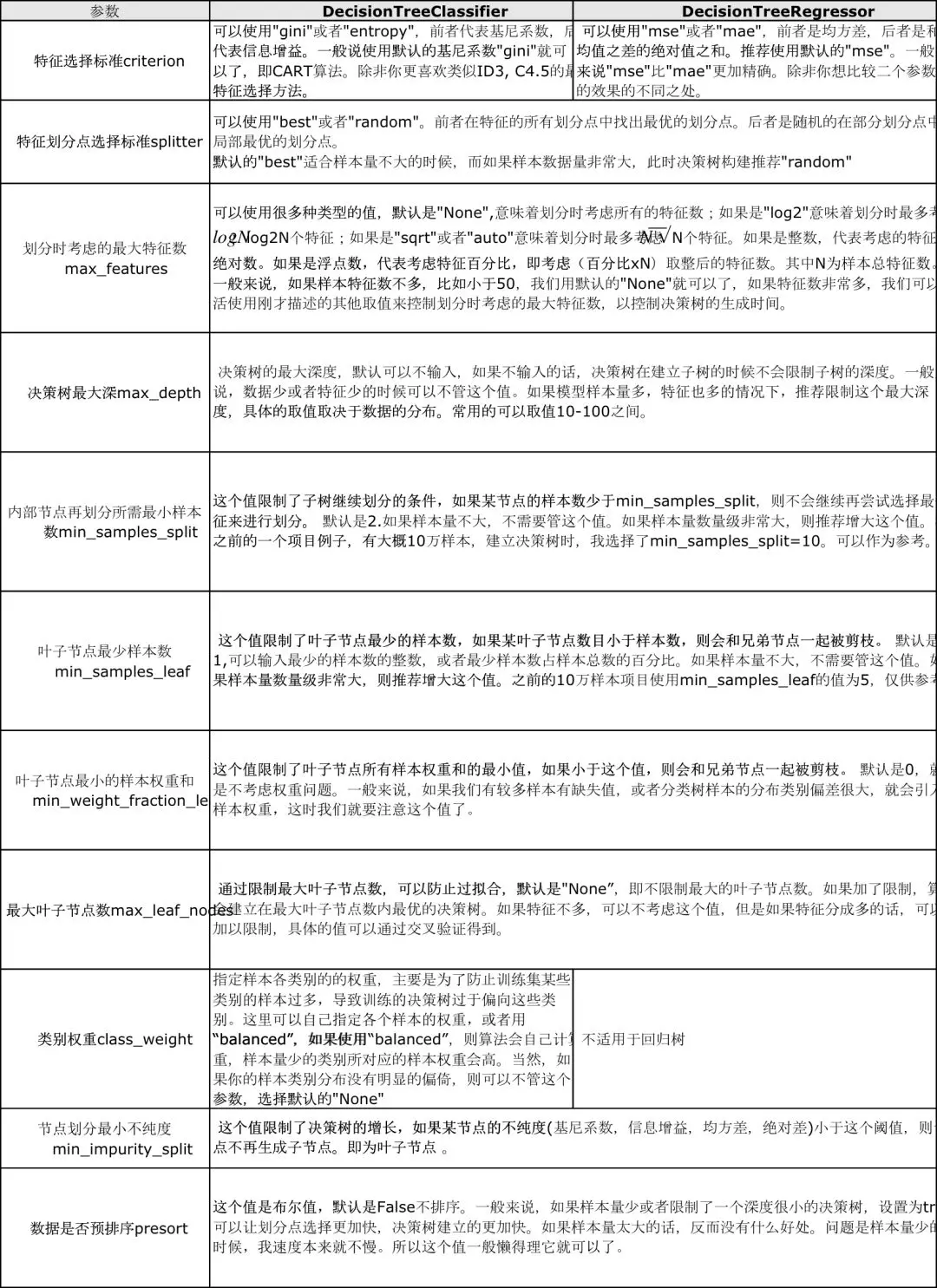 scikit-learn决策树使用指南：[https://scikit-learn.org/dev/modules/classes.html#module-sklearn.tree](https://scikit-learn.org/dev/modules/classes.html#module-sklearn.tree) 参数说明： <br/> 何时选择决策树算法？：  ## 3.总结 * ID3 * 局限性 * （1）不支持连续特征 * （2）采用信息增益大的特征优先建立决策树的节点。在相同条件下，取值比较多的特征比取值少的特征信息增益大。 * （3）不支持缺失值处理 * （4）没有应对过拟合的策略 * C4.5 * 局限性 * （1）剪枝的算法有非常多，C4.5的剪枝方法有优化的空间 * （2）C4.5生成的是多叉树，很多时候，在计算机中二叉树模型会比多叉树运算效率高。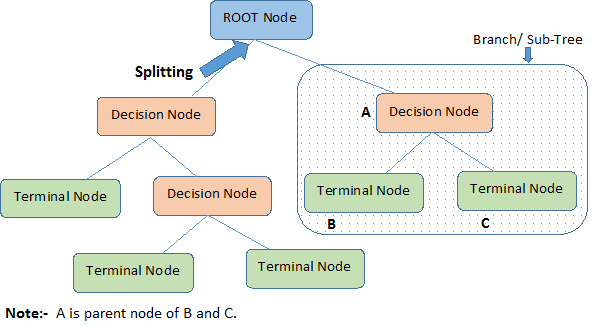如果采用二叉树，可以提高效率 * （3）C4.5只能用于分类 * （4）C4.5使用了熵模型，里面有大量的耗时的对数运算,如果是连续值还有大量的排序运算 * CART ## <strong>附录一：决策树相关的重要概念</strong> （1）根结点(Root Node)：它表示整个样本集合，并且该节点可以进一步划分成两个或多个子集。 （2）拆分(Splitting)：表示将一个结点拆分成多个子集的过程。 （3）决策结点(Decision Node)：当一个子结点进一步被拆分成多个子节点时，这个子节点就叫做决策结点。 （4）叶子结点(Leaf/Terminal Node)：无法再拆分的结点被称为叶子结点。 （5）剪枝(Pruning)：移除决策树中子结点的过程就叫做剪枝，跟拆分过程相反。 （6）分支/子树(Branch/Sub-Tree)：一棵决策树的一部分就叫做分支或子树。 （7）父结点和子结点(Paren and Child Node)：一个结点被拆分成多个子节点，这个结点就叫做父节点；其拆分后的子结点也叫做子结点。  ## <strong>附录二：参考资料</strong> * [决策树算法原理(上)](https://www.cnblogs.com/pinard/p/6050306.html) * [决策树算法的原理（接地气版）](https://my.oschina.net/u/3658210/blog/4526316) * [决策树例题](https://wenku.baidu.com/view/6eb1c1df1fd9ad51f01dc281e53a580217fc5011.html ) * [带你搞懂决策树算法原理](https://blog.csdn.net/akirameiao/article/details/79953980) * [python机器学习笔记：深入学习决策树算法原理](https://www.cnblogs.com/wj-1314/p/9428494.html) * [跟我一起学scikit-learn18：决策树算法](https://blog.csdn.net/u011436316/article/details/92141250) * [为什么在神经网络大放异彩的今天要学习决策树？](https://www.zhihu.com/question/54811425?sort=created) * [Python机器学习算法库scikit-learn学习之决策树实现方法详解](https://www.jb51.net/article/164614.htm) * 书籍推荐：[机器学习实战：基于Scikit-Learn和TensorFlow PDF下载](http://www.java1234.com/a/javabook/javabase/2018/1128/12462.html) ## <strong>附录三：算法比较图</strong>