# 附录 D、自动微分
> 译者:[@rickllyxu](https://github.com/rickllyxu)
这个附录解释了 TensorFlow 的自动微分功能是如何工作的,以及它与其他解决方案的对比。
假定你定义了函数 ,需要得到它的偏导数  和 ,以用于梯度下降或者其他优化算法。你的可选方案有手动微分法,符号微分法,数值微分法,前向自动微分,和反向自动微分。TensorFlow 实现的反向自动微分法。我们来看看每种方案。
## 手动微分法
第一个方法是拿起一直笔和一张纸,使用你的代数知识去手动的求偏导数。对于已定义的函数,求它的偏导并不太困难。你需要使用如下 5 条规则:
- 常数的导数为 0。
-  的导数为 , 为常数。
-  的导数是 
- 函数的和的导数,等于函数的导数的和
-  乘以函数,再求导,等于  乘以函数的导数
从上述这些规则,可得到公式 D-1。
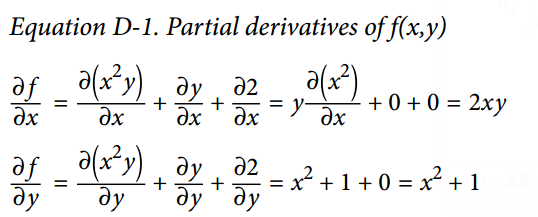
这个种方法应用于更复杂函数时将变得非常罗嗦,并且有可能出错。好消息是,像刚才我们做的求数学式子的偏导数可以被自动化,通过一个称为符号微分的过程。
## 符号微分
图 D-1 展示了符号微分是如何运行在相当简单的函数上的,。该函数的计算图如图的左边所示。通过符号微分,我们可得到图的右部分,它代表了 ,相似地也可得到关于`y`的导数。
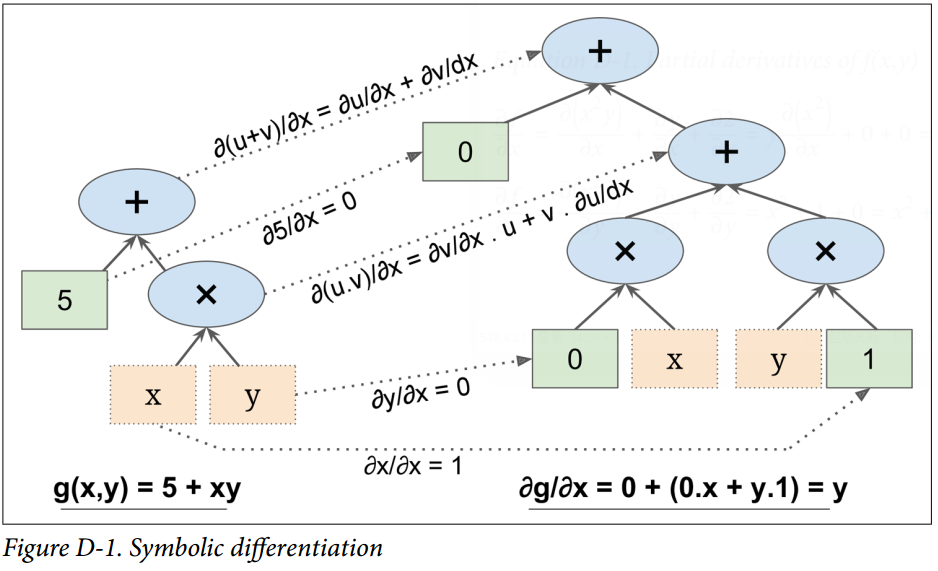
概算法先获得叶子节点的偏导数。常数 5 返回常数 0,因为常数的导数总是 0。变量`x`返回常数 1,变量`y`返回常数 0,因为 (如果我们找关于`y`的偏导数,那它将反过来)。
现在我们移动到计算图的相乘节点处,代数告诉我们,`u`和`v`相乘后的导数为 。因此我们可以构造有图中大的部分,代表`0 × x + y × 1`。
最后我们往上走到计算图的相加节点处,正如 5 条规则里提到的,和的导数等于导数的和。所以我们只需要创建一个相加节点,连接我们已经计算出来的部分。我们可以得到正确的偏导数,即:。
然而,这个过程可简化。对该图应用一些微不足道的剪枝步骤,可以去掉所有不必要的操作,然后我们可以得到一个小得多的只有一个节点的偏导计算图:。
在这个例子里,简化操作是相当简单的,但对更复杂的函数来说,符号微分会产生一个巨大的计算图,该图可能很难去简化,以导致次优的性能。更重要的是,符号微分不能处理由任意代码定义的函数,例如,如下已在第 9 章讨论过的函数:
```python
def my_func(a, b):
z = 0
for i in range(100):
z = a * np.cos(z + i) + z * np.sin(b - i)
return z
```
## 数值微分
从数值上说,最简单的方案是去计算导数的近似值。回忆`h(x)`在  的导数 ,是该函数在该点处的斜率,或者更准确如公式 D-2 所示。

因此如果我们想要计算  关于`x`,在  处的导数,我们可以简单计算  的值,将这个结果除以 ,且  去很小的值。这个过程正是如下的代码所要干的。
```python
def f(x, y):
return x**2*y + y + 2
def derivative(f, x, y, x_eps, y_eps):
return (f(x + x_eps, y + y_eps) - f(x, y)) / (x_eps + y_eps)
df_dx = derivative(f, 3, 4, 0.00001, 0)
df_dy = derivative(f, 3, 4, 0, 0.00001)
```
不幸的是,偏导的结果并不准确(并且可能在求解复杂函数时更糟糕)。上述正确答案分别是 24 和 10 ,但我们得到的是:
```python
>>> print(df_dx)
24.000039999805264
>>> print(df_dy)
10.000000000331966
```
注意到为了计算两个偏导数, 我们不得不调用`f()`至少三次(在上述代码里我们调用了四次,但可以优化)。如果存在 1000 个参数,我们将会调用`f()`至少 1001 次。当处理大的神经网络时,这样的操作很没有效率。
然而,数值微分实现起来如此简单,以至于它是检查其他方法正确性的优秀工具。例如,如果它的结果与您手动计算的导数不同,那么你的导数可能包含错误。
## 前向自动微分
前向自动微分既不是数值微分,也不是符号微分,但在某些方面,它是他们的爱情结晶。它依赖对偶数。对偶数是奇怪但迷人的,是  形式的数,这里`a`和`b`是实数, 是无穷小的数,满足 ,但 。你可以认为对偶数  类似于有着无穷个 0 的 42.0000⋯000024(但当然这是简化后的,仅仅给你对偶数什么的想法)。一个对偶数在内存中表示为一个浮点数对,例如, 表示为`(42.0, 24.0)`。
对偶数可相加、相乘、等等操作,正如公式 D-3 所示。
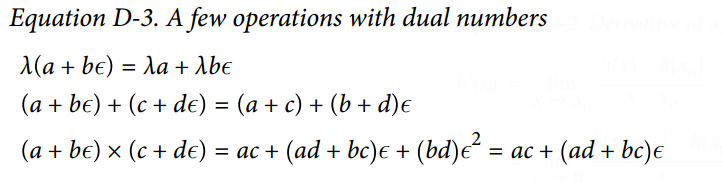
最重要的,可证明`h(a + bϵ) = h(a) + b × h'(a)ϵ`,所以计算一次`h(a + ϵ)`就得到了两个值`h(a)`和`h'(a)`。图 D-2 展示了前向自动微分如何计算  关于`x`,在  处的导数。我们所要做的一切只是计算 ;它将输出一个对偶数,其第一部分等于 ,第二部分等于 。
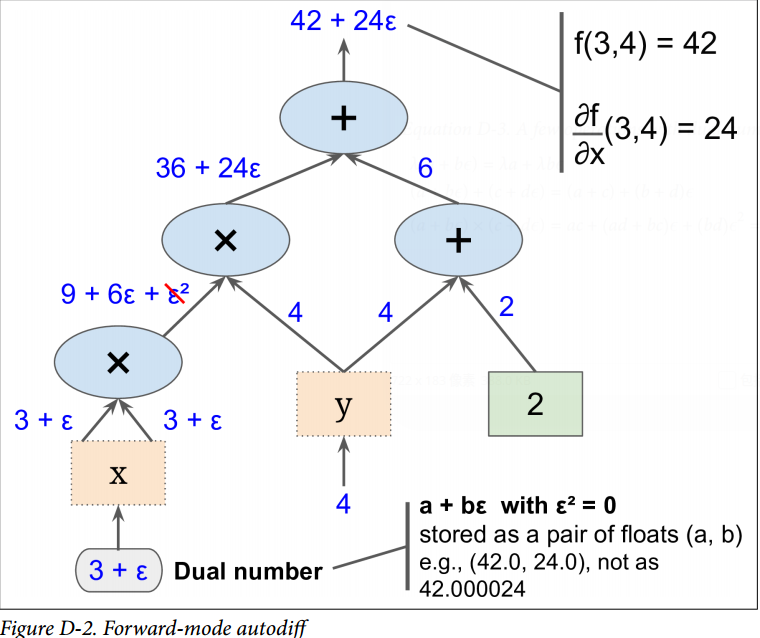
为了计算  我们不得不再遍历一遍计算图,但这次前馈的值为 。
所以前向自动微分比数值微分准确得多,但它遭受同样的缺陷:如果有 1000 个参数,那为了计算所有的偏导数,得历经计算图 1000 次。这正是反向自动微分耀眼的地方:计算所有的偏导数,它只需要遍历计算图 2 次。
## 反向自动微分
反向自动微分是 TensorFlow 采取的方案。它首先前馈遍历计算图(即,从输入到输出),计算出每个节点的值。然后进行第二次遍历,这次是反向遍历(即,从输出到输入),计算出所有的偏导数。图 D-3 展示了第二次遍历的过程。在第一次遍历过程中,所有节点值已被计算,输入是 。你可以在每个节点底部右方看到这些值(例如,)。节点已被标号,从 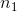 到 。输出节点是 。
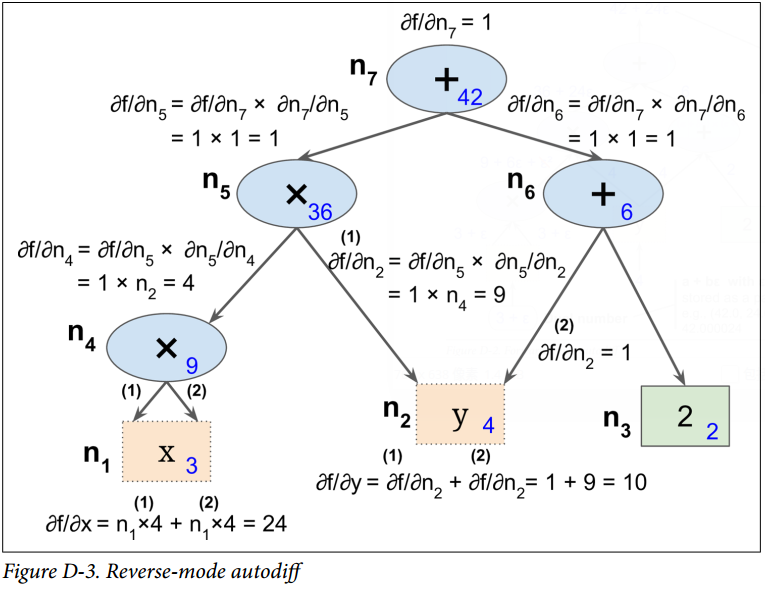
这个计算关于每个连续节点的偏导数的思想逐渐地从上到下遍历图,直到到达变量节点。为实现这个,反向自动微分强烈依赖于链式法则,如公式 D-4 所示。
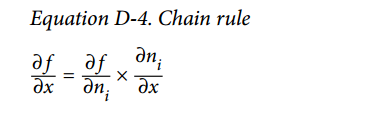
由于  是输出节点,即 ,所以 。
接着到了图的  节点:当  变化时, 会变化多少?答案是 。我们已经知道 ,因此我们只需要知道  就行。因为  是  的和,因此可得到 ,因此 。
现在前进到 :当  变化时, 会变化多少?答案是 。由于 ,我们可得到 ,所以 。
这个遍历过程一直持续,此时我们达到图的底部。这时我们已经得到了所有偏导数在点  处的值。在这个例子里,我们得到 。听起来很美妙!
反向自动微分是非常强大且准确的技术,尤其是当有很多输入参数和极少输出时,因为它只要求一次前馈传递加上一次反向传递,就可计算所有输出关于所有输入的偏导数。最重要的是,它可以处理任意代码定义的函数。它也可以处理那些不完全可微的函数,只要 你要求他计算的偏导数在该点处是可微的。
如果你在 TensorFlow 中实现了新算子,你想使它与现有的自动微分相兼容,那你需要提供函数,该函数用于构建一个子图,来计算关于新算子输入的偏导数。例如,假设你实现了一个计算其输入的平方的函数,平方算子 ,在这个例子中你需要提供相应的导函数 。注意这个导函数不计算一个数值结果,而是用于构建子图,该子图后续将计算偏导结果。这是非常有用的,因为这意味着你可以计算梯度的梯度(为了计算二阶导数,或者甚至更高阶的导数)。
