# 第十二章 `TreeMap`
> 原文:[Chapter 12 TreeMap](http://greenteapress.com/thinkdast/html/thinkdast013.html)
> 译者:[飞龙](https://github.com/wizardforcel)
> 协议:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
> 自豪地采用[谷歌翻译](https://translate.google.cn/)
这一章展示了二叉搜索树,它是个`Map`接口的高效实现。如果我们想让元素有序,它非常实用。
## 12.1 哈希哪里不对?
此时,你应该熟悉 Java 提供的`Map`接口和`HashMap`实现。通过使用哈希表来制作你自己的`Map`,你应该了解`HashMap`的工作原理,以及为什么我们预计其核心方法是常数时间的。
由于这种表现,`HashMap`被广泛使用,但并不是唯一的`Map`实现。有几个原因可能需要另一个实现:
哈希可能很慢,所以即使`HashMap`操作是常数时间,“常数”可能很大。
如果哈希函数将键均匀分配给子映射,效果很好。但设计良好的散列函数并不容易,如果太多的键在相同的子映射上,那么`HashMap`的性能可能会很差。
哈希表中的键不以任何特定顺序存储;实际上,当表增长并且键被重新排列时,顺序可能会改变。对于某些应用程序,必须或至少保持键的顺序,这很有用。
很难同时解决所有这些问题,但是 Java 提供了一个称为`TreeMap`的实现:
+ 它不使用哈希函数,所以它避免了哈希的开销和选择哈希函数的困难。
+ 在`TreeMap`之中,键被存储在二叉搜索树中,这使我们可以以线性时间顺序遍历键。
+ 核心方法的运行时间与`log(n)`成正比,并不像常数时间那样好,但仍然非常好。
在下一节中,我将解释二进制搜索树如何工作,然后你将使用它来实现`Map`。另外,使用树实现时,我们将分析映射的核心方法的性能。
## 12.2 二叉搜索树
二叉搜索树(BST)是一个树,其中每个`node`(节点)包含一个键,并且每个都具有“BST 属性”:
+ 如果`node`有一个左子树,左子树中的所有键都必须小于`node`的键。
+ 如果`node`有一个右子树,右子树中的所有键都必须大于`node`的键。
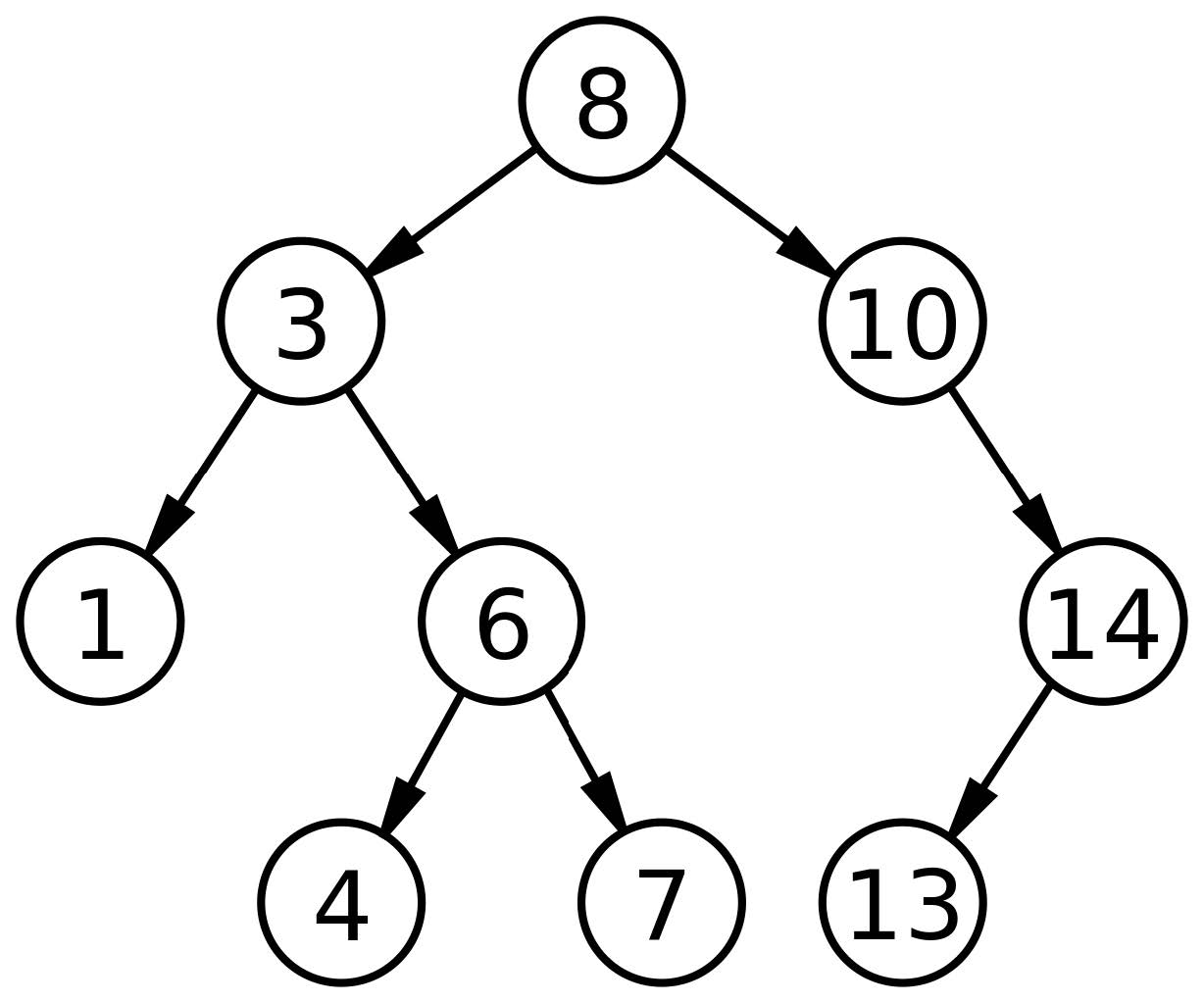
图 12.1:二叉搜索树示例
图 12.1 展示了一个具有此属性的整数的树。这个图片来自二叉搜索树的维基百科页面,位于 <http://thinkdast.com/bst>,当你做这个练习时,你会发现它很实用。
根节点中的键为`8`,你可以确认根节点左边的所有键小于`8`,右边的所有键都更大。你还可以检查其他节点是否具有此属性。
在二叉搜索树中查找一个键是很快的,因为我们不必搜索整个树。从根节点开始,我们可以使用以下算法:
+ 将你要查找的键`target`,与当前节点的键进行比较。如果他们相等,你就完成了。
+ 如果`target`小于当前键,搜索左子树。如果没有,`target`不在树上。
+ 如果`target`大于当前键,搜索右子树。如果没有,`target`不在树上。
在树的每一层,你只需要搜索一个子树。例如,如果你在上图中查找`target = 4`,则从根节点开始,它包含键`8`。因为`target`小于`8`,你走了左边。因为`target`大于`3`,你走了右边。因为`target`小于`6`,你走了左边。然后你找到你要找的键。
在这个例子中,即使树包含九个键,它需要四次比较来找到目标。一般来说,比较的数量与树的高度成正比,而不是树中的键的数量。
因此,我们可以计算树的高度`h`和节点个数`n`的关系。从小的数值开始,逐渐增加:
如果`h=1`,树只包含一个节点,那么`n=1`。
如果`h=2`,我们可以添加两个节点,总共`n=3`。
如果`h=3`,我们可以添加多达四个节点,总共`n=7`。
如果`h=4`,我们可以添加多达八个节点,总共`n=15`。
现在你可能会看到这个规律。如果我们将树的层数从`1`数到`n`,第`i`层可以拥有多达`2^(n-1)`个节点。`h`层的树共有`2^h-1`个节点。如果我们有:
```
n = 2^h - 1
```
我们可以对两边取以`2`为底的对数:
```
log2(n) ≈ h
```
意思是树的高度正比于`logn`,如果它是满的。也就是说,如果每一层包含最大数量的节点。
所以我们预计,我们可以以正比于`logn`的时间,在二叉搜索树中查找节点。如果树是慢的,即使是部分满的,这是对的。但是并不总是对的,我们将会看到。
时间正比于`logn`的算法是对数时间的,并且属于`O(logn)`的增长级别。
## 12.3 练习 10
对于这个练习,你将要使用二叉搜索树编写`Map`接口的一个实现。
这里是实现的开头,叫做`MyTreeMap`:
```java
public class MyTreeMap<K, V> implements Map<K, V> {
private int size = 0;
private Node root = null;
```
实例变量是`size`,它跟踪了键的数量,以及`root`,它是树中根节点的引用。树为空的时候,`root`是`null`,`size`是`0`。
这里是`Node`的定义,它在`MyTreeMap`之中定义。
```java
protected class Node {
public K key;
public V value;
public Node left = null;
public Node right = null;
public Node(K key, V value) {
this.key = key;
this.value = value;
}
}
```
每个节点包含一个键值对,以及两个子节点的引用,`left`和`right`。任意子节点都可以为`null`。
一些`Map`方法易于实现,比如`size`和`clear`:
```java
public int size() {
return size;
}
public void clear() {
size = 0;
root = null;
}
```
`size`显然是常数时间的。
`clear`也是常数时间的,但是考虑这个:当`root`赋为`null`时,垃圾收集器回收了树中的节点,这是线性时间的。这个工作是否应该由垃圾收集器的计数来完成呢?我认为是的。
下一节中,你会填充一些其它方法,包括最重要的`get`和`set`。
## 12.4 实现`TreeMap`
这本书的仓库中,你将找到这些源文件:
+ `MyTreeMap.java`包含上一节的代码,其中包含缺失方法的大纲。
+ `MyTreeMapTest.java`包含单元`MyTreeMap`的测试。
运行`ant build`来编译源文件。然后运行`ant MyTreeMapTest`。几个测试应该失败,因为你有一些工作要做!
我已经提供了`get`和`containsKey`的大纲。他们都使用`findNode`,这是我定义的私有方法;它不是`Map`接口的一部分。以下是它的起始:
```java
private Node findNode(Object target) {
if (target == null) {
throw new IllegalArgumentException();
}
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) target;
// TODO: FILL THIS IN!
return null;
}
```
参数`target`是我们要查找的键。如果`target`是`null`,`findNode`抛出异常。一些`Map`实现可以将`null`处理为一个键,但是在二叉搜索树中,我们需要能够比较键,所以处理`null`是有问题的。为了保持简单,这个实现不将`null`视为键。
下一行显示如何将`target`与树中的键进行比较。按照`get`和`containsKey`的签名(名称和参数),编译器认为`target`是一个`Object`。但是,我们需要能够对键进行比较,所以我们将`target`强制转换为`Comparable<? super K>`,这意味着它可以与类型`K`(或任何超类)的示例比较。如果你不熟悉“类型通配符”的用法,可以在 <http://thinkdast.com/gentut> 上阅读更多内容。
幸运的是,Java 的类型系统的处理不是这个练习的重点。你的工作是填写剩下的`findNode`。如果它发现一个包含`target`键的节点,它应该返回该节点。否则应该返回`null`。当你使其工作,`get`和`containsKey`的测试应该通过。
请注意,你的解决方案应该只搜索通过树的一条路径,因此它应该与树的高度成正比。你不应该搜索整棵树!
你的下一个任务是填充`containsValue`。为了让你起步,我提供了一个辅助方法`equals`,比较`target`和给定的键。请注意,树中的值(与键相反)不一定是可比较的,所以我们不能使用`compareTo`;我们必须在`target`上调用`equals`。
不像你以前的`findNode`解决方案,你的`containsValue`解决方案应该搜索整个树,所以它的运行时间正比于键的数量`n`,而不是树的高度`h`。
> 译者注:这里你可能想使用之前讲过的 DFS 迭代器。
你应该填充的下一个方法是`put`。我提供了处理简单情况的起始代码:
```java
public V put(K key, V value) {
if (key == null) {
throw new IllegalArgumentException();
}
if (root == null) {
root = new Node(key, value);
size++;
return null;
}
return putHelper(root, key, value);
}
private V putHelper(Node node, K key, V value) {
// TODO: Fill this in.
}
```
如果你尝试将`null`作为关键字,`put`则会抛出异常。
如果树为空,则`put`创建一个新节点并初始化实例变量`root`。
否则,它调用`putHelper`,这是我定义的私有方法;它不是`Map`接口的一部分。
填写`putHelper`,让它搜索树,以及:
+ 如果`key`已经在树中,它将使用新值替换旧值,并返回旧值。
+ 如果`key`不在树中,它将创建一个新节点,找到正确的添加位置,并返回`null`。
你的`put`实现的是时间应该与树的高度`h`成正比,而不是元素的数量`n`。理想情况下,你只需搜索一次树,但如果你发现两次更容易搜索,可以这样做:它会慢一些,但不会改变增长级别。
最后,你应该填充`keySet`。根据 <http://thinkdast.com/mapkeyset> 的文档,该方法应该返回一个`Set`,可以按顺序迭代键;也就是说,按照`compareTo`方法,升序迭代。我们在 8.3 节中使用的`HashSet`实现不会维护键的顺序,但`LinkedHashSet`实现可以。你可以阅读 <http://thinkdast.com/linkedhashset>。
我提供了一个`keySet`的大纲,创建并返回`LinkedHashSet`:
```
public Set<K> keySet() {
Set<K> set = new LinkedHashSet<K>();
return set;
}
```
你应该完成此方法,使其以升序向`set`添加树中的键。提示:你可能想编写一个辅助程序;你可能想让它递归;你也可能想要阅读 <http://thinkdast.com/inorder> 上的树的中序遍历。
当你完成时,所有测试都应该通过。下一章中,我会讲解我的解法,并测试核心方法的性能。
