# 查询管理器 [](http://files.devbean.net/images/2016/03/query_manager.png) **这部分是数据库的强大之处。**在这部分，一个写得有问题的查询语句会被转换成一个能够**快速**执行的代码。然后，代码被执行，结果返回给客户端管理器。这是多步操作： * 首先，查询语句会被**解析（parse）**，检查是不是合法。 * 然后，查询语句会被**重写（rewrite）**，移除没用的操作，增加一些预先的优化。 * 然后，查询语句会被**优化（optimize）**，改进性能，转换成一个执行和数据访问计划。 * 然后，这个计划会被**编译（compile）**， * 最后，这个计划会**被执行（execute）**。 在这部分，我不会对最后两点作过多的介绍，因为它们并不是那么重要。 在阅读完本部分时，如果你还想进一步学习，我推荐阅读下面的文章： * 有关基于成本的优化的原始研究论文（1979）：[Access Path Selection in a Relational Database Management System](http://www.cs.berkeley.edu/~brewer/cs262/3-selinger79.pdf)。这篇论文只有 12 页，只要有计算机科学知识的一般水平就足以理解。 * 一篇关于 DB2 9.X 如何优化查询的非常好并且很有深度的报告：[这里](http://infolab.stanford.edu/~hyunjung/cs346/db2-talk.pdf)。 * 一篇关于 PostgreSQL 如何优化查询的非常好的报告：[这里](http://momjian.us/main/writings/pgsql/optimizer.pdf)。这篇文章是最容易理解的，因为它主要是关于“给我看看在这些情形下，PostgreSQL 给出的查询计划是怎样的”以及“让我们看看 PostgreSQL 使用的算法”。 * 有关优化的 [SQLite 官方文档](https://www.sqlite.org/optoverview.html)。因为 SQLite 使用的规则都很简单，所以这篇文章比较“好懂”。并且，这是真正解释如何工作的唯一官方文档。 * 一篇关于 SQL Server 2005 如何优化查询的非常好的报告：[这里](https://blogs.msdn.com/cfs-filesystemfile.ashx/__key/communityserver-components-postattachments/00-08-50-84-93/QPTalk.pdf)。 * 有关 Oracle 12c 优化的白皮书：[这里](http://www.oracle.com/technetwork/database/bi-datawarehousing/twp-optimizer-with-oracledb-12c-1963236.pdf)。 * 来自《DATABASE SYSTEM CONCEPTS》作者的关于查询优化的 2 个理论课程：[这里](http://codex.cs.yale.edu/avi/db-book/db6/slide-dir/PPT-dir/ch12.ppt)以及[这里](http://codex.cs.yale.edu/avi/db-book/db6/slide-dir/PPT-dir/ch13.ppt)。着眼于磁盘 I/O 消耗，但是要求一定的计算机科学知识。 * 另外一个[理论课程](https://www.informatik.hu-berlin.de/de/forschung/gebiete/wbi/teaching/archive/sose05/dbs2/slides/09_joins.pdf)更好理解，但是仅着重于连接操作和磁盘 I/O。 ## 查询解析器 每一个 SQL 语句都会发送给解析器，后者将检查语句的语法。如果查询语句中有错误，解析器会拒绝该查询。例如，如果你写的是“SLECT …” 而不是“SELECT …”，那么处理就到此为止了。 但是，我们会深入探讨这一点。解析器还会检查关键字使用是不是顺序正确。例如，WHERE 出现在 SELECT 之前是不允许的。 然后，查询中的表格和字段都会被分析。解析器使用数据库元数据检查： * **表格是否存在** * 表格的**字段**是否存在 * 该字段是否允许**执行该操作**（例如，不允许将整型同字符串进行比较，不允许使用整型调用 substring() 函数） 然后，解析器检查你是不是有**权限**在查询中读取（或写入）数据表。再说一遍，这些表格的访问权限是由你的 DBA 设置的。 在解析期间，SQL 查询会被转换成一种内部的表示形式（通常是一棵树）。 如果所有一切正常，那么这个内部表示形式就会被发送给查询重写器。 ## 查询重写器 在这一步，我们有一个查询的内部表示。重写器的目的是： * 预优化查询 * 避免不必要的操作 * 帮助优化器找到最好的可行方案 重写器会在查询语句上执行一系列已知的规则。如果查询符合某一规则的模式，那么该规则就会被应用到这个查询，查询会被重写。下面是一组简单的（可选）规则列表： * **视图合并**：如果查询中使用了视图，那么视图会被转换成该视图的 SQL 语句。 * **子查询扁平化**：子查询会明显增加优化的难度，因此，重写器会尝试修改带有子查询的查询，以便去除子查询。 例如， ~~~ SELECT PERSON.* FROM PERSON WHERE PERSON.person_key IN (SELECT MAILS.person_key FROM MAILS WHERE MAILS.mail LIKE 'christophe%'); ~~~ 可以替换为 ~~~ SELECT PERSON.* FROM PERSON, MAILS WHERE PERSON.person_key = MAILS.person_key and MAILS.mail LIKE 'christophe%'; ~~~ * **移除不必要的操作**：例如，如果你在有 UNIQUE 约束来避免数据出现重复的地方使用了 DISTINCT，那么，DISTINCT 关键字就会被移除。 * **移除冗余连接**：如果你有两个相同的连接，可能是因为在视图中已经暗含了一个连接条件，或者是由于传递律出现了一个没有用的连接，该连接就会被移除。 * **常量算术计算**：如果你的语句需要计算，那么，计算结果就在重写中就获得。例如，WHERE AGE > 10+2 会传换成 WHERE AGE > 12；TODATE(“日期”) 则会直接转换成所需的日期格式。 * **（高级）分区裁剪**：如果你使用的是分区表，重写器会找出使用了哪些分区。 * **（高级）物化视图重写**：如果物化视图符合查询语句中谓词的子集，重写器会检查视图是不是最新的，并且修改查询优先使用物化视图而不是原始表。 * **（高级）自定义规则**：如果有自定义规则修改查询（比如 Oracle 策略），重写器会执行这些规则。 * **（高级）OLAP 变形**：应用分析/窗口函数，star join，rollup 函数等（但是我不确定这部分是由重写器还是优化器完成的，由于这部分处理非常相近，所以很可能是依赖于数据库的实现）。 重写后的查询会发送给查询优化器，这时候，有趣的才真正开始！ ## 统计 在我们学习数据库如何优化查询之前，我们需要先讨论下**统计**。因为没有统计的话，数据库是很愚蠢的。如果你不告诉数据库去分析下它们自己的数据，它们是不会主动去做的，会得到一个很糟糕的假设。 但是，数据库需要什么类型的信息？ 我需要（简短地）讨论下数据库和操作系统是如何存储数据的。数据存储的最小单位是**页（page）**或者块（block），默认是 4 或 8 KB。这意味着如果你只需要 1 KB，它依然会占用整个页。如果一个页是 8 KB，那么你就会浪费 7 KB。 回到统计！当你要求数据库收集统计信息时，它会计算： * 表格中的行数或页数 * 表格中每一列： * 不同的数据值 * 数据值的长度（最大值、最小值、平均值） * 数据范围的信息（最大值、最小值、平均值） * 表格索引的信息 **这些统计可以帮助优化器估算查询中的磁盘 I/O、CPU 和内存使用。** 每一列的统计都很重要。例如，如果 PERSON 表需要连接 2 列：LAST_NAME 和 FIRST_NAME。通过统计，数据库就会知道 FIRST_NAME  列只有 1000 个不同的值，而 LAST_NAME 则有 1000000 个不同值。因此，数据库会使用 LAST_NAME, FIRST_NAME 连接数据，而不是 FIRST_NAME,LAST_NAME，这会产生更少的比较步骤，因为 LAST_NAME 一般不会相同，有可能只需要比较 2（或 3）个字符就可以了。 但是这些只是基本统计。你可以要求数据库计算高级统计，称为**直方图（histograms）**。直方图代表列内部值的分布。例如： * 最常见的值 * 分位数 * … 这些额外统计将帮助数据库找到更好的查询计划。这种统计对于相等谓词（例如，WHERE AGE = 18）或范围谓词（例如，WHERE AGE > 10 AND AGE < 40）尤其有效，因为数据库可以获得有关这两种谓词数据行分布的更好信息（注意，这种概念的专业术语是选择性 selectivity）。 统计信息存储在数据库的元数据中。例如，你可以在下面位置看到（非分割）表的统计信息： * Oracle 数据库在 USER/ALL/DBA_TABLES 和 USER/ALL/DBA_TAB_COLUMNS * DB2 数据库在 SYSCAT.*TABLES* 和 *SYSCAT.COLUMNS* **统计信息必须及时更新。**最糟糕的是，当数据库表实际有 1000000 行时，它却认为只有 500 行。统计的缺点是，需要**花费大量时间进行计算**。这也就是为什么大多数数据库并不会自动计算统计信息。当数据库有百万级别的数据量时，计算统计信息会非常困难。在这种情况下，你可以选择只计算基本统计或计算数据样本库的统计。 例如，我曾经在一个项目工作，该项目中每一个表的数据量达到亿级别。我选择其中 10% 计算统计数据，这节省了大量时间。但是，最终结果表明这是一个错误的决定，因为 Oracle 10G 选择的这 10% 恰恰是一个特殊表的特殊字段，根本不能代表其余 100% 的数据（对于 1 亿的数据量，这并不经常发生）。这个错误的统计使得一个本应只有 30 秒的查询消耗了近 8 小时。查找问题的过程简直就是噩梦。这个故事说明了统计是有多么重要。 注意，每种数据库都会有特殊的高级统计。如果你想要了解更多，可以阅读数据库文档。就像前面说的，当我试图了解统计是如何使用的时候，发现的最好的官方文档就是[来自 PostgreSQL 的一篇](http://www.postgresql.org/docs/9.4/static/row-estimation-examples.html)。 ## 查询优化器 [](http://files.devbean.net/images/2016/03/McDonalds_CBO.jpg) 所有现代数据库都使用**基于成本的优化（Cost Based Optimization，CBO）**来优化查询。其思路是，为每一个操作添加一个成本，通过使用成本最低的操作链降低查询成，最终获得结果。 为了弄清楚成本优化器是如何工作的，我觉得最好的方法是“感受”这个任务背后的复杂性。在这部分，我将表述连接两张表的三种通用方法，我们很快就会看到每一个简单的连接查询都是一个优化的噩梦。在此之后，我们将看到真正的优化器是如何进行这个工作的。 对于这些连接，我着眼于它们的时间复杂度，但是**数据库优化器会计算其 CPU 成本、磁盘 I/O 成本以及所需内存**。时间复杂度和 CPU 成本的区别在于，前者是非常粗略的（对于那些像我一样懒的人来说）。对于 CPU 成本，我需要计算每一个操作，比如一次加法，一条“if 语句”，一次乘法，一次便利等。另外： * 每一条高级代码操作都需要几条低级 CPU 操作。 * 对于 Intel Core i7、Item Pentium 4 或者 AMD 的 CPU 而言，每一个 CPU 操作的成本都不相同（其术语是 CPU 周期）。换句话说，CPU 操作的成本取决于 CPU 架构。 使用时间复杂度更简单（至少对于我来说是这样），使用时间复杂度我们依然能够获得 CBO 的概念。有时我也会提到磁盘 I/O，因为这也是一个重要概念。时刻记住，**瓶颈在磁盘 I/O 所消耗的时间，而不是 CPU 消耗的**。 ### 索引 在我们介绍 B+ 树的时候，我们讨论过索引。记住，**索引已经排好序了**。 仅供参考：数据库还有其它类型的索引，比如**位图索引（bitmap indexes）**。它们与 B+ 树索引消耗的 CPU 周期、磁盘 I/O 和内容都不相同。 另外，如果可以改善执行计划的成本，很多现代数据库可以**为当前插件动态创建临时索引**。 ### 访问路径 在应用连接运算符之前，首先你需要获得数据。下面是你能够如何获得数据。 注意：由于访问路径真正的问题在于磁盘 I/O，因此我不会过多讨论时间复杂度。 #### 完整扫描 如果你阅读过执行计划，你一定见过完整扫描（**full scan**，或者就叫 scan）这个词。完整扫描就是数据库读取整张表或索引。**考虑到磁盘 I/O，很明显，对于整张表的完整扫描的成本要远远高于对于索引的完整扫描。** #### 范围扫描 其它类型的扫描有**索引范围扫描（index range scan）**。当你使用谓词，比如“WHERE AGE > 20 AND AGE <40”时，就会使用索引范围扫描。 当然，为了使用索引范围扫描，你需要在 AGE 字段添加索引。 在前面部分，我们已经了解到，范围查询的时间成本可能会有 log(N) +M，其中，N 是索引数据量，M 是落在这个范围的行数的估计值。**多亏了统计数据，N 和 M 都是已知的**（注意，M 就是谓词 AGE >20 AND AGE<40 的选择率）。另外，对于范围扫描，你不需要只读完整的索引，因此要**比完整扫描的磁盘 I/O 成本小得多**。 #### 唯一扫描 如果你只需要从索引获取一个值，可以使用**唯一扫描（unique scan）**。 #### 通过 row id 访问 大多数时间，如果数据库使用索引，它就得找到关联到索引的那些行。为了达到这一目的，数据库会使用 row id 访问。 例如，如果你的语句如下： ~~~ SELECT LASTNAME, FIRSTNAME from PERSON WHERE AGE = 28 ~~~ 如果 age 列有索引，优化器会使用索引找到所有 28 岁的人，然后会请求表中关联的那些行。这是因为索引只包含了年龄的信息，但是你却想要获取 lastname 和 firstname。 但是，如果你的语句如下： ~~~ SELECT TYPE_PERSON.CATEGORY from PERSON, TYPE_PERSON WHERE PERSON.AGE = TYPE_PERSON.AGE ~~~ PERSON 的索引用于连接 TYPE_PERSON，但是 PERSON 表却不会使用 row id 访问，因为你并没有请求这个表的数据。 对于少量访问，这是可行的，但这个操作的真正问题在于磁盘 I/O。如果你需要通过 row id 访问很多数据，数据库可能会选择使用完整扫描。 #### 其它路径 我并没有阐述所有访问路径。如果你想了解更多，可以阅读 [Oracle 文档](https://docs.oracle.com/database/121/TGSQL/tgsql_optop.htm)。对于其它数据库，文档的名字可能会有歧义，但是其背后的原理是相通的。 ### 连接运算符（join） 现在我们知道了如何获得数据，然后，让我们将数据连接起来！ 我会介绍三种通用连接运算符：归并连接、哈希连接和嵌套循环连接。但在此之前，我需要介绍一个新的术语：**内关系（inner relation）**和**外关系（outer relation）**。一个关系可以是 * 一个表 * 一个索引 * 来自上一步操作的中间结果（例如上一个连接的结果） 当你连接两个关系时，连接算法会分别管理两个关系。在本文剩下的部分，我会假设： * 外关系是左数据集 * 内连接是右数据集 例如，A JOIN B 是 A 和 B 的连接，其中，A 是外连接，B 是内连接。 大多数情况下，**A JOIN B 的成本与 B JOIN A 并不相同**。 **在这一部分，我同样假设外连接有 N 个元素，内连接有 M 个元素**。时刻记住，真正的优化器可以通过统计知道 N 和 M 的值。 注意，N 和 M 是联系的基数。 #### 嵌套循环连接（nested loop join） 嵌套循环连接是最简单的一个。 [](http://files.devbean.net/images/2016/03/nested_loop_join.png) 其思路是： * 对于外关系的每一行 * 检查内关系中的所有行，看是不是有行能够匹配 伪代码如下： ~~~ nested_loop_join(array outer, array inner) for each row a in outer for each row b in inner if (match_join_condition(a, b)) write_result_in_output(a, b) end if end for end for ~~~ 因为这里有两层循环，所以**时间复杂度是 O(N*M)**。 从磁盘 I/O 方面，对于外关系 N 行的每一行，内层循环都需要从内关系读取 M 行。这个算法需要从磁盘读取 N + N * M 行。但是，如果内关系足够小，那么就可以把所有关系放在内存，这样就只需要 M +N 次读取。根据这样的修改，**内关系必须是最小的一个**，因为只有这样才有更多机会放入内存。 从时间复杂度方面，这样并没有什么不同，但是从磁盘 I/O 方面，这种方式只需要读取两种关系一次。 当然，内关系可以替换为索引，这样对磁盘 I/O 更有利。 由于这个算法非常简单，对于那些不能完全读入内存的内关系而言，还有一个对磁盘 I/O 更友好的版本。其思路是这样的： * 不是一行一行读取关系 * 按照批次读取关系，在内存中始终保存两个批次的行（每个关系都保留 2 个批次） * 在两个批次内部比较行，保留匹配的行 * 然后，从磁盘加载新的批次，再进行比较 * 如此进行下去，知道没有批次可供加载 下面是算法伪代码： ~~~ // 改进版本，减少磁盘 I/O。 nested_loop_join_v2(file outer, file inner) for each bunch ba in outer // 现在 ba 在内存中 for each bunch bb in inner // 现在 bb 在内存中 for each row a in ba for each row b in bb if (match_join_condition(a,b)) write_result_in_output(a,b) end if end for end for end for end for ~~~ **使用这个版本，时间复杂度相同，但是磁盘访问次数有所减少：** * 之前的版本，算法需要 N + N * M 次磁盘访问（每次访问读取一行） * 新的版本，磁盘访问数变为 number_of_bunches_for(outer) + number_of_ bunches_for(outer) * number_of_ bunches_for(inner) * 增加每一批次的大小，就能降低磁盘访问次数 注意：虽然每一次磁盘访问都可以加载比上述算法更多的数据，但是由于数据是顺序访问的（机械硬盘真正的问题是获得第一组数据所需时间），因此影响并不会很大。 #### 哈希连接 哈希连接要比嵌套循环连接复杂得多，但是在很多情形下，它的性能要比后者好得多。 [](http://files.devbean.net/images/2016/04/hash_join.png) 哈希连接的思路是： 1. 从内关系获取所有元素 2. 构建内存中的哈希表 3. 依次获取外关系中的所有元素 4. 计算每一个元素的哈希值（使用哈希表的哈希函数），找到与内关系关联的桶 5. 检查桶中元素和外表中的元素是不是匹配 关于时间复杂度，我需要作一些假定以简化问题： * 内关系分为 X 个桶 * 对于两个关系，哈希函数都可以均匀地散列哈希值。换句话说，这些桶的大小相同 * 外关系中的一个元素与桶中所有元素的匹配过程消耗只与桶中的元素数目有关 其时间复杂度是 (M/X) * N + cost_to_create_hash_table(M) + cost_of_hash_function*N 如果哈希函数创建足够小的桶，那么，**时间复杂度就是 O(M+N)**。 下面的哈希连接的版本对内存更友好，但是不利于磁盘 I/O。这一次： 1. 同时计算内关系和外关系的哈希表 2. 将计算出的哈希值存入磁盘 3. 然后按照桶依次比较两个关系（现将一个加载到内存，然后依次读取另外一个） #### 归并连接 **归并连接是唯一获得排序结果的连接。** 注意：在这个简化的归并连接中，不存在内表或外表；它们的角色是一致的。但是，实际实现是有区别的，例如，当处理复制时。 归并连接可以分为两步： 1. （可选的）排序连接操作：两个输入都按照连接键进行排序 2. 归并连接操作：将排好序的输入合并在一起 *排序* 我们已经讨论了归并排序，在这个情形下，归并排序是一个不错的算法（但是如果内存不是问题的话，这并不是最好的算法）。 但是，有时数据集已经排好序了，例如： * 表自然地排序了，例如在连接条件上使用索引组织的表 * 如果在连接条件上，这个关系是一个索引 * 如果这个连接应用在一个中间结果上，而这个中间结果已经在查询处理阶段排好序了 *归并连接* [](http://files.devbean.net/images/2016/04/merge_join.png) 这一步非常像我们之前见过的归并排序的归并操作。但是这一次我们并不是从每个关系中取出每一个元素，而是从每个关系中取出相同元素。其思想是： 1. 比较两个关系中的当前元素（第一次时，当前元素就是第一个元素） 2. 如果相同，将两个元素放进结果集，然后获取两个关系中的下一个元素 3. 如果不相同，从较小元素所在关系中取出下一个元素（因为下一个元素可能会相同） 4. 重复以上 3 步，直到其中一个关系到达最后一个元素 因为两个关系都是排好序的，因此这种操作是可行的。你不需要在这些关系中“后退”。 这个算法是一个简化版本，因为它没有处理两个数组中相同数据出现多次的情况（也就是多次匹配）。真实的版本会更复杂一些，但也不会复杂太多，因此我选择了一个相对简单的版本。 如果两个关系都已经排好序，那么**时间复杂度就是 O(N+M)**。 如果两个关系都需要排序，那么时间复杂度就是两个关系排序的消耗：**O(N * Log(N) + M * Log(M))**。 对于计算机专业技术人员，下面是一个能够处理多次匹配的可行算法（虽然我也不是 100% 确保算法正确性）： ~~~ mergeJoin(relation a, relation b) relation output integer a_key:=0; integer b_key:=0; while (a[a_key]!=null or b[b_key]!=null) if (a[a_key] < b[b_key]) a_key++; else if (a[a_key] > b[b_key]) b_key++; else //Join predicate satisfied //i.e. a[a_key] == b[b_key] //count the number of duplicates in relation a integer nb_dup_in_a = 1: while (a[a_key]==a[a_key+nb_dup_in_a]) nb_dup_in_a++; //count the number of duplicates in relation b integer dup_in_b = 1: while (b[b_key]==b[b_key+nb_dup_in_b]) nb_dup_in_b++; //write the duplicates in output for (int i = 0 ; i< nb_dup_in_a ; i++) for (int j = 0 ; i< nb_dup_in_b ; i++) write_result_in_output(a[a_key+i],b[b_key+j]) a_key=a_key + nb_dup_in_a-1; b_key=b_key + nb_dup_in_b-1; end if end while ~~~ #### 哪个最好？ 如果有最好的连接方式，就不会有这么多种了。这个问题很难回答，因为有很多因素在里面： * **可用内存总数**：没有足够了内存，就基本可以跟强大的哈希连接说拜拜了（至少对完全内存中的哈希连接） * **两个数据集的大小**：例如，如果你有一张大表和一个很小的表，那么，嵌套循环连接要比哈希连接快一些，因为哈希连接需要计算哈希值。如果你的两张表都很大，那么，嵌套循环连接会消耗非常多的 CPU。 * **是不是有索引**：对于归并连接，两个 B+ 树索引绝对是一个好主意。 * 如果**结果需要排序**：即使你的数据集没有排序，你还是可能想使用代价昂贵的归并连接（使用排序），因为最终结果是排好序的，你可以将这个结果交给另外的归并连接（或者是由于查询语句使用 ORDER BY/GROUP BY/DISTINCT 等隐式或显式要求了结果排序）。 * 如果**关系已经排好序**：这种情况下，归并连接是最好的选择。 * 你正在使用的连接类型：是不是** equijoin** （例如 tableA.col1 = tableB.col2）？是不是 **inner join**、**outer join**、**cartesian product** 或者 **self-join**？某些连接不适用与特定情形。 * **数据的分布**：如果连接条件中的数据是**不均衡的（skewed）**，例如，你需要使用人名中的姓氏连接，但是很多人都有相同的姓，使用哈希连接就是一场灾难，因为哈希函数计算出来的桶是非常不均衡的。 * 如果你需要在**多线程或多进程**情形下进行连接。 更多信息，可以阅读 [DB2](https://www-01.ibm.com/support/knowledgecenter/SSEPGG_9.7.0/com.ibm.db2.luw.admin.perf.doc/doc/c0005311.html)、[ORACLE](http://docs.oracle.com/cd/B28359_01/server.111/b28274/optimops.htm#i76330) 或 [SQL Server](https://technet.microsoft.com/en-us/library/ms191426(v=sql.105\).aspx) 的文档。 ### 简单的例子 我们已经见识到了 3 种类型的连接操作。 现在，假设我们需要连接 5 张表来获取一个人的全部信息。*一个人*有： * 多个手机（MOBILES） * 多个邮箱（MAILS） * 多个地址（ADRESSES） * 多个银行账户（BANK_ACCOUNTS） 换句话说，我们需要能够快速地找出下面查询的结果： ~~~ SELECT * from PERSON, MOBILES, MAILS,ADRESSES, BANK_ACCOUNTS WHERE PERSON.PERSON_ID = MOBILES.PERSON_ID AND PERSON.PERSON_ID = MAILS.PERSON_ID AND PERSON.PERSON_ID = ADRESSES.PERSON_ID AND PERSON.PERSON_ID = BANK_ACCOUNTS.PERSON_ID ~~~ 作为一个查询优化器，我必须找到最好的途径来处理数据。但是，这里有两个问题： * 针对每一个连接，我需要选择使用哪种类型？ 我有 3 种类型可供选择（哈希连接、归并连接和嵌套连接），每种类型可以使用 0 个、1 个或者 2 个索引（并不是说有不同类型的索引）。 * 我应该按照怎样的顺序计算连接？ 例如，下面的图显示了 4 张表的 3 个连接的不同计划： [](http://files.devbean.net/images/2016/04/join_ordering_problem.png) 现在我有下面几个选择： * 1) 暴力实现 利用数据库统计，我**计算得出每种计划的成本**，选择最好的一个。但是这有很多可能性。对于一个给定的连接顺序，每种连接有 3 种可能：哈希连接、归并连接和嵌套连接。那么，对于给定的连接顺序，一共有 34 种可能性。连接顺序是[二叉树上面的排序问题](https://en.wikipedia.org/wiki/Catalan_number)，有 (2*4)!/(4+1)! 种排序。对于这个简单的问题，我们有 34*(2*4)!/(4+1)! 种可能性。 用“人话”来说，一共有 27 216 种可能的计划。现在，如果我增加归并连接可以使用的 B+ 树索引数为 0、1 或 2，可能的计划数变成了 210 000。我记得我说过这个查询是*非常简单*的吗？ * 2) 哭着说不干了 这的确非常解气，但是你没法拿到你要的结果，我也需要花钱去缴我的账单。 * 3) 我只试几个计划，从中选择一个成本最低的 因为我不是超人，我没办法计算每一个计划的成本。所以，我**随机地选择所有可能的计划的一个子集**，计算其成本，给你这个子集中最好的计划。 * 4) 我应用一个非常聪明的**能够减少可能的计划数的规则** 有两种类型的规则： “逻辑”规则，用于移除没什么用的可能计划，但是并不能过滤掉大部分可能的计划。例如：“嵌套循环连接的内关系必须是最小的数据集”。 我接受不去找到最好的解决方案，而是应用积极的规则来减少可能性的数量。例如，“如果关系很少，使用嵌套循环连接，不使用归并连接和哈希连接”。 在这个简单的例子中，最终我的结果还会有很多种可能性。但是，**在真实的查询中，还有其它的关系运算符**，例如 OUTER JOIN、CROSS JOIN、GROUP BY、ORDER BY、PROJECTION、UNION、INTERSECT、DISTINCT … **这意味着甚至有更多可能性。** 那么，数据库是怎么做的？ ### 动态规划、贪心算法和启发式算法 关系数据库会尝试我前面说的各种实现。优化器的真正工作是在有限时间内找出一个好的解决方案。 **大多数时间，优化器并不是找到最好的解决方案，而是一个“好的”解决方案。** 对于小的查询，暴力实现是可能的。但是，还有一种方法可以避免不必要的计算，从而使得一些中级查询也可以使用暴力实现。这种方法叫做动态规划。 #### 动态规划 这个词背后的思想是，大部分执行计划都是相似的。如果你看一下下面的计划： [](http://files.devbean.net/images/2016/04/overlapping_trees.png) 这些计划都共享了相同的 (A JOIN B) 子树。因此，不需要在每一个计划都计算这个子树的成本，我们只需要计算一次，将计算所得的成本保存下来，当再次见到这个子树时，复用这个计算结果即可。正式的说法是，我们面对的是一个重叠问题。为避免中间结果的额外计算，我们使用了记忆技术。 利用这一技术，我们的时间复杂度不是 (2*N)!/(N+1)!，“仅仅”是3N。在我们前面四个连接的例子中，这意味着可能性将从 336 降低到 81。如果你的查询更大（比如 **8 个连接的查询**，这其实也算不上大），这意味着可能性**从57 657 600 降低到 6561**。 对于计算机专业人士，我[在前面提到过的正式课程](http://codex.cs.yale.edu/avi/db-book/db6/slide-dir/PPT-dir/ch13.ppt)中找到一个算法。我不会解释这个算法，所以，如果你懂动态规划或者对算法有兴趣的话，可以仔细阅读下面的算法（我已经警告过你了！）： ~~~ procedure findbestplan(S) if (bestplan[S].cost infinite) return bestplan[S] // else bestplan[S] has not been computed earlier, compute it now if (S contains only 1 relation) set bestplan[S].plan and bestplan[S].cost based on the best way of accessing S /* Using selections on S and indices on S */ else for each non-empty subset S1 of S such that S1 != S P1= findbestplan(S1) P2= findbestplan(S - S1) A = best algorithm for joining results of P1 and P2 cost = P1.cost + P2.cost + cost of A if cost < bestplan[S].cost bestplan[S].cost = cost bestplan[S].plan = “execute P1.plan; execute P2.plan; join results of P1 and P2 using A” return bestplan[S] ~~~ 对于更大的查询，你还是可以继续使用动态规划算法，但是还可以有另外的规则（启发式算法）来移除一些可能性： * 如果我们分析唯一类型的计划（例如左深树），我们可以做到 n*2n 而不是 3n [](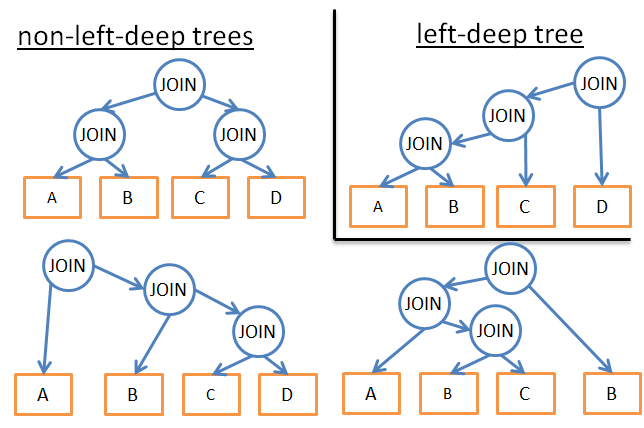http://files.devbean.net/images/2016/04/left-deep-tree.png) * 如果我们添加逻辑规则来避免某些模式的计划（例如，“如果一张表对于给定谓词包含一个索引，那么就要在索引而不是表上应用归并连接”），那么就可以减少可能性的数量而不会影响到最好可能的解决方案。 * 如果我们在工作流添加规则（例如，“在其它关系操作*之前*应用连接”），同样会减少很多可能性。 * … #### 贪心算法 为了处理非常大的查询，或者为了快速获得答案（针对不是那么快的查询），需要使用另外一种类型的算法——贪心算法。 贪心算法的思路是，利用某种规则（或**启发式**）构建一种渐进的查询计划。根据这种规则，贪心算法每次找到一个问题的最佳解的一个步骤。算法从一个 JOIN 开始查询计划。然后，在之后的每一步种，算法按照相同规则，向查询计划增加一个新的 JOIN。 下面我们看一个简单的例子。假设我们有一个查询，包含五张表（A，B，C，D，E）四个连接。为了简化问题，我们只考虑嵌套连接。我们使用的规则是“使用最低成本的连接”。 * 我们从五张表中任意一个开始（例如，从 A 开始） * 计算与 A 的每一个连接的成本（A 作为内关系或外关系） * 发现 A JOIN B 是最低成本 * 然后计算与 A JOIN B 结果关联的每一个连接的成本（A JOIN B 作为内关系或外关系） * 找到 (A JOIN B) JOIN C 是最低成本 * 然后计算与 (A JOIN B) JOIN C 结果关联的每一个连接的成本… * …. * 最后，找到计划 (((A JOIN B) JOIN C) JOIN D) JOIN E) 由于我们是随机从 A 开始，因此也可以为 B、C、D 和 E 应用相同的算法。最后，我们找到了拥有最低成本的计划。 人们给使用这种方法的算法取了一个名字：[最近邻居算法](https://en.wikipedia.org/wiki/Nearest_neighbour_algorithm)。 我不会展开阐述，只说结论，通过良好的建模和 N*log(N) 的排序，该问题可以[很容易解决](http://www.google.fr/url?sa=t&rct=j&q=&esrc=s&source=web&cd=5&cad=rja&uact=8&ved=0CE0QFjAEahUKEwjR8OLUmv3GAhUJuxQKHdU-DAA&url=http%3A%2F%2Fwww.cs.bu.edu%2F~steng%2Fteaching%2FSpring2004%2Flectures%2Flecture3.ppt&ei=hyK3VZGRAYn2UtX9MA&usg=AFQjCNGL41kMNkG5cH)。**这个算法的时间复杂度是 O(N*log(N))，相比而言，完全动态规划算法的时间复杂度是 O(3N)。**如果你有一个 20 个连接的大查询，这意味着 26 比 3 486 784 401，这个差距非常巨大！ 这个算法的问题是，我们假设如果能够一直找到两个表直接的最好连接，并且在此基础上增加新的连接，依然能够保持最好的成本。但是： * 在 A、B、C 三者之间，即便 A JOIN B 给出最好成本 * (A JOIN C) JOIN B 依然可能比 (A JOIN B) JOIN C 还要好 为改进结果，你可以使用不同规则多次运行贪心算法，保留最好的计划。 #### 其它算法 [如果你已经厌倦了算法，直接跳到下一部分就好了。下面我将要介绍的内容与本文其它部分没有太大关系。] 找到最佳解决方案一直是计算机科学家的热门研究方向。他们试图为更多精确的问题或模式找到更好的解决方案。例如： * 如果查询是星连接（就是多个连接查询的中心位置），有些数据库会使用特殊的算法 * 如果查询是并行的，有些数据库也会使用特殊的算法 * … 另外的算法同样有被研究，以便取代大查询的动态规划。贪心算法属于一个称为**启发式算法**的更大的算法家族。贪心算法遵循一个规则（或启发），持有上一步发现的解决方案，在当前步骤将这个解决方案“追加”以便获得新的解决方案。有些算法则是遵循规则，每一步都会应用规则，但是不会始终保存上一步找到的最佳解决方案。这种算法被称为启发式算法。 例如，**遗传算法**依照规则，但是并不始终保存上一步的最好结果： * 一个能够表示全查询计划的可能解决方案 * 在每一步不只保存一个，而是保存 P 个解决方案 * 0) P 个查询计划是随机创建的 * 1) 只有最好成本的计划被保留 * 2) 这些最好的计划混合起来，创建 P 个新的计划 * 3) 这些 P 个新计划中的某些被随机改变 * 4) 重复 1，2，3 步 T 次 * 5) 在最后一次循环之后，找到 P 个计划的最佳计划 循环越多，你能获得的计划就会越好。 听起来就像魔法一样？不，这是自然法则：适者生存！ 仅供参考，遗传算法在 [PostgreSQL](http://www.postgresql.org/docs/9.4/static/geqo-intro.html) 有实现，但是我不确定是不是默认使用了该算法。 数据库还使用了一些别的启发式算法，例如模拟退火算法、迭代改进算法、两阶段优化… 但是我不确定这些算法是不是已经应用在企业级数据库中，还是仅仅出现在研究型的数据库中。 更多信息可以阅读下面的论文，这篇论文列举了更多算法：[Review of Algorithms for the Join Ordering Problem in Database Query Optimization](http://www.acad.bg/rismim/itc/sub/archiv/Paper6_1_2009.PDF)。 ### 真实的优化器 [你可以直接跳到后面的章节，这部分也不是非常重要] 但是，我们啰嗦了半天，都是理论上的。因为我是一个开发人员，不是研究学者，我喜欢**具体的例子**。 下面看 [SQLite 优化器](https://www.sqlite.org/optoverview.html)是如何工作的。这是一个轻量级数据库，使用了基于额外规则的贪心算法的简单优化，用于限定可能数： * SQLite 从不重新排序 CROSS JOIN 运算符中的表 * **连接使用嵌套连接实现** * 外连接始终按照出现的顺序 * … * 在 3.8.0 之前的版本，**SQLite 使用“最近邻居”贪心算法检索最佳查询计划** 等一下… 我们已经见到了这个算法了！真巧！ * 从 3.8.0 （2015 年发布）开始，SQLite 使用“N 个最近邻居”**贪心算法**检索最佳查询计划 我们看看另外的优化器是怎么工作的。IBM DB2 和其它所有企业级数据库一样，我将介绍 DB2，因为这是我转换到大数据之前唯一真正使用过的数据库。 如果我们阅读[官方文档](https://www-01.ibm.com/support/knowledgecenter/SSEPGG_9.7.0/com.ibm.db2.luw.admin.perf.doc/doc/r0005278.html)，我们就会发现 DB2 优化器允许你使用 7 个不同级别的优化： * 使用贪心算法处理连接 * 0 – 最小优化，使用索引扫描和嵌套循环连接，避免某些查询重写 * 1 – 低优化 * 2 – 全优化 * 使用动态规划处理连接 * 3 – 中度优化，粗略近似 * 5 – 全优化，使用基于启发式算法的所有技术 * 7 – 全优化，与 5 类似，但是不使用启发式算法 * 9 – 最大优化，不遗余力**考虑所有可能的连接顺序，包括笛卡尔积**。 我们可以发现，**DB2 使用了贪心算法和动态规划**。当然，他们不会告诉你启发式算法的细节，因为查询优化器是一个数据库强大所在。 仅供参考，**默认级别是 5**。优化器默认使用下面的特性： * **使用全部可用的统计**，包括快速统计值和分位数统计 * **应用所有查询重写规则**（包括物化查询表路由），除了仅适用于少数情况的计算密集型规则 * **使用动态规划算法连接枚举**，包括： * 限制使用内关系组合 * 限制针对星模式使用笛卡尔积查询表 * 考虑大范围访问函数，包括列举预取（我们会在后文介绍这个词的含义），索引 AND（针对索引的特殊操作）和物化查询表路由 默认的，**DB2 针对连接排序，使用有限制的启发式动态规划**。 其它条件（GROUP BY, DISTINCT…）则使用简单规则处理。 ### 查询计划缓存 由于创建计划要花费一定时间，大部分数据库都会将计划保存到**查询计划缓存**。这是一个复杂的话题，因为数据库需要知道什么时候更新过时的计划。其思路是，使用一个阈值，如果表的统计数据发生的改变超过了阈值，那么有关这个表的查询计划都会从缓存清除。 ## 查询执行器 在这一阶段，我们有了经过优化的执行计划。这个计划会被编译成可执行代码。然后，如果有足够的资源（内存、CPU），查询执行器就会执行这个计划。计划中的运算符（JOIN, SORT BY …）可以顺序或并发执行，这取决于执行器。为了获取和写入数据，查询执行器与数据管理器进行交互，下一章我们就将介绍数据管理器。