## 数据结构 数据结构具体指同一类数据元素中，各元素之间的相互关系，包括三个组成成分，**数据的逻辑结构**，**数据的存储结构**和**数据运算结构**。 ### 数据(Data) - 数据是客观事物的符号表示，在计算机科学中指的是所有能输入到计算机中并被计算机程序处理的符号的总称。 - 数据元素(Data Element) :是数据的基本单位，在程序中通常作为一个整体来进行考虑和处理。一个数据元素可由若干个数据项(Data Item)组成。 - 数据项(Data Item) : 是数据的不可分割的最小单位。数据项是对客观事物某一方面特性的数据描述。 - 数据对象(Data Object) :是性质相同的数据元素的集合，是数据的一个子集。如字符集合C={‘A’,’B’,’C,…} 。 - 数据结构 :相互之间具有一定联系的数据元素的集合。 - 数据的逻辑结构 : 数据元素之间的相互关系称为逻辑结构。 - 数据操作 : 对数据要进行的运算 - 数据类型(Data Type):指的是一个值的集合和定义在该值集上的一组操作的总称。 ### 数据的逻辑结构 - 集合：结构中数据元素之间除了“属于同一个集合"外,再也没有其他的关系 - 线性结构：结构中的数据元素存在一对一的关系 - 树形结构：结构中的数据元素存在一对多的关系 - 网状或者图状结构：结构中的数据元素存在多对多的关系 ### 数据的存储结构 由数据元素之间的关系在计算机中有两种不同的表示方法——顺序表示和非顺序表示，从则导出两种储存方式，顺序储存结构和链式储存结构 - 顺序存储结构：用数据元素在存储器中的相对位置来表示数据元素之间的逻辑结构(关系)，数据元素存放的地址是连续的 - 链式存储结构：在每一个数据元素中增加一个存放另一个元素地址的指针(pointer)，用该指针来表示数据元素之间的逻辑结构(关系)，数据元素存放的地址是否连续没有要求 - 索引存储方法：除建立存储结点信息外，还建立附加的索引表来标识结点的地址 数据的逻辑结构和物理结构是密不可分的两个方面，一个算法的设计取决于所选定的逻辑结构，而算法的实现依赖于所采用的存储结构 ## 常见数据结构 ### 数组 > 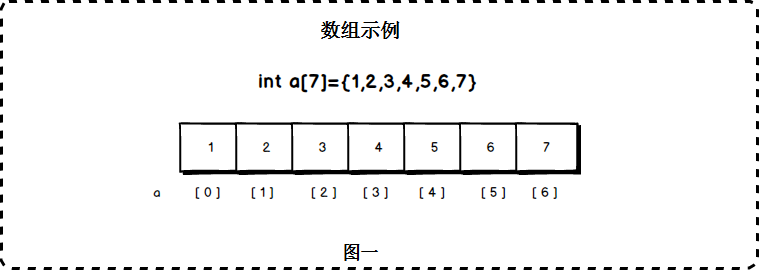把具有相同类型的若干变量按有序的形式组织起来。这些按序排列的同类数据元素的集合称为数组 两个特点：相同类型、有序 这个数组不等于PHP的数组。PHP数组本质是一个哈希表。通过数组实现  ### 链表 链表是一种物理存储单元上非连续、非顺序的存储结构 ，由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。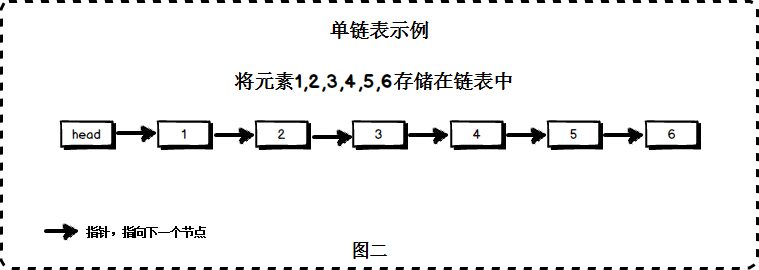 PHP SPL标准库中有SplDoublyLinkedList （双向链表）  链表的操作：插入、遍历、查找、删除 ```php $dlist=new SplDoublyLinkedList(); $dlist->push(1);//追加到末端 $dlist->add(1,3);//在index=1添加 //遍历 for($dlist->rewind();$dlist->valid();$dlist->next()){ echo $dlist->current()."<br/>"; } ``` ### 栈 > 是只能在某一端插入和删除的特殊[**线性表**]。它按照**先进后出**的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据（最后一个数据被第一个读出来）。 PHP中SPL标准库中有对应的实现 [SplStack ](http://php.net/manual/zh/class.splstack.php) 栈的两个操作 出栈pop、入栈push ```php $q = new SplStack(); $q[] = 1; $q[] = 2; $q[] = 3; $q->push(4); $q->push(5); echo $q->pop();//5 ``` ### 队列 > 一种特殊的[线性表]，它只允许在表的[前端]（front）进行删除操作，而在表的末端（rear）进行插入操作。进行插入操作的端称为队尾，进行删除操作的端称为队头。队列是按照“先进先出”或“后进后出”FIFO的原则组织数据的。队列中没有元素时，称为空队列。 PHP SPL标准库中有[SplQueue ](http://php.net/manual/zh/class.splqueue.php) 队列的两个操作 入队列enqueue、出队列dequeue ```php $q = new SplQueue(); $q->enqueue(array("FooBar", "foo")); $q->enqueue(array("FooBar", "bar")); $q->enqueue(array("FooBar", "msg", "Hi there!")); $f = $q->dequeue(); ``` ### 树 它是由n（n>=1）个有限节点组成一个具有层次关系的[集合]。是一对多的关系。 （1）有且仅有一个结点 K0，他对于关系N来说没有前驱，称K0为树的根结点。简称为根（root)）。　 （2）除K0外，K中的每个结点，对于关系N来说有且仅有一个前驱。 （3）K中各结点，对关系N来说可以有m个后继（m>=0）。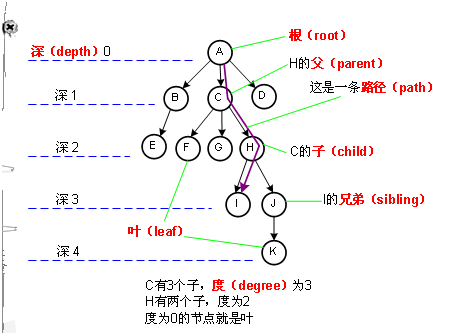  #### 1. 二叉树 除了叶以外的结点，都有两个子。（叶就是在它和根的路径上，没有比他更远的结点了，也可以理解为，只有一个结点和它相连，并且它不是根，那么他就是叶） #### 2. 二叉搜索树 二叉搜索树，也称有序二叉树,排序二叉树，是指一棵空树或者具有下列性质的二叉树： 1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 3. 任意节点的左、右子树也分别为二叉查找树。 4. 没有键值相等的节点。 #### 3. 树的遍历 - 先序遍历 访问根结点——》访问左子树——》访问右子树 - 中序遍历 先访问左子树，再访问根，再访问右子树。 - 后序遍历 访问根结点——》访问右子树——》访问左子树 ### 堆 堆是一种特殊的树形数据结构，每个结点都有一个值。通常我们所说的堆的数据结构，是指二叉堆。堆的特点是根结点的值最小（或最大），且根结点的两个子树也是一个堆。 比如我们查找top N 就可以用堆  PHP中有堆的实现SplMaxHeap (大端堆)、SplMaxHeap （小端堆） ### 散列表【HashTable】 K=>V结构。若结构中存在关键字和K相等的记录，则必定在f(K)的存储位置上。由此，不需比较便可直接取得所查记录。称这个对应关系f为散列函数(Hash function)，按这个思想建立的表为[散列表]。 #### 冲突 若 key1 ≠ key2 ，而 f(key1) = f(key2)，这种情况称为**冲突**(Collision)。 #### 构造哈希函数 常见的构造哈希表的方法有 5 种： **（1）直接定址法** 说白了，就是小学时学过的**一元一次方程**。 即 f(key) = a * key + b。其中，a和b 是常数。 **（2）数字分析法** 假设关键字是R进制数（如十进制）。并且哈希表中**可能出现的关键字都是事先知道的**，则可选取关键字的若干数位组成哈希地址。 选取的原则是使得到的哈希地址尽量避免冲突，即所选数位上的数字尽可能是随机的。 **（3）平方取中法** 取关键字平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况，仅取其中的几位为地址不一定合适； 而一个数平方后的中间几位数和数的每一位都相关， 由此得到的哈希地址随机性更大。取的位数由表长决定。 **（4）除留余数法** 取关键字被某个**不大于哈希表表长** m 的数 p 除后所得的余数为哈希地址。 即 f(key) = key % p (p ≤ m) 这是一种**最简单、最常用**的方法，它不仅可以对关键字直接取模，也可在折叠、平方取中等运算之后取模。 注意：p的选择很重要，如果选的不好，容易产生冲突。根据经验，**一般情况下可以选p为素数**。 ### 冲突解决 **1）开放定址法** 如果两个数据元素的哈希值相同，则在哈希表中为后插入的数据元素另外选择一个表项。 当程序查找哈希表时，如果没有在第一个对应的哈希表项中找到符合查找要求的数据元素，程序就会继续往后查找，直到找到一个符合查找要求的数据元素，或者遇到一个空的表项 **2）拉链法** 将哈希值相同的数据元素存放在一个链表中，在查找哈希表的过程中，当查找到这个链表时，必须采用线性查找方法。在这种方法中，哈希表中每个单元存放的不再是记录本身，而是相应同义词单链表的头指针。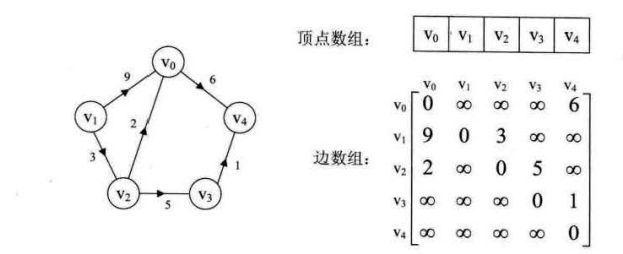 ### 图 图是由结点的有穷集合V和边的集合E组成。其中，为了与树形结构加以[区别]，在图结构中常常将结点称为顶点，边是顶点的有序偶对，若两个顶点之间存在一条边，就表示这两个顶点具有相邻关系。  学习资料: - [https://visualgo.net/en](https://visualgo.net/en) - [http://www.cnblogs.com/jingmoxukong/p/4329079.html](http://www.cnblogs.com/jingmoxukong/p/4329079.html) - [https://www.studytonight.com/data-structures/introduction-to-data-structures](https://www.studytonight.com/data-structures/introduction-to-data-structures) - [https://www.tutorialspoint.com/data_structures_algorithms/index.htm](https://www.tutorialspoint.com/data_structures_algorithms/index.htm)