# 使用orange进行聚类分析 小麦籽粒几何性状的测定 ## 知识点 - 数据的预处理 - Orange 数据集的格式 - 数据分布的含义 - 特征排序 - ## 实验过程 ### 数据集 种子数据集：https://archive.ics.uci.edu/ml/datasets/seeds > 以下链接下载的文件是一个txt文件，使用TAB格式分隔的，数据需要简单的处理以下才能正常使用。 https://archive.ics.uci.edu/ml/machine-learning-databases/00236/seeds_dataset.txt 处理完的实验数据集，在课程资源包中提供，并做了汉化。     三种不同品种小麦籽粒几何性状的测定。用于软X射线技术和GRAINS构建七个实值属性，所有这些参数都是实值连续的。     1、面积A，      2、周长P，      3、紧凑度C = 4 * pi * A / P ^ 2,4      4、籽粒长度，      5、籽粒宽度，      6、不对称系数      7、核槽的长度。      下载数据的文件格式为.txt格式，将文件格式改为.csv或.xlsx格式。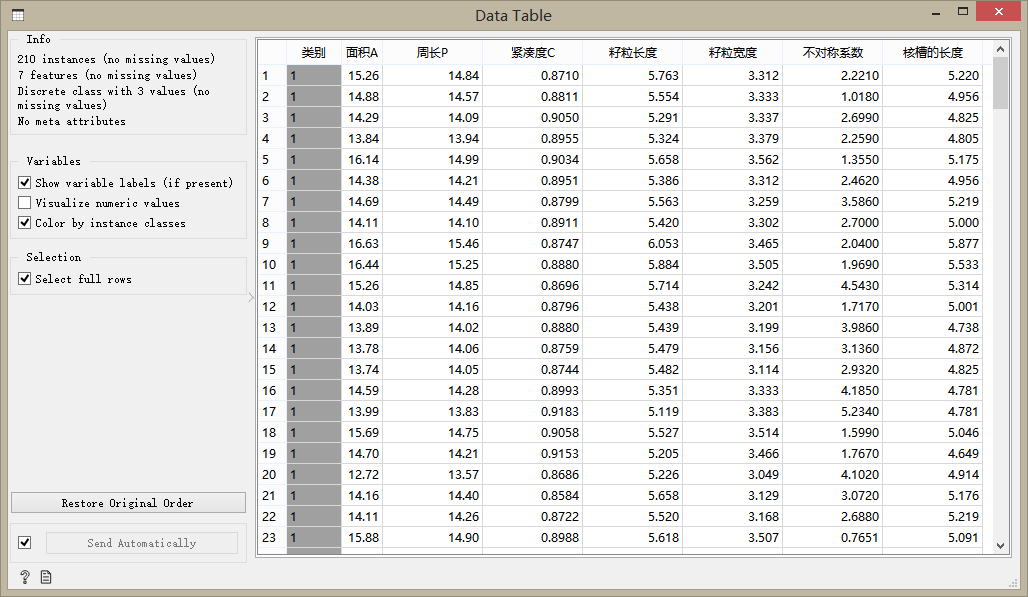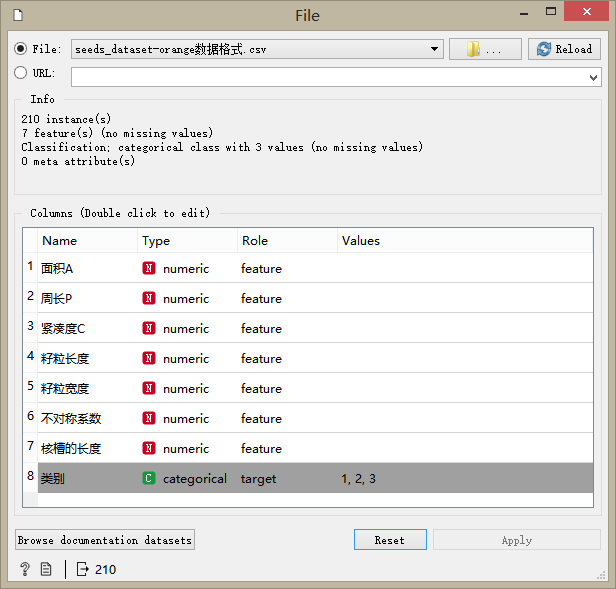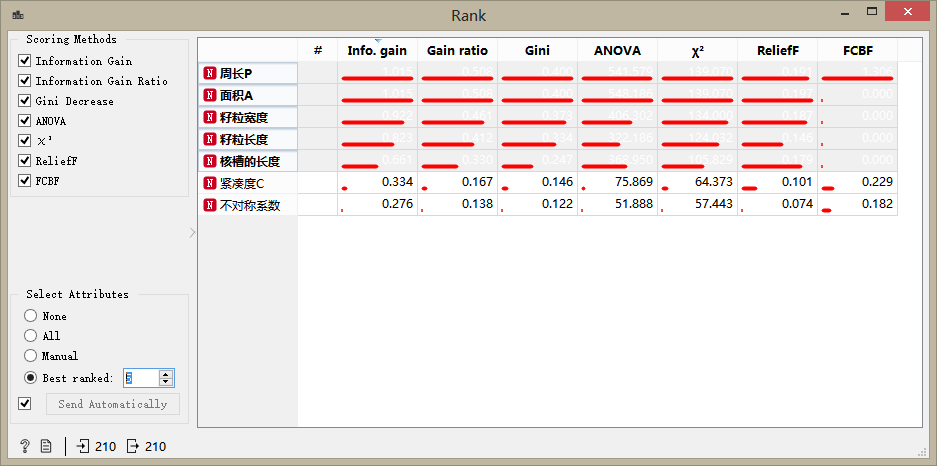 使用Data Table组件查看数据，显示的一部分数据  ### 数据预处理 打开orange软件，进行数据预处理  加入文件（File）组件，设置数据源（File）为前面下载并处理后的数据集，设置类别的角色（Role）为目标（target），并将其类型（Type）改成目录化（Categorical）  特征排序组件（Rank）可以根据数据特征的相关性对其进行排名和筛选，我们只关心那些对分类有较大帮助的特征（信息量比较大的），双击控件：  可以看出，紧凑度（compactness）和不对称性（asymmetry）特征的信息量值很低，故将其筛除。 > 可以用数据分布组件（Distributions）通过观察紧凑度（compactness）和不对称性（asymmetry）特征值的分布进行验证。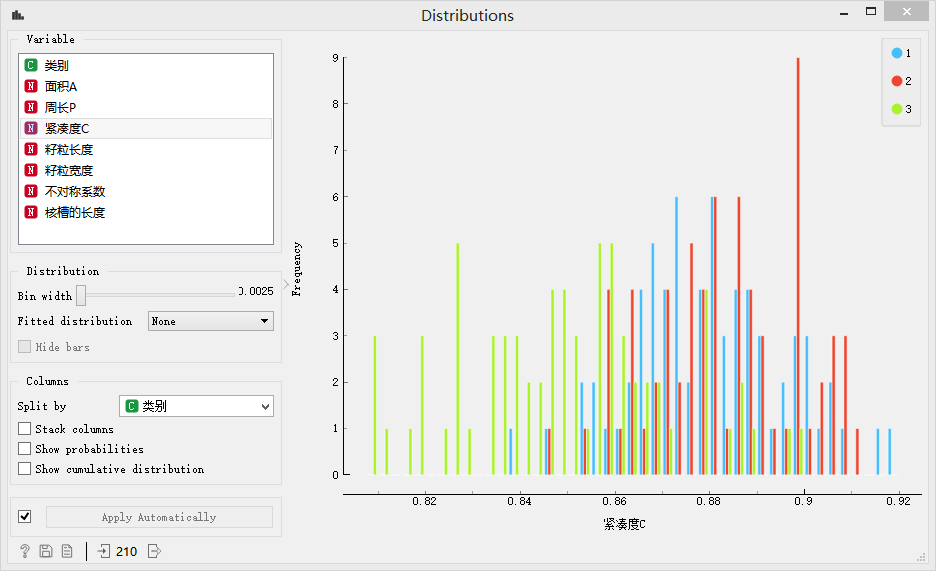 紧凑度的统计分布  > 分布图中可以看出3种类别的数据都混合在一起，因此该特征很难区分不同的类别的种子，因此不合适作为分类的特征，或者说该特征对分类任务来说提供的信息量是很少的。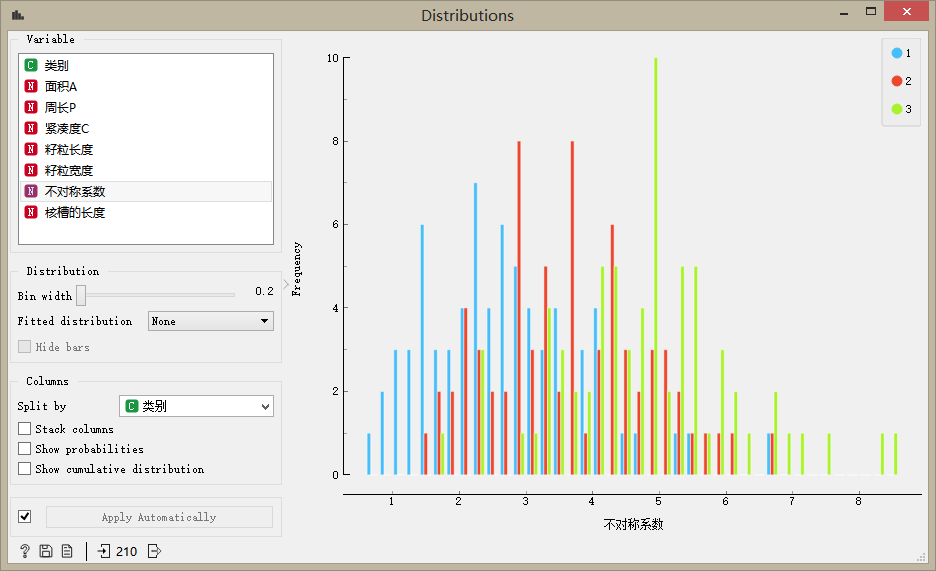 不对称系统的统计分布  ## 聚类 ### K-means算法 k均值聚类算法（k-means clustering algorithm）是一种迭代求解的算法，其步骤是： 预将数据分为K组，则随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。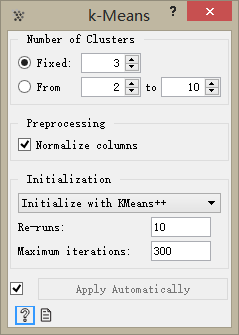 双击K-means控件，设置算法参数： > 输入固定簇数（Number of Clusters）：3  > 选择使用K-means++算法进行初始化 ### 层次聚类 先用距离组件（Distances）计算成对距离的矩阵，然后用层次聚类组件（Hierarchical Clustering）显示从输入距离矩阵构造的层次聚类的树形图        选择Top N = 3,传入数据流到Scatter Plot控件进行可视化： 结果分析：        用Silhouette Plot轮廓组件评价聚类效果。数据越靠近数据簇中心，轮廓值越大；离簇中心越远，轮廓值越小：0为位于两簇之间的点，负数为错误划分到别的簇中。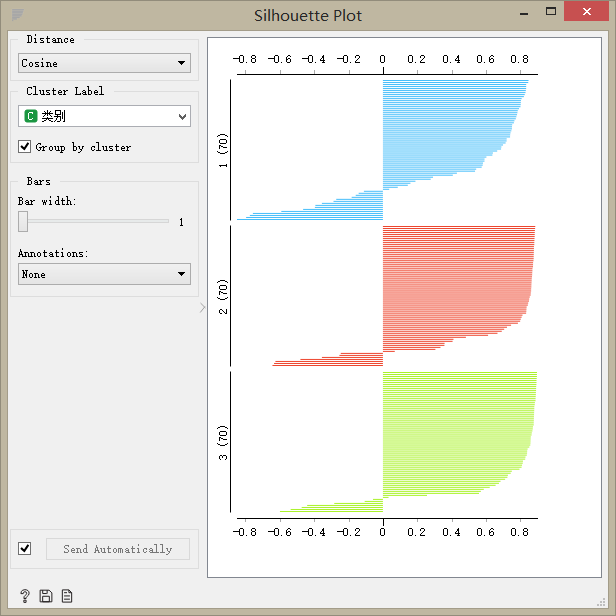 K-means轮廓图：  K-means++轮廓图 层次轮廓图：        通过对比其轮廓图，我们发现：在对该数据进行聚类时，K-means算法要比层次聚类要好，层次聚类中有出现负值；而k-means++算法将数据聚成两簇，没有达到我预期得到的聚类结果。