[TOC] ## 启动时长统计 ### TraceView和SysTrace工具 ### 手工打点 ActionS: 进程不存在的情况下，点击icon启动执行到SplashActivity#onDrawComplete的耗时 ActionR: 进程不存在的情况下，点击icon启动执行到SplashActivity#onDrawComplete后，到消息同步完毕的耗时 ### 无痕迹打点 ASM编译插桩 ## 启动优化手段 ### 显示优化 #### 1.将启动页主题背景设置成闪屏页图片 这么做的目的主要是为了消除启动时的黑白屏，给用户一种秒响应的感觉，但是并不会真正减少用户启动时间，仅属于视觉优化。 #### 2.主页面布局优化 1）通过减少冗余或者嵌套布局来降低视图层次结构 2）用 ViewStub 替代在启动过程中不需要显示的 UI 控件 ## 黑科技优化 ### redex 重排列 class 文件 通过文件重排列的目的，就是将启动阶段需要用到的文件在 APK 文件中排布在一起，尽可能的利用 Linux 文件系统的 pagecache 机制，用最少的磁盘 IO 次数，读取尽可能多的启动阶段需要的文件，减少 IO 开销，从而达到提升启动性能的目的。 ### 在类加载的过程中通过 Hook 去掉类验证的过程 ### 低端机，MultipDex #### ClassLoader 加载类原理： > ClassLoader.loadClass -> DexPathList.loadClass -> 遍历dexElements数组 ->DexFile.loadClassBinaryName 通俗点说就是：ClassLoader加载类的时候是通过遍历dex数组，从dex文件里面去加载一个类，加载成功就返回，加载失败则抛出Class Not Found 异常。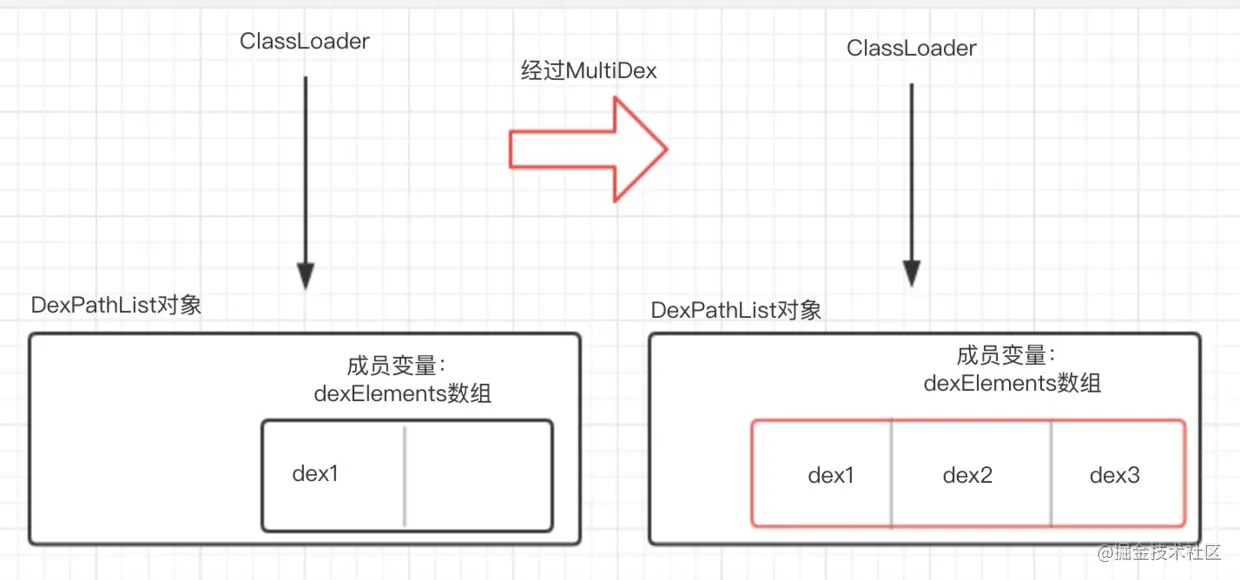 #### MultiDex原理： > 在明白ClassLoader加载类原理之后，我们可以通过反射dexElements数组，将新增的dex添加到数组后面，这样就保证ClassLoader加载类的时候可以从新增的dex中加载到目标类，经过分析后最终MultipDex原理图如下： >  #### MultiDex优化 install过程为什么耗时，因为涉及到解压apk取出dex、压缩dex、将dex文件通过反射转换成DexFile对象、反射替换数组。 1. 在Application 的attachBaseContext 方法里，启动另一个进程的LoadDexActivity去异步执行MultiDex逻辑，显示Loading。 2. 然后主进程Application进入while循环，不断检测MultiDex操作是否完成 3. MultiDex执行完之后主进程Application继续走，ContentProvider初始化和Application onCreate方法，也就是执行主进程正常的逻辑。 ## 业务优化 ### 减少启动过程中的 GC 优化/IO读取 ### 第三方库懒加载 很多第三方开源库都说在Application中进行初始化，十几个开源库都放在Application中，肯定对冷启动会有影响，所以可以考虑按需初始化，例如Glide，可以放在自己封装的图片加载类中，调用到再初始化，其它库也是同理，让Application变得更轻。 ### 线程优化 线程是程序运行的基本单位，线程的频繁创建是耗性能的，所以大家应该都会用线程池。单个cpu情况下，即使是开多个线程，同时也只有一个线程可以工作，所以线程池的大小要根据cpu个数来确定。 ## 异步加载 异步加载。将耗时任务放到子线程加载，等到所有加载任务加载完成之后，再进入首页。 多线程异步加载方案确实是 ok 的。但如果遇到前后依赖的关系呢。比如任务2 依赖于任务 1，这时候要怎么解决呢。 有向无环图。它可以完美解决先后依赖关系。 ### 有向无环图 **有向无环图**（Directed Acyclic Graph, DAG）是有向图的一种，字面意思的理解就是图中没有环。常常被用来表示事件之间的驱动依赖关系，管理任务之间的调度。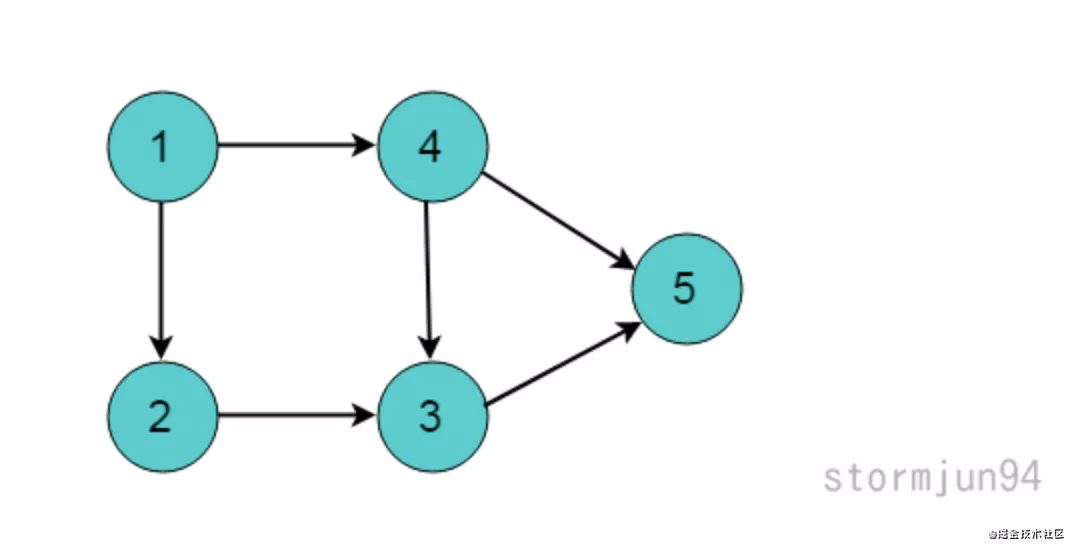  **顶点**：图中的一个点，比如顶点 1，顶点 2。 **边**：连接两个顶点的线段叫做边，edge。 **入度**：代表当前有多少边指向它。 在上图中，顶掉 1 的入度是 0，因为没有任何边指向它。顶掉 2 的入度是 1， 因为 顶掉 1 指向 顶掉 2. 同理可得出 5 的入度是 2，因为顶掉 4 和顶点 3 指向它。 **拓扑排序**：拓扑排序是对一个有向图构造拓扑序列的过程。它具有如下特点。 * 每个顶点出现且只出现一次。 * 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面 由于有这个特点，因此常常用有向无环图的数据结构用来解决依赖关系。 上图中，拓扑排序之后，任务2肯定排在任务1之后，因为任务2依赖 任务1， 任务3肯定在任务2之后，因为任务3依赖任务2。 拓扑排序一般有两种算法，第一种是入度表法，第二种是 DFS 方法。下面，让我们一起来看一下怎么实现它。 ### 入度表法 入度表法是根据顶点的入度来判断是否有依赖关系的。若顶点的入度不为 0，则表示它有前置依赖。它也常常被称作**BFS 算法**。 #### 算法思想 * 建立入度表，入度为 0 的节点先入队。 * 当队列不为空，进行循环判断。 * 节点出队，添加到结果 list 当中。 * 将该节点的邻居入度减 1。 * 若邻居节点入度为 0，加入队列。 * 若结果 list 与所有节点数量相等，则证明不存在环。否则，存在环。