数据结构大致包含以下几种存储结构： **线性表**：零个或多个数据元素的有限序列 还可细分为顺序表（底层实现靠数组）、链表、栈和队列；栈和队列隶属于线性表，是特殊的线性表。 元素有多个时，第一个元素无前驱，最后一个无后继，其他每个元素都有且只有一个前驱和后继。 **树结构**：包括普通树，二叉树，线索二叉树等； **图存储结构** ## 数组、顺序表（顺序存储结构） 顺序存储：一段地址连续的存储单元依次存储线性表的数据元素。 三个重要属性： **起始位置、最大存储容量、当前长度** 查询的时间复杂度 o（1） 插入和删除的复杂度是o（n）。   插入时，后面的数据都要往后移动，删除时，后面的数据都要往前移动 **优点：** 可以快速的存取表中任一位置的元素。 不需要为表示元素之间的逻辑关系而增加额外存储空间。 **缺点：** 插入和删除操作需要移动大量元素、性能受损 当元素数量变化较大，难以确定最大存储容量 造成存储空间的“碎片” 顺序表底层就是使用数组。 ## 链表、链式存储结构 链式存储：地址可以连续也可以不连续的存储单元存储数据元素 数据域：存储数据元素信息的域 指针域：存储直接后继位置的域（后一个元素的地址） 数据域 + 指针域  就是结点 ### 单链表 单链表：链表中的每个结点中只包含一个指针域 头指针：链表中第一个结点的存储位置 头结点：有时会为了方便，会在单链表的第一个结点前附设一个节点，就是头结点，头结点的数据域可以不存储任何信息。 头指针和头结点的区别： 头指针是指链表指向第一个结点的指针，若链表有头结点，则是指向头结点的指针 头指针具有标识作用，所以常用头指针冠以链表的名字 无论链表是否为空，头指针均不为空。头指针是链表的必要元素 头结点是为了操作的统一和方便而设立的，放在第一个元素的结点之前，其数据域一般无意义。 有了头结点，对在第一个元素节点前插入结点和删除第一个结点，其操作与其他结点的操作就统一了。 头结点不一定是链表必须要素 查询的时间复杂度 o（1）到o（n） ，查第一个就是o（1），最坏的情况是 o（n） 插入和删除的复杂度，当知道元素的指针位置时是o（1），否则需要先查询，复杂度则变成o（n）。   插入和删除越频繁的操作，单链表的效率优势就越是明显。 工作指针后移 ## 顺序存储结构和单链表存储结构的区别 * 存储分配方式： * 顺序存储结构用一段连续的存储单元依次存储线性表的数据元素。 * 单链表采用链式存储结构，用一组任意的存储单元存放线性表的元素。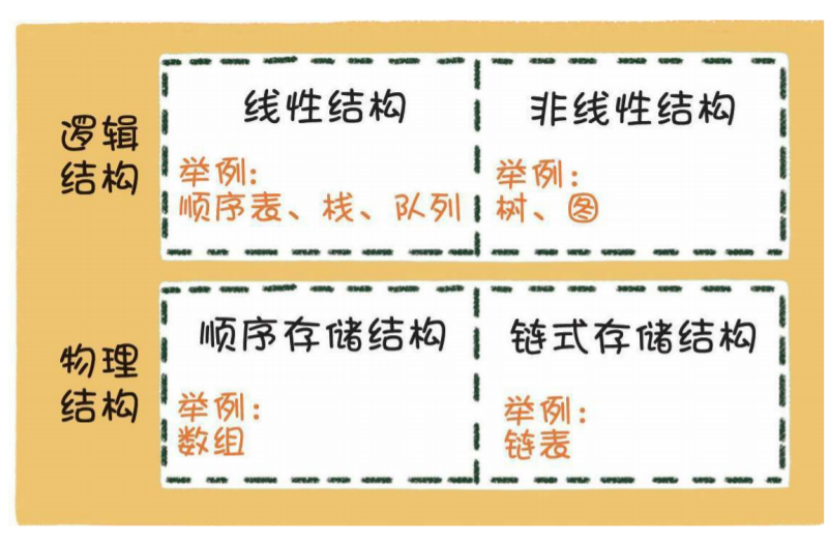 * 时间性能： * 查找： * 顺序存储结构O(1) * 单链表O(n) * 插入和删除 * 顺序存储结构需要平均移动表长一半的元素，时间为O(n) * 单链表在线出某位置的指针后，插入和删除时间仅为O(1) * 空间性能 * 顺序存储需要预分配存储空间，分大了浪费，分小了易发生上溢 * 单链表不需要分配存储空间，只要有就可以分配，元素个数也不受限制 结论： **插入和删除频繁的使用单链表结构，频繁查找的使用顺序存储结构** **元素个数变化较大或根本无法确定可能的个数范围，最好考虑单链表，这样不需要考虑存储空间的大小** ## 逻辑结构和物理结构  ## 栈 栈是限定仅在表尾进行插入和删除操作的线性表。 我们把允许**插入和删除的一端称为栈顶**(top)，**另一端称为栈底**(bottom)，不含任何数据元素的栈称为空栈。栈又称为后进先出(Last In First Out)的线性表，简称LIFO结构。 栈元素也具有线性关系，栈是一种特殊的线性表。定义中说是在线性表的表尾插入和删除操作，这里表尾是指栈顶，而不是栈底。特殊在于限制了这个线性表的插入和删除位置，只在栈顶进行。 栈的插入操作，叫作进栈，也称压栈、入栈。类似子弹入弹夹。 栈的删除操作,叫作出栈,也有的叫作弹栈。如同弹夹中的子弹出夹。 ## 队列 队列是只允许在一端进行插入操作、而在另一端进行删除操作的线性表。 队列是一种先进先出(First In First Out)的线性表,简称FIFO,允许插入的一端称为队尾，允许删除的一端称为队头。 同样是线性表，队列也有类似线性表的各种操作，不同的就是插入数据只能在队，尾进行，删除数据只能在队头进行。 把队列的这种头尾相接的顺序存储结构称为循环队列。队尾指针指向的位置永远空出1位，所以队列 最大容量比数组长度小1。 队列的链式存储结构，其实就是线性表的单链表，只不过它只能尾进头出而已，我们把它简称为链队列。 **双端队列:** 这种数据结构，可以说综合了栈和队列的优点，对双端队列来说，从队头一端可以入队或出队，从队尾一端也可以入队或出队。尽管双端队列看起来似乎比栈和队列更灵活，**但实际上在应用程序中远不及栈和队列有用。** **优先队列**:  优先队列已经不属于线性数据结构的范畴了，它是基于二叉堆来实现 ## hash 哈希 (散列表) 散列表也叫作哈希表 （hash table），这种数据结构提供了键（Key）和值（Value） 的映射关系。 底层使用数组, 通过哈希函数将 key 转为 数组下标 当数据量大时， 容易出现哈希函数将不同的key 转为数组下标时出现相同的值， 这就是**哈希冲突** 哈希冲突的解决： 开放寻址法：如果经过哈希函数获得的下标所在位置已经有值，则往后移动一位，如果移动到的位置也已经有值了，就继续往后移动，直到找到空位。开放寻址法有多种，这是最简单的，java 的 ThreadLocal 就是这样做的。 链表法（拉链法）：如果经过哈希函数获得的下标所在位置已经有值，则在这个位置增加一个链表，这个位置所有的数据以key value 的对象形式都放到链表里，相当于数组嵌套链表。java的HashMap是这样做的（1.8以后应该是红黑树） ### hash 的扩容 对于JDK中的散列表实现类HashMap来说，影响其扩容的因素有两个。 Capacity ，即HashMap的当前长度 LoadFactor ，即HashMap的负载因子，默认值为0.75f HashMap.Size >= Capacity×LoadFactor **hash 扩容过程** 扩容 ，创建一个新的Entry空数组，长度是原数组的2倍。 重新Hash ，遍历原Entry数组，把所有的Entry重新Hash到新数组中。为什么要重新Hash呢？因为长度扩大以后，Hash的规则也随之改变。 经过扩容，原本拥挤的散列表重新变得稀疏，原有的Entry也重新得到了尽可能均匀的分配。 ## 树 树（tree）是n（n≥0）个节点的有限集。当n=0时，称为空树。在任意一 个非空树中。 主要特点： 有且仅有一个特定的称为根的节点。 当n>1时，其余节点可分为m（m>0）个互不相交的有限集，每一个集 合本身又是一个树，并称为根的子树。 没 有“孩子”的节点是叶子节点 树的最大层级数，被称为树的高度或深度 ### 二叉树 这种树 的每个节点**最多有2个**孩子节点，也可能只 有1个，或者没有孩子节点。 二叉树节点的两个孩子节点，一个被称为左孩子（left child） ，一个被 称为右孩子（right child） 。 二叉树还有两种特殊形式，一个叫作满二叉树 ，另一个叫作完 全二叉树 。 **满二叉树：**一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在 同一层级上，那么这个树就是满二叉树。 满二叉树要求所有分支都是 满的；而**完全二叉树**只需保证**最后一个节点之前的节点都齐全**即可。 二叉树可以用哪些物理存储结构来表达呢？ 1. 链式存储结构。 2. 数组。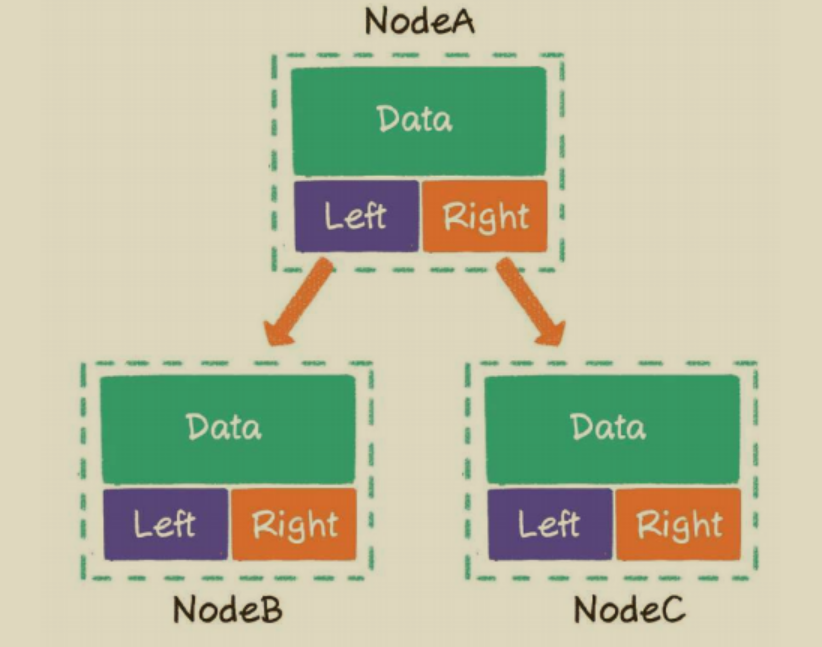  链表：一个节点最多可以指向左右两个孩子节点，所 以二叉树的每一个节点包含3部分。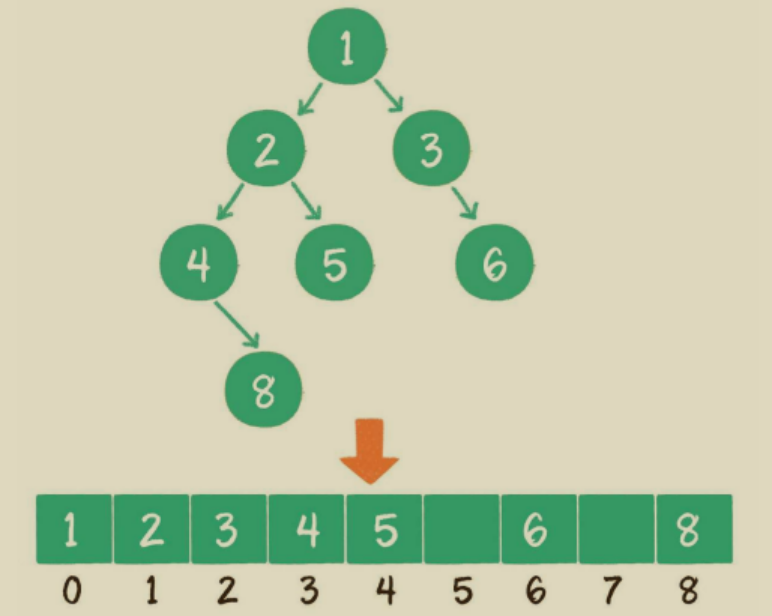 存储数据的data变量 指向左孩子的left指针 指向右孩子的right指针  数组：按照层级顺序把二叉树的节点放到数组中对应的位 置上。如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空 出来 假设一个父节点的下标是parent，那么它的左孩子节点下标就 是2×parent + 1 ；右孩子节点下标就是2×parent + 2 。 反过来，假设一个左孩子节点的下标是leftChild，那么它的父节点下标 就是（leftChild-1）/ 2 。 ### 二叉查找树（二叉排序树） 二叉查找树在二叉树的基础上增加了以下几个条件。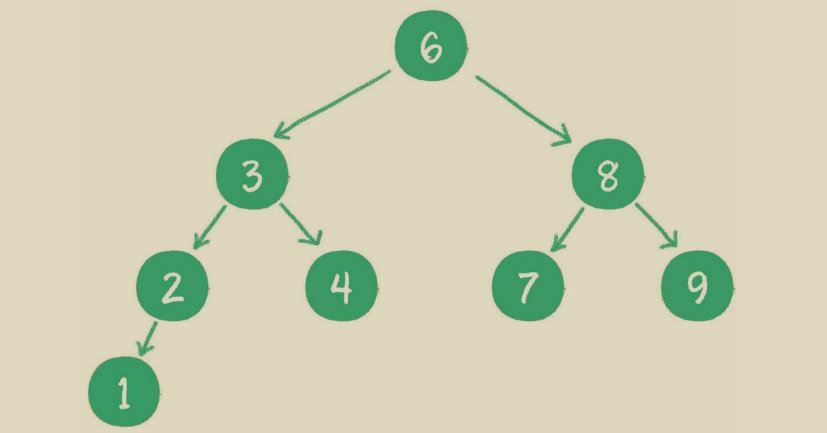 * 如果左子树不为空，则左子树上所有节点的值均小于根节点的值 * 如果右子树不为空，则右子树上所有节点的值均大于根节点的值 * 左、右子树也都是二叉查找树  二叉查找树 利于查找和排序，但 9 8 7 6 5 等节点树时会涉及二叉树的自平衡，二叉树自平衡的 方式有多种，如红黑树、AVL树、树堆等。 二叉树的遍历 1\. 深度优先遍历 （前序遍历、中序遍历、后序遍历）。 2\. 广度优先遍历 （层序遍历）。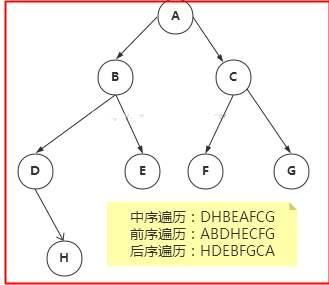 深度优先遍历 二叉树前序遍历、中序遍历、后序遍历、层序遍历的直观理解 [https://blog.csdn.net/u013834525/article/details/80421684](https://blog.csdn.net/u013834525/article/details/80421684) （前序遍历、中序遍历、后序遍历） 指的是 输出根节点的顺序  二叉树的前序遍历，输出顺序是根节点、左子树、右子树。 输出顺序 根 =》左 =》右 1\. 从树的根节点开始输出根节点，然后一直遍历并输出左子树的左节点，直到节点没有左子树为止，这时候再去遍历最后一个左节点的右子树或者父节点的右子树 2\. 遍历右子树时， 有左子树的，再按照1的流程遍历输出这个右子树。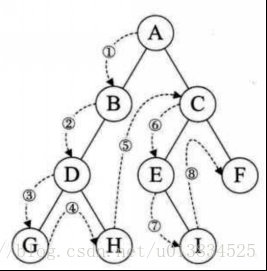  二叉树的中序遍历，输出顺序是左子树、根节点、右子树。 输出顺序 左 =》根 =》右 1\. 首先访问根节点的左孩子，如果这个左孩子还拥有左孩子，则继续深 入访问下去，一直找到不再有左孩子的节点，并输出该节点。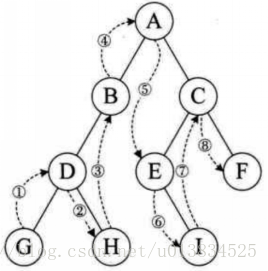  二叉树的后序遍历，输出顺序是根节点、左子树、右子树。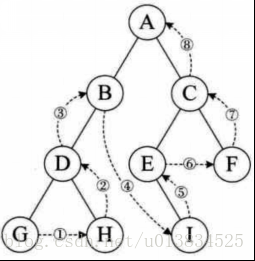 输出顺序 左 =》右 =》根  广度优先遍历 层序遍历，顾名思义，就是二叉树按照从根节点到叶子节点的层次关 系，一层一层横向遍历各个节点。代码实现可以使用队列  二叉堆 二叉堆本质上是一种完全二叉树，它分为两个类型。 1\. 最大堆。 最大堆的任何一个父节点的值，都大于或等于 它 左、右孩子节点的值。 2\. 最小堆。 最小堆的任何一个父节点的值，都小于或等于它左、 右孩子节点的值。 二叉堆的根节点叫作堆顶 。 最大堆的堆顶是整个堆中的最大元素 ；最小堆的堆顶是整个堆中的最小元素 。 堆的删除操作是单一节点的“下沉”，这两个操作的平均交换 次数都是堆高度的一半，所以时间复杂度是O(logn)。至于堆的构 建，需要所有非叶子节点依次“下沉”，所以我觉得时间复杂度应该 是O(n) 二叉堆虽然是一个完全二叉 树，但它的存储方式并不是链式存储，而是顺序存储。换句话说，二叉 堆的所有节点都存储在数组中。 假设父节点的下标是parent，那么它的左孩子下标就是 2×parent+1 ；右 孩子下标就是2×parent+2 。