# 数据结构与算法
## 1. 什么是数据结构
~~~
官方解释:
数据结构是一门研究非数值计算的程序设计问题中的操作对象,以及他们之间的关系和操作等相关问题的学科。
大白话:
数据结构就是把数据元素按照一定的关系组织起来的集合,用来组织和存储数据
~~~
## 2. 数据结构分类
**传统上,我们可以把数据结构分为逻辑结构和物理结构两大类。**
### 2.1逻辑结构分类:
逻辑结构是从具体问题中抽象出来的模型,是抽象意义上的结构,按照对象中数据元素之间的相互关系分类,也是
我们后面课题中需要关注和讨论的问题。
**a.集合结构:集合结构中数据元素除了属于同一个集合外,他们之间没有任何其他的关系。**
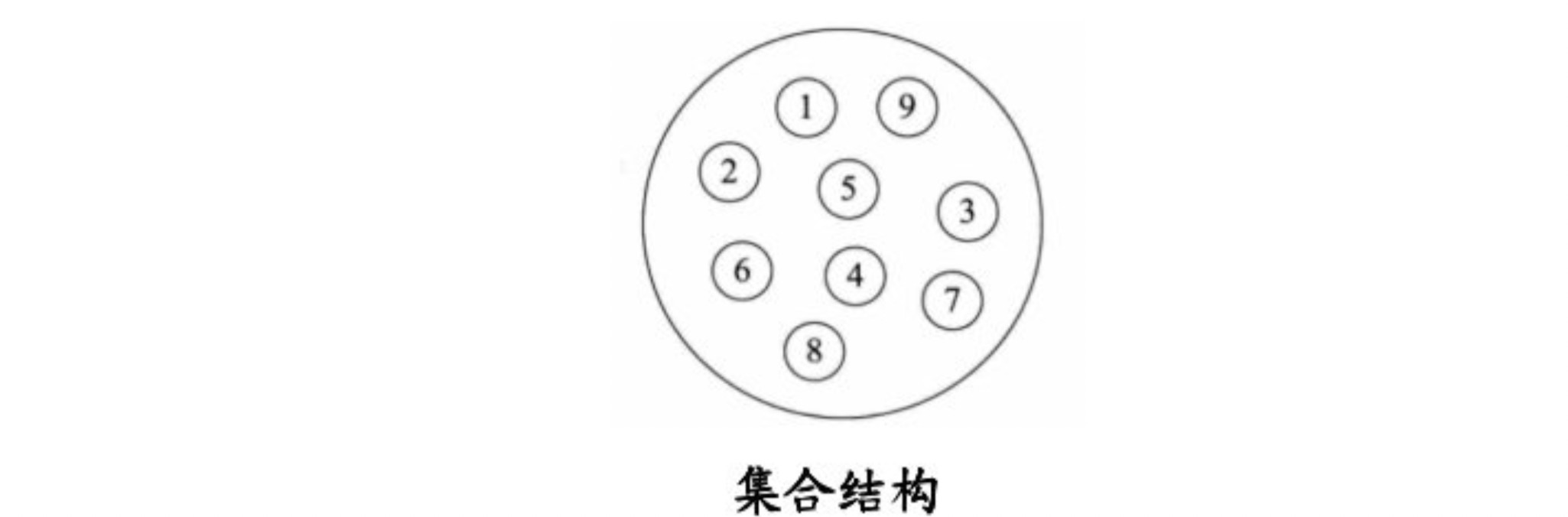
**b.线性结构:线性结构中的数据元素之间存在一对一的关系**
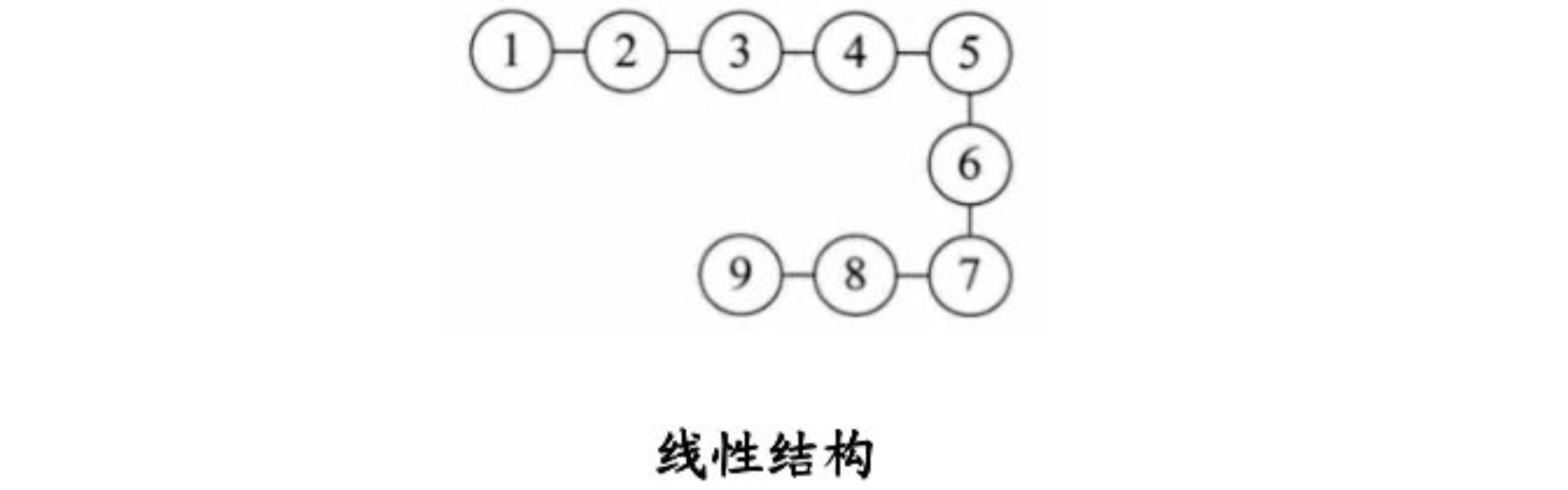
**c.树形结构:树形结构中的数据元素之间存在一对多的层次关系**
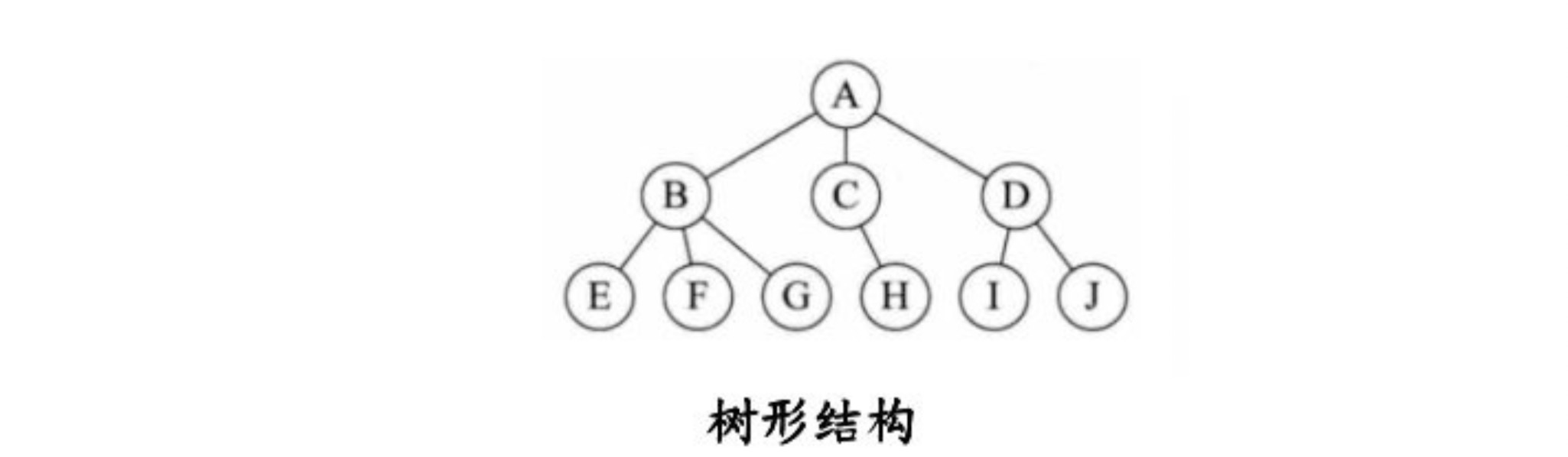
**d.图形结构:图形结构的数据元素是多对多的关系**
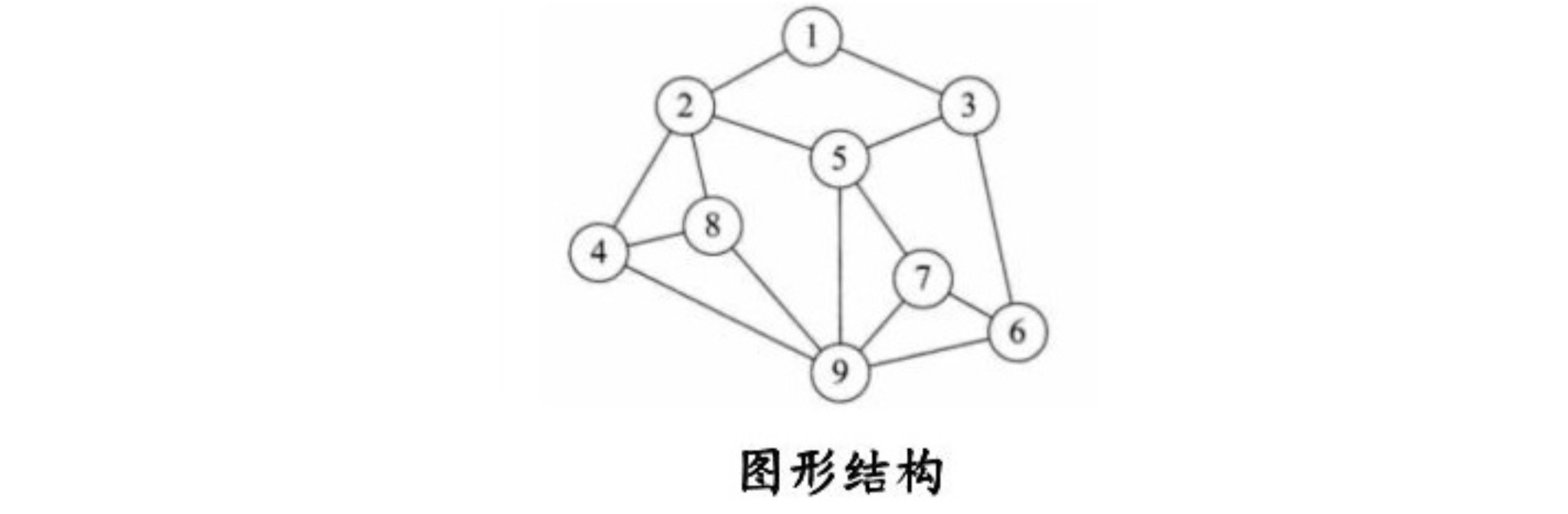
### 2.2物理结构分类:
逻辑结构在计算机中真正的表示方式(又称为映像)称为物理结构,也可以叫做存储结构。常见的物理结构有顺序
存储结构、链式存储结构。
**顺序存储结构:**
把数据元素放到地址连续的存储单元里面,其数据间的逻辑关系和物理关系是一致的 ,比如我们常用的数组就是 顺序存储结构。

**链式存储结构:**
顺序存储结构存在一定的弊端,就像生活中排时也会有人插队也可能有人有特殊情况突然离开,这时候整个结构都
处于变化中,此时就需要链式存储结构。
链式存储结构是把数据元素存放在任意的存储单元里面,这组存储单元可以是连续的也可以是不连续的。此时,数据元素之间并
不能反映元素间的逻辑关系,因此在链式存储结构中引进了一个指针存放数据元素的地址,这样通过地址就可以找
到相关联数据元素的位置
## 3. 什么是算法
**官方解释:**
算法是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法解决问题的策略
机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。
**大白话:**
根据一定的条件,对一些数据进行计算,得到需要的结果。
### 3.1算法初体验
在生活中,我们如果遇到某个问题,常常解决方案不是唯一的。
~~~
例如从西安到北京,如何去?会有不同的解决方案,我们可以坐飞机,可以坐火车,可以坐汽车,甚至可以步行,
不同的解决方案带来的时间成本和金钱成本是不一样的,比如坐飞机用的时间最少,但是费用最高,步行费用最
低,但时间最长。
~~~
~~~
再例如在北京二环内买一套四合院,如何付款?也会有不同的解决方案,可以一次性现金付清,也可以通过银行做 按揭。
这两种解决方案带来的成本也不一样,一次性付清,虽然当时出的钱多,压力大,但是没有利息,按揭虽然 当时出的钱少,
压力比较小,但是会有利息,而且30年的总利息几乎是贷款额度的一倍,需要多付钱。
~~~
在程序中,我们也可以用不同的算法解决相同的问题,而不同的算法的成本也是不相同的。总体上,一个优秀的算
法追求以下两个目标:
1. 花最少的时间完成需求;
2. 占用最少的内存空间完成需求;
### 3.2算法实践
**需求1:计算1到100的和**
解法1:
```
public function get100Sum(){
$sum=0;
$n=100;
for ($i=1; $i<$n ; $i++) {
$sum+=$i;
}
echo "1到100的和是:".$sum;
}
```
解法2:
```
public function getSum100(){
$sum=0;
$n=100;
$sum = ($n+1)*$n/2
echo "1到100的和是:".$sum;
}
```
第一种解法要完成需求,要完成以下几个动作: 1.定义两个整型变量;
2.执行100次加法运算;
3.打印结果到控制台;
第二种解法要完成需求,要完成以下几个动作:
1.定义两个整型变量; 2.执行1次加法运算,1次乘法运算,一次除法运算,总共3次运算; 3.打印结果到控制台;
很明显,第二种算法完成需求,花费的时间更少一些。
**需求2: 计算10的阶乘**
解法1:
```
static function fun1($n){
if($n==1){
return 1;
}
return $n*self::fun1($n-1);
}
```
解法2:
```
static function fun1($n){
$res=1;
for ($i=1; $i<=$n ; $i++) {
$res*=$i;
}
return $res;
}
```
第一种解法,使用递归完成需求,fun1方法会执行10次,并且第一次执行未完毕,调用第二次执行,第二次执行 未完毕,调用第三次执行...最终,最多的时候,需要在栈内存同时开辟10块内存分别执行10个fun1方法。
第二种解法,使用for循环完成需求,fun2方法只会执行一次,最终,只需要在栈内存开辟一块内存执行fun2方法 即可。
很明显,第二种算法完成需求,占用的内存空间更小。
## 4.总结
以上就是数据结构与算法的概述,我闷在实际开发中,使用不同的算法,不同的数据结构会对我们的查询速度产生很大的影响,后续会给大家介绍如何选择数据结构以及算法。
