# 算法时间复杂度
算法的时间复杂度就是指算法执行时间多少的意思。
而上一章我们分析了函数的线性增长已经得出了影响算法函数的有关因素
```
1.算法函数中的常数可以忽略;
2.算法函数中最高次幂的常数因子可以忽略;
3.算法函数中最高次幂越小,算法效率越高。
```
所以算法函数越简单的算法时间复杂度越低。而且我们有一个专业的大O记法来表示算法复杂度。
## **1.大O记法**
**定义:**
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随着n的变化情况并确定T(n)的 量级。算法的时间复杂度,就是算法的时间量度,记作:T(n)=O(f(n))。它表示随着问题规模n的增大,算法执行时间 的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称时间复杂度,其中f(n)是问题规模n的某个函数。
T(n)=O(f(n))
```
n:问题规模
Tn:核心函数执行次数
f(n):核心函数
O():算法时间复杂度的记法
```
在这里,我们需要明确一个事情:**函数执行次数=函数执行时间**
用大写O()来体现算法时间复杂度的记法,我们称之为大O记法。一般情况下,随着输入规模n的增大,T(n)增长最慢的算法为最优算法。 下面我们使用大O表示法来表示一些求和算法的时间复杂度:
算法一:
```
public function getSum100(){
$sum=0; //1次
$n=100; //2次
$sum = ($n+1)*$n/2 //1次
echo "1到100的和是:".$sum;
}
```
算法二:
```
public function get100Sum(){
$sum=0; //1次
$n=100; //1次
for ($i=1; $i=$n < ; $i++) {
$sum+=$i; //n次
}
echo "1到100的和是:".$sum;
}
```
算法三:
```
static function fun1(){
$sum=0; //1次
$j=100;
for($s = 1;$j<=$n;$s++){
for ($b=1;$b<=$j;$b++) {
$sum +=$b; //n^2次
}
}
}
```
如果忽略判断条件的执行次数和输出语句的执行次数,那么当输入规模为n时,以上算法执行的次数分别为:
**算法一:3次
算法二:n+2次
算法三:n^2+2次**
如果用大O记法表示上述每个算法的时间复杂度,应该如何表示呢?基于我们对函数渐近增长的分析,推导大O阶 的表示法有以下几个规则可以使用:
1.用常数1取代运行时间中的所有加法常数;
2.在修改后的运行次数中,只保留高阶项;
3.如果最高阶项存在,且常数因子不为1,则去除与这个项相乘的常数;
所以,上述算法的大O记法分别为:
**算法一:O(1)
算法二:O(n)
算法三:O(n^2)
**执行效率:O(1) > O(n) > O(n^2)**
## **2.常见的大O阶**
### **2.1线性阶**
一般含有非嵌套循环涉及线性阶,线性阶就是随着输入规模的扩大,对应计算次数呈直线增长,例如:
~~~
public function get100Sum(){
$sum=0; //1次
$n=100; //1次
for ($i=1; $i=$n < ; $i++) {
$sum+=$i; //n次
}
echo "1到100的和是:".$sum;
}
~~~
上面这段代码,它的循环的时间复杂度为O(n),因为循环体中的代码需要执行n次
### **2.2平方阶**
一般嵌套循环属于这种时间复杂度
~~~
static function fun1(){
$sum=0; //1次
$j=100;
for($s = 1;$j<=$n;$s++){
for ($b=1;$b<=$j;$b++) {
$sum +=$b; //n^2次
}
}
}
~~~
上面这段代码,n=100,也就是说,外层循环每执行一次,内层循环就执行100次,那总共程序想要从这两个循环 中出来,就需要执行100\*100次,也就是n的平方次,所以这段代码的时间复杂度是O(n^2).
### **2.3立方阶**
一般三层嵌套循环属于这种时间复杂度
~~~
static function fun1(){
$sum=0; //1次
$j=100;
for($s = 1;$j<=$n;$s++){
for ($b=1;$b<=$j;$b++) {
for ($a=1;$a<=$j;$a++) {
$sum +=$a; //n^3次
}
}
}
}
~~~
上面这段代码,n=100,也就是说,外层循环每执行一次,中间循环循环就执行100次,中间循环每执行一次,最 内层循环需要执行100次,那总共程序想要从这三个循环中出来,就需要执行100100100次,也就是n的立方,所 以这段代码的时间复杂度是O(n^3)
### **2.4 对数阶**
~~~
int i=1,n=100;
while(i<n){
i = i*2;
}
~~~
由于每次i\*2之后,就距离n更近一步,假设有x个2相乘后大于n,则会退出循环。由于是2^x=n,得到x=log(2)n,所 以这个循环的时间复杂度为O(logn);
对于对数阶,由于随着输入规模n的增大,不管底数为多少,他们的增长趋势是一样的,所以我们会忽略底数。
### **2.5 常数阶**
一般不涉及循环操作的都是常数阶,因为它不会随着n的增长而增加操作次数。例如:
~~~
public function getSum100(){
$n=100; //2次
$sum = ($n+2) //1次
}
~~~
上述代码,不管输入规模n是多少,都执行2次,根据大O推导法则,常数用1来替换,所以上述代码的时间复杂度 为O(1)
## **3.常见复杂度分析**
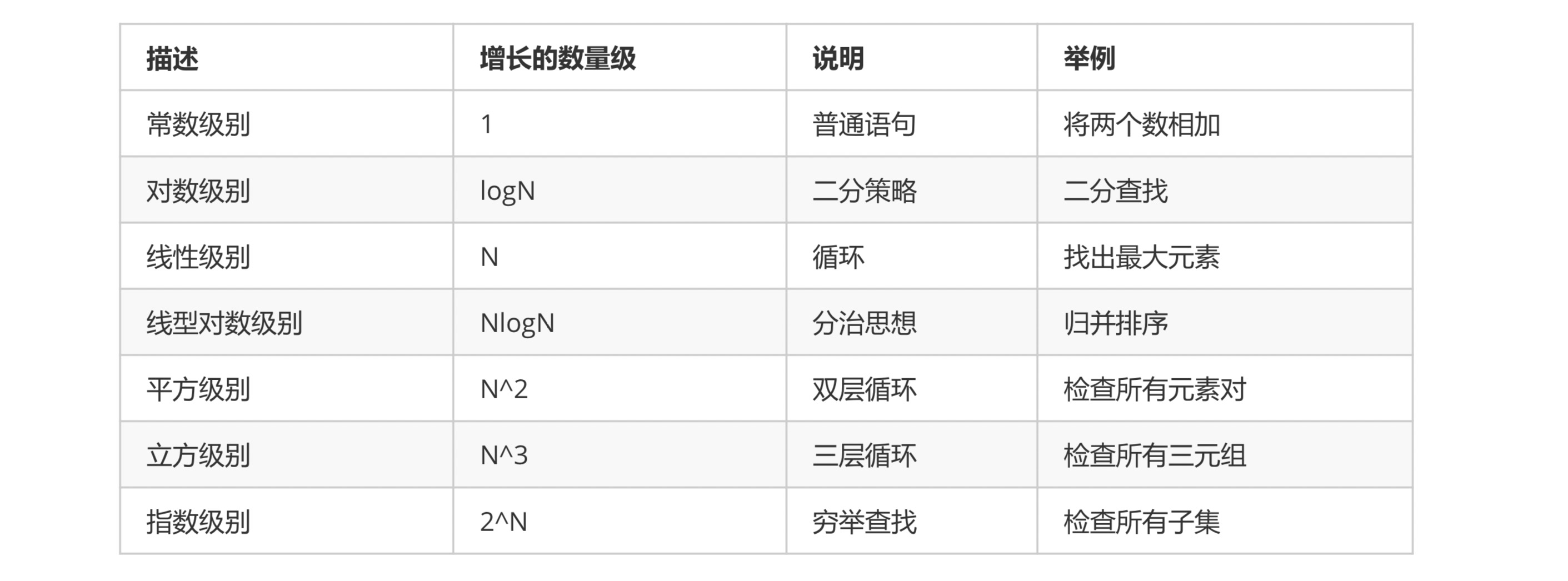
他们的复杂程度从低到高依次为:
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)
根据前面的折线图分析,我们会发现,从平方阶开始,随着输入规模的增大,时间成本会急剧增大,所以,我们的 算法,尽可能的追求的是O(1),O(logn),O(n),O(nlogn)这几种时间复杂度,而如果发现算法的时间复杂度为平方阶、 立方阶或者更复杂的,那我们可以分为这种算法是不可取的,需要优化。
