# 算法时间复杂度分析法
分析一个算法的时间复杂度有两种情况可以分析
1.写完之后看执行时间(事后分析估算方法:)
2.分析算法函数,得出算法时间复杂度(事前分析估算方法:)
**事后分析估算方法:**
比较容易想到的方法就是我们把算法执行若干次,然后拿个计时器在旁边计时,这种事后统计的方法看上去的确不 错,并且也并非要我们真的拿个计算器在旁边计算,因为计算机都提供了计时的功能。这种统计方法主要是通过设 计好的测试程序和测试数据,利用计算机计时器对不同的算法编制的程序的运行时间进行比较,从而确定算法效率 的高低,但是这种方法有很大的缺陷:必须依据算法实现编制好的测试程序,通常要花费大量时间和精力,测试完 了如果发现测试的是非常糟糕的算法,那么之前所做的事情就全部白费了,并且不同的测试环境(硬件环境)的差别 导致测试的结果差异也很大。
```
//可以直接通过时间差计算方法执行时间
static function getFunExTime(){
$t1=microtime(true);
for( $i=1;$i<=10000;$i++){
echo $i."*";
}
echo "<br>";
$t2=microtime(true);
echo $t1."<br>";
echo $t2."<br>";
echo "消耗时间:".round($t2-$t1,3);
}
```
**事前分析估算方法:**
很多时候,我们并不在算法实现之后再来对算法进行估算,我们需要在编写之前就对我们的算法进行估算。经过总结,我们发现一个高级语言编写的程序程序在计算机上运行所消耗的时间取决于下列因素:
1.算法采用的策略和方案;
2.编译产生的代码质量;
3.问题的输入规模(所谓的问题输入规模就是输入量的多少);
4.机器执行指令的速度;
**算法分析:**
由此可见,抛开这些与计算机硬件、软件有关的因素,一个程序的运行时间依赖于算法的好坏和问题的输入规模。
如果算法固定,那么该算法的执行时间就只和问题的输入规模有关系了。
那么再次以之前的求和案例为例,进行分析。
**需求:计算1到100的和。**
解法1:
```
//如果输入量为n为1,则需要计算1次;
//如果输入量n为1亿,则需要计算1亿次;
public function get100Sum(){
$sum=0;
$n=100;
for ($i=1; $i=$n < ; $i++) {
$sum+=$i;
}
echo "1到100的和是:".$sum;
}
```
解法2:
```
//如果输入量为n为1,则需要计算1次;
//如果输入量n为1亿,则需要计算1次;
public function getSum100(){
$sum=0;
$n=100;
$sum = ($n+1)*$n/2
echo "1到100的和是:".$sum;
}
```
因此,当输入规模为n时,第一种算法执行了1+1+(n+1)+n=2n+3次;第二种算法执行了1+1+1=3次。如果我们把 第一种算法的循环体看做是一个整体,忽略结束条件的判断,那么其实这两个算法运行时间的差距就是n和1的差距。
为什么循环判断在算法1里执行了n+1次,看起来是个不小的数量,但是却可以忽略呢?我们来看下一个例子:
**需求: 计算100个1+100个2+100个3+...100个100的结果**
代码:
```
static function fun1(){
$sum=0;
$j=100;
for($s = 1;$j<=$n;$s++){
for ($b=1;$b<=$j;$b++) {
$sum +=$b;
}
}
}
```
上面这个例子中,如果我们要精确的研究循环的条件执行了多少次,是一件很麻烦的事情,并且,由于真正计算和
的代码是内循环的循环体,所以,在研究算法的效率时,我们只考虑核心代码的执行次数,这样可以简化分析。
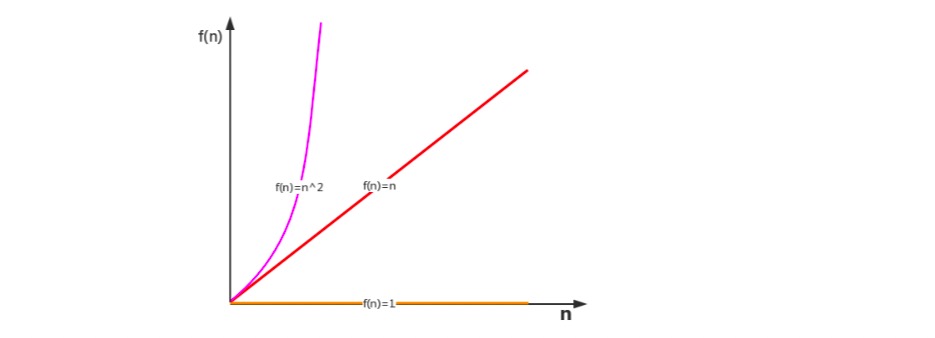
我们研究算法复杂度,侧重的是当输入规模不断增大时,算法的增长量的一个抽象(规律),而不是精确地定位需要 执行多少次,因为如果是这样的话,我们又得考虑回编译期优化等问题,容易主次跌倒。
我们不关心编写程序所用的语言是什么,也不关心这些程序将跑在什么样的计算机上,我们只关心它所实现的算
法。这样,不计那些循环索引的递增和循环终止的条件、变量声明、打印结果等操作,最终在分析程序的运行时间
时,最重要的是把程序看做是独立于程序设计语言的算法或一系列步骤。我们分析一个算法的运行时间,最重要的
就是把核心操作的次数和输入规模关联起来。