#### 第11章:
#### 数据结构
#### 11.1 什么是数据结构:
1. 数据
2. 数据元素
3. 数据对象
4. 数据结构
##### 数据
对客观事物的符号表示。在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号总称。对计算机的含义极为广泛,如图像、声音等都可以通过编码而归之于数据范畴。
##### 数据元素
数据的基本单位,在计算机程序中通常`作为一个整体`进行考虑和处理。
例如:一本书的书目信息为一个数据元素,而数目中的每一项(书名、作者名等)为一个`数据项`。`数据项是数据的不可分割的最小单位`。
##### 数据对象
`数据对象是性质相同的数据元素的集合`,是数据的一个子集。例如整数的数据对象是A={...,-4,-3,-2,-1,0,1,2,3,4,...},字母字符数据对象是C={A,B,C,D,E,...}。
##### 数据结构
`数据结构是相互之间存在一种或多种特定关系的数据元素的集合`。在任何问题中,数据元素都不是孤立存在的,而是在它们之间存在着某种关系,这种数据元素之间的关系称为结构。
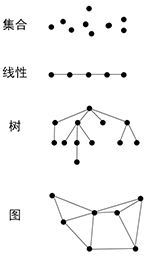
根据数据元素之间关系的不同特性,通常由下列4类基本结构:
1. `集合`
结构中的数据元素之间除了”同属一个集合“的关系外,别无其他关系。
2. `线性结构`
结构中的数据元素之间存在一个对一个的关系。
3. `树形结构`
结构中的元素之间存在一个对多个的关系。
4. `图状结构`或`网状结构`
5. 结构中的数据元素之间存在多个对多个的关系。
:-: 
结构定义中的”关系“描述的是数据元素之间的逻辑关系,因此又称为数据的逻辑结构。
数据结构在计算机中的表示(又称映像)称为数据的物理结构,又称存储结构。它包括数据元素的表示和关系的表示。
#### 11.2 算法
算法是对特定问题求解步骤的一种描述。它是指令的有限序列,其中每一条指令表示一个或多个操作。此外,一个算法还具有下列5个重要特性:
* 有穷性:一个算法必须总是在执行有穷步之后结束,且每一步都可在有穷时间内完成。
* 确定性:算法中每一条指令必须由确切的含义,读者理解时不会产生二义性。并且,在任何条件下,算法只有惟一的一条执行路径,即对于相同的输入只能得出相同的输出。
* 可行性:一个算法是能行的,即算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现的。
* 输入:一个算法有零个或多个输入,这些输入取自于某个特定的对象的集合。
* 输出:一个算法有一个或多个输出,这些输出是同输入有着某些特定关系的量。
##### 算法的设计要求
通常设计一个”好“的算法应该考量达到以下目标。
1. 正确性:算法应当满足具体问题的需求。正确一词分为4个层次,a.程序不含语法错误;b.程序对于几组输入数据能够得出满足规格说明要求的结果;c.程序对于精心选择的典型、苛刻而带有刁难性的几组输入数据能够得出满足规格说明要求的结果;d.程序对于一切合法的输入数据都能产生满足规格说明要求的结果。
2. 可读性:算法主要是为了人的阅读于交流,其次才是机器执行。可读性有助于人对算法的理解;晦涩难懂的程序易于隐藏较多错误,难以调试和修改。
3. 健壮性:当输入数据非法时,算法也能适当地做出反应或进行处理,而不是产生莫名奇妙地输出结果。
4. 效率与低储量需求:通俗地说,效率指的是算法的执行的时间。对于同一个问题如果有多个算法可以解决,执行时间短的算法效率高。存储量需求指算法执行过程中所需要的最大存储空间。效率与低存储量需求这两者都与问题的规模有关。
##### 算法的度量
1)事后统计的方法。
不做描述
2)事前分析估算的方法。
1. 依据算法选用何种策略。
2. 问题的规模,例如求100以内还是1000以内的素数。
3. 书写程序的语言,对于同一个算法,实现语言的级别越高,执行效率越低。
4. 编译程序所产生的机器代码的质量。
5. 机器执行指令的速度。
##### 算法的时间复杂度
一般情况,算法中基本操作重复执行的次数是问题规模n的某个函数f(n),算法的时间量度记作
**T(n)=O(f(n))**
它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,也叫做算法的`渐进时间复杂度`,简称时间复杂度。
语句的`频度`指的是该语句重复执行的次数。也就是原操作执行的次数。
(a)
~~~
{++x;s = 0}
~~~
(b)
~~~
for(i = 1;i<=n;++i){++x;s += x;}
~~~
(c)
~~~
for(j = 1; j<=n;++j)
for(k = 1;k<=n;++k){++x;s += x;}
~~~
以上三个程序中,含基本操作”x增1“的语句频度分别为1、n和n的2次方。则这三个程序段的时间复杂度分别为O(1),O(n),O(n的二次方)。分别称为`常量阶`、`线性阶`、`平方阶`。算法还能呈现的时间复杂度有`对数阶O(logn)`、`指数阶O(2的n次方)`。应该尽可能地选择`多项阶式O(n的k次方)`,而不希望用指数阶的算法。
##### 算法的空间复杂度
空间复杂度作为算法所需存储空间按的度量。
**S(n)=O(f(n))**
其中n为问题的规模(大小)。一个上机执行的程序除了需要存储空间来寄存本身所用的指令、常数、变量、和输入数据外,也需要一些对数据进行操作的工作单元和存储一些为实现所需信息的辅助空间。
#### 11.3 线性表
线性结构的特点是:在数据元素的非空有限集合中,(1)存在惟一的一个被称作”第一个“的数据元素(2)存在惟一的一个被称为”最后一个“的数据元素;(3)除第一个之外,集合中的每个数据元素均只有一个前驱;(4)除最后一个之外,集合中每个数据元素均只有一个后继。
**线性表**是最常用且最简单的一种数据结构。一个线性表是n个数据元素的有限序列。
例如:
26个英文字母的字母表:(A,B,C,···,Z)
某校从1976年到1983年各种类型计算机拥有量的变化情况:(6,17,28,50,92,188)
稍复杂的线性表中,一个数据元素可以由若干个`数据项`组成。在这种情况下,常把元素称为`记录`,含有大量记录的线性表又称为`文件`。
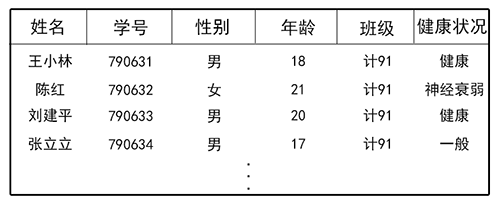
例如,一个学校的学生健康情况登记表,其中每个学生的情况为一个记录(一条数据元素由多条数据项组成)。它由姓名、学号、性别、年龄、班级、和健康等数据项组成。
:-: 
##### 线性表的顺序表现和实现
连续的存储单元:
线性表的顺序表示指的是用一组地址连续的存储单元顺序地存储线性表的数据元素。
##### 线性表的链式表示和实现
线性链表:
线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素(这组存储单元物理上可以是连续的,也可以是不连续的)。因此,为了表示每个数据元素a(i)与其a(i+1)之间的逻辑关系,对数据元素a(i)来说,除了存储本身的信息之外,还需要存储一个指向其直接后继的信息(即直接后继的存储位置),就要用到指针。这两部分组成了a(i)的存储映像,称为结点。这个结点包括两个域:`数据域`和`指针域`。
:-: 
##### 循环链表
循环链表最后结点的指针域指向头部结点。
##### 双向链表
双向链表有两个指针域,头指针域指向前一个结点,尾指针域指向下一个结点
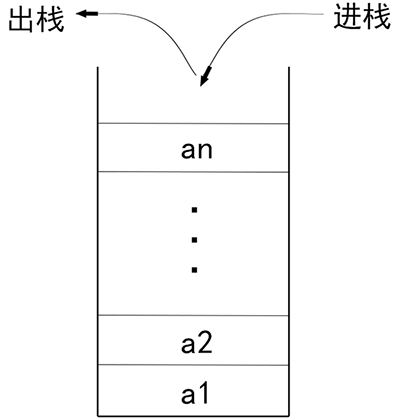
##### 栈
栈是计算机程序中非常重要的一种简单的线性结构。是一种先进后出的结构。
:-: 
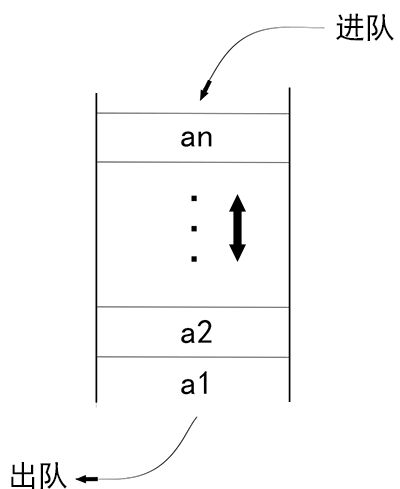
##### 队列
和栈相反,队列是先进先出。
:-: 
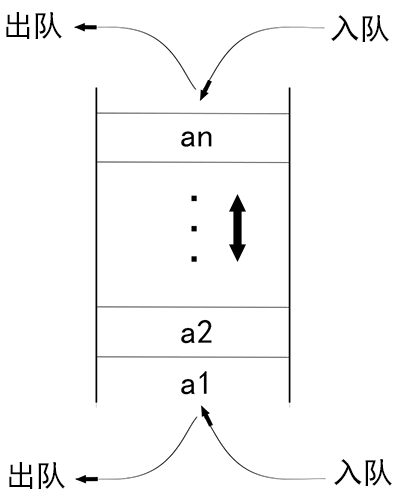
`双端队列`是一种限定插入和删除操作在表的两端进行的线性表。
:-: 
##### 循环队列
有兴趣的可以自己去查阅资料。
##### 串
串是由零个或多个字符组成的。
a=“BEI”;
b=“JING”;
c=“BEIJING”;
d=“BEI JING”;
#### 11.4 数组和广义表
前面讲的线性结构中的数据元素都是非结构性的原子类型,元素的值是不再分割的。
数组和广义表可以看成是线性表在此述含义中的扩展:表中的数据元素本身是一个数据结构。
:-: 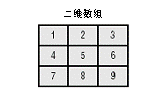
二维数组
:-: 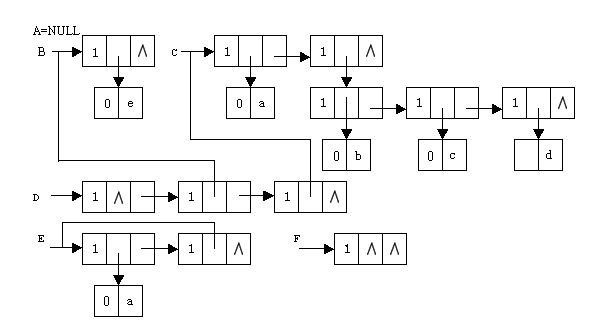
广义表
#### 11.5 树和二叉树
树形结构是一类重要的非线性数据结构。常用于数据库系统。其中树和二叉树最为常用,直观来看树是以分支关系定义的层次结构。树结构在客观世界中广泛存在,如人类社会的族谱和各种社会组织机构都可用树来形象表示。
关于树的概念:
1. 度:树的层次
2. 根:树最初的结点
3. 双亲和孩子:结点的子树根称为该结点的孩子。相应的,该结点称为孩子的双亲。
4. 祖先和子孙:以某结点为根的子树中的任一结点都称为该结点的子孙。反之,祖先是从根结点到该结点所经分支上的所有结点。
5. 叶子:没有子孙的结点。
:-: 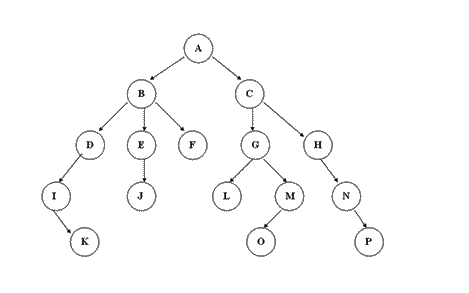
树
##### 树
树:
是n(n>=0)个结点的有限集。在任意一个非空树中:
1. 有且仅有一个特定的称为根的结点;(上图的A结点)
2. 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,T3 ····,其中每个集合本身又是一棵树,并且称为根的`子树`。
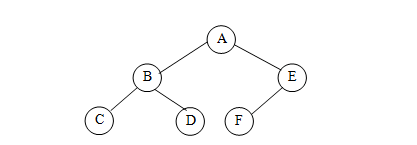
二叉树:
是另一种树型结构,它的特点是每个结点至多只有两颗子树。并且,二叉树的子树有左右之分,其次序不能任意颠倒。意思是在数据存储时应该遵循从左向右的原则。
:-: 
完全二叉树:
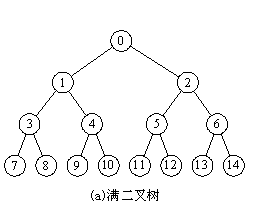
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树(比如满二叉树5和完全二叉树5的节点位置一样,其他的1234也都一样,就是完全二叉树。)。
:-: 
完全二叉树的结点数据存储表示(完全二叉树遵循从上到下从左到右原则)
满二叉树:
:-: 
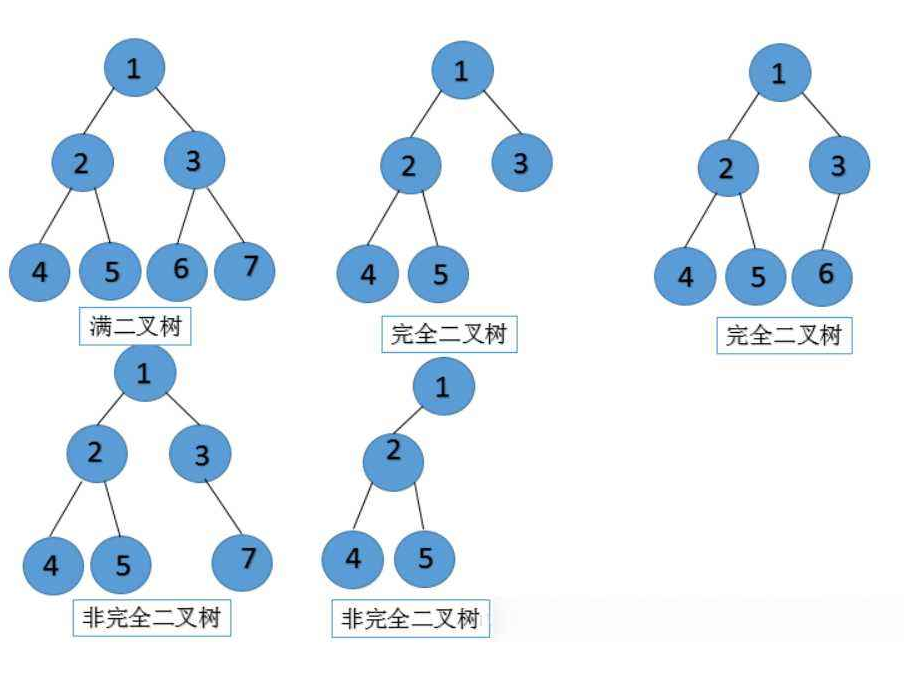
区别示意图:
:-: 
遍历二叉树:
:-: