# 13 可视化自变量的时间序列和其他函数
> 原文: [13 Visualizing time series and other functions of an independent variable](https://serialmentor.com/dataviz/time-series.html)
> 校验:[飞龙](https://github.com/wizardforcel)
> 自豪地采用[谷歌翻译](https://translate.google.cn/)
前一章讨论了散点图,其中我们根据一个定量变量绘制了另一个定量变量。当两个变量中的一个可以被认为是时间时会出现一种特殊情况,因为时间会对数据施加额外的结构。现在数据点具有固有的顺序;我们可以按照时间增加的顺序排列点,并为每个数据点定义前导和后继。我们经常希望用折线图来可视化这个时间顺序。然而,折线图不限于时间序列。只要数据可以按照一个变量排序,它们就是合适的。例如,在受控实验中也出现这种情况,其中治疗变量有目的地设定为一系列不同的值。如果我们有多个依赖于时间的变量,我们可以绘制单个折线图,也可以绘制规则的散点图,然后绘制直线来连接时间上相邻的点。
## 13.1 单个时间序列
作为时间序列的第一个演示,我们将考虑生物学预印本每月提交的模式。预印本是研究人员在正式同行评审和在科研期刊上发表之前,在线发表的学术文章。预印本服务器 bioRxiv 成立于 2013 年 11 月,专门面向从事生物科学研究的研究人员,自那以后,每月提交的作品大幅增长。我们可以通过制作一种散点图来可视化这种增长(第 12 章),其中我们绘制了代表每个月提交数量的点(图 13.1)。
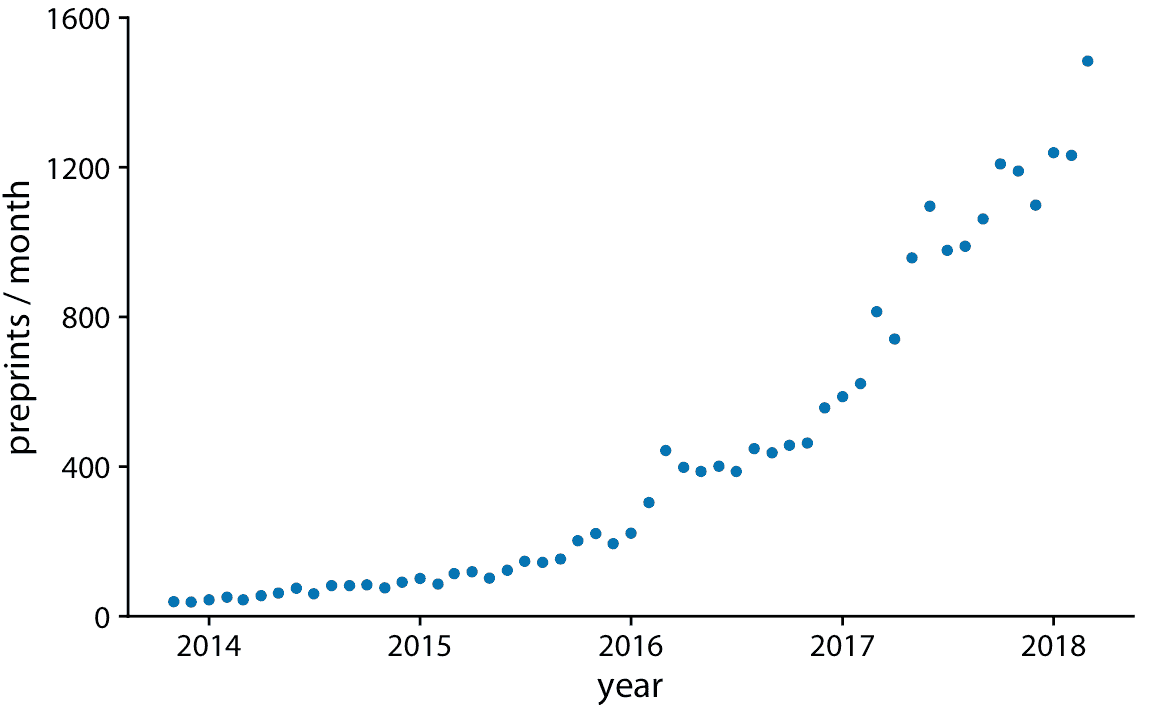
图 13.1:从 2014 年 11 月到 2018 年 4 月,预印本服务器 bioRxiv 的每月提交量。每个点代表一个月内提交量。在整个 4.5 年期间,提交量一直在稳步增加。数据来源:Jordan Anaya,[prepubmed.org](http://www.prepubmed.org/)
然而,图 13.1 与第 12 章中讨论的散点图之间存在重要差异。在图 13.1 中,点沿着 *x* 轴均匀分布,并且它们之间有一个确定的顺序。每个点只有一个左边和一个右边的邻居(除了最左边和最右边的点,每个点只有一个邻居)。我们可以通过用直线连接相邻点来在视觉上强调这个顺序(图 13.2)。这样的图被称为折线图。
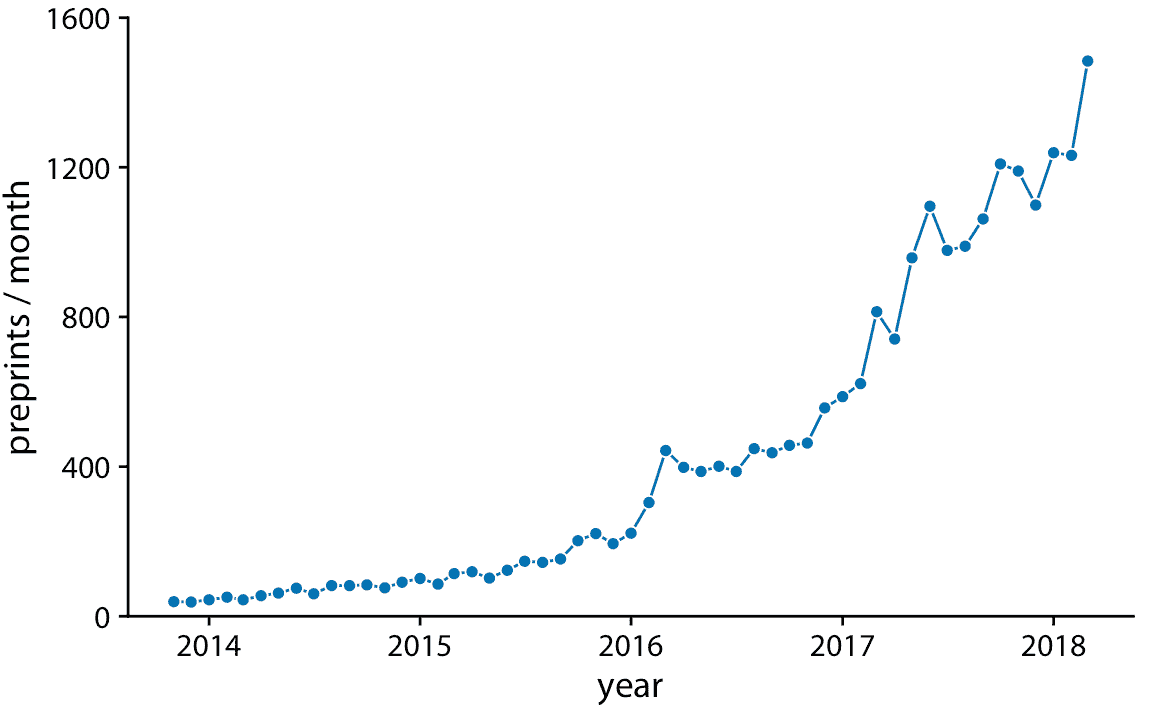
图 13.2:预印本服务器 bioRxiv 的每月提交量,显示为由线连接的点。这些线不代表数据,但仅作为眼睛的向导。通过用直线连接各个点,我们强调点之间有一个顺序,每个点恰好有一个前面的相邻点和后面的一个相邻点。数据来源:Jordan Anaya,[prepubmed.org](http://www.prepubmed.org/)
有些人反对在点之间绘制线条,因为线条不代表观察到的数据。特别是,如果只有很少的观测值,距离相隔很远,那么在中间时间进行观测时,它们可能不会精确地落在所示的线上。因此,在某种意义上,线对应于补充数据。然而,当点间隔很远或间距不均匀时,它们可能有助于感知。我们可以通过在图形标题中指出它来解决这个难题,例如通过写“直线作为眼睛的向导”(参见图 13.2 的标题)。
然而,使用直线来表示时间序列,并且通常完全省略点,是通常可接受的做法(图 13.3)。没有点,该图更加强调数据的整体趋势,而不是单个观测值。没有点的图形在视觉上也不那么嘈杂。一般来说,时间序列越密集,用点来表示单个观测值就越不重要。对于此处显示的预印本数据集,我认为省略这些点很好。
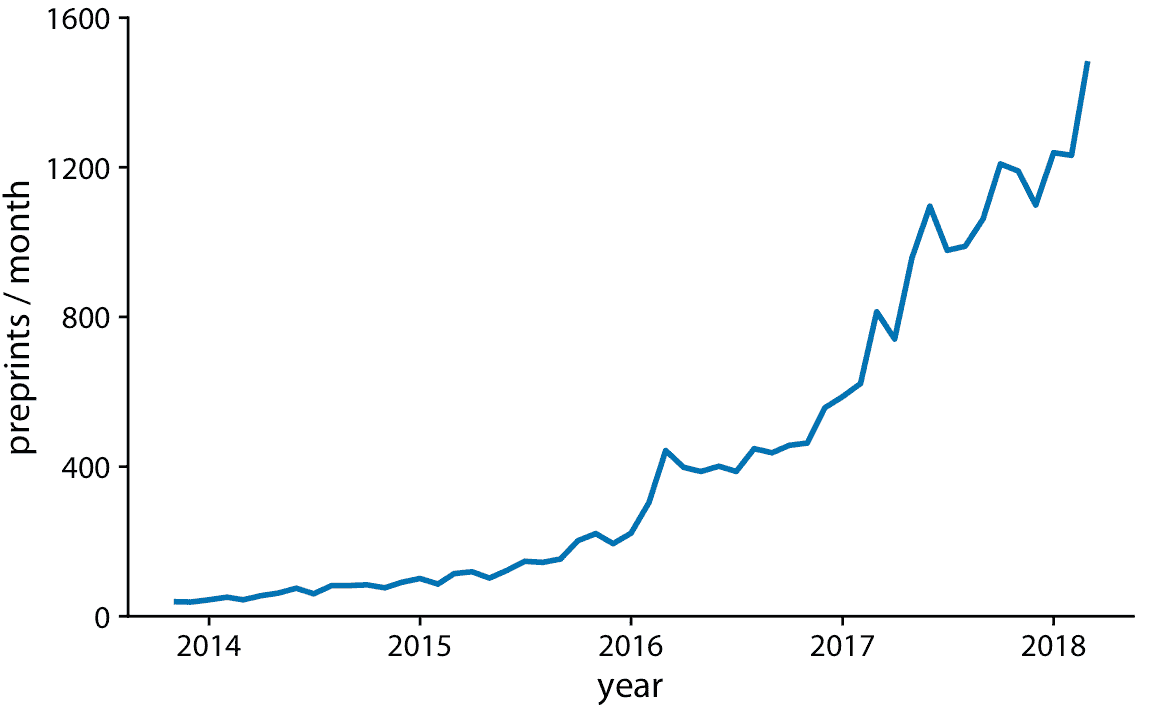
图 13.3:预印本服务器 bioRxiv 的每月提交量,显示为没有点的折线图。点的省略强调整体时间趋势,同时强调特定时间点处的个别观测值。当时间点的间隔非常密集时,它特别有用。数据来源:Jordan Anaya,[www.prepubmed.org](http://www.prepubmed.org/)
我们也可以用纯色填充曲线下区域(图 13.4 )。这种选择进一步强调了数据的总体趋势,因为它在视觉上将曲线上方的区域与下方区域分开。但是,此可视化仅在 *y* 轴从零开始时有效,因此每个时间点处的阴影区域高度表示该时间点的数据值。
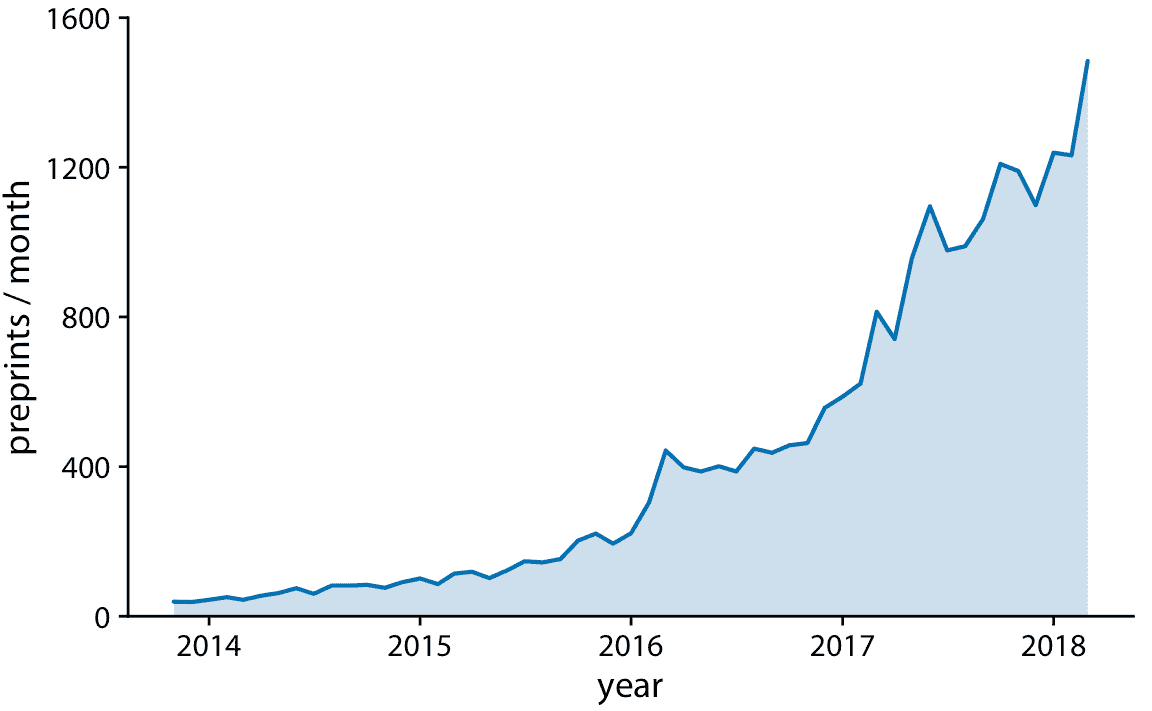
图 13.4:预印本服务器 bioRxiv 的每月提交量,显示为折线图和下侧填充区域。通过填充曲线下区域,我们更加强调总体时间趋势,而不是仅仅画一条线(图 13.3)。数据来源:Jordan Anaya,[prepubmed.org](http://www.prepubmed.org/)
## 13.2 多个时间序列和剂量反应曲线
我们经常有多个时间序列,我们想要一次显示它们。在这种情况下,我们必须更加谨慎地绘制数据,因为图形可能会变得混乱或难以阅读。例如,如果我们想要显示每月向多个预印本服务器提交的内容,则散点图不是一个好主意,因为各个时间序列相互碰撞(图 13.5)。用直线连接点可以缓解这个问题(图 13.6)。
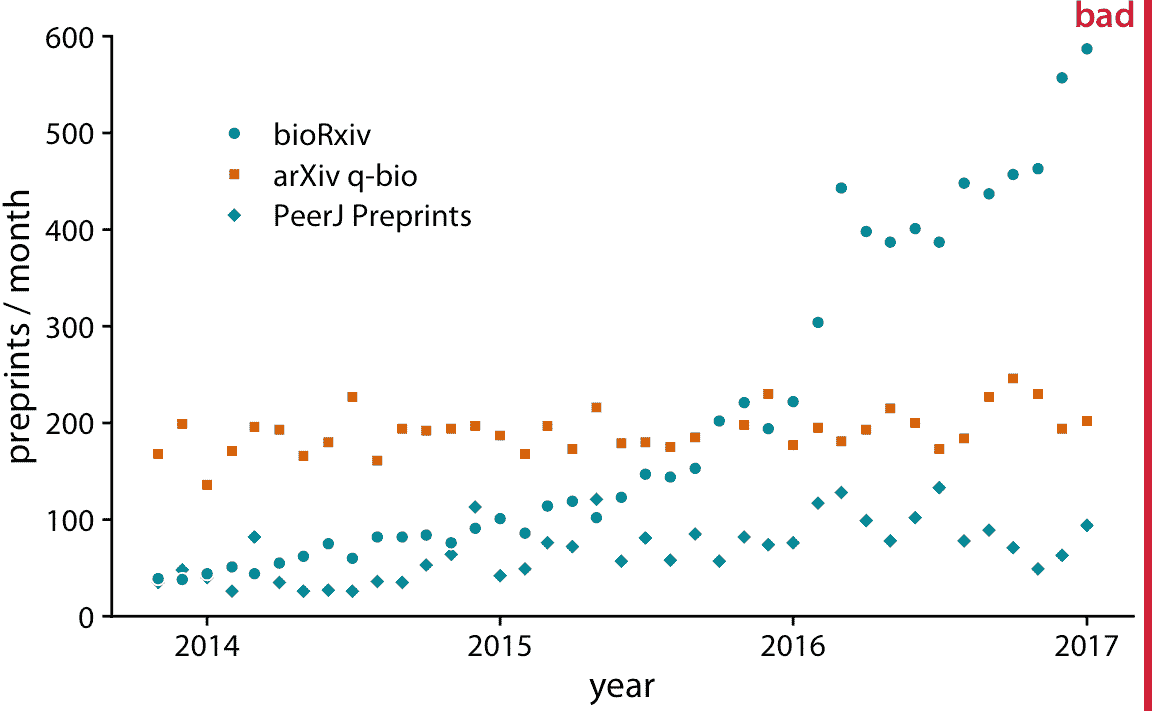
图 13.5:生物医学研究相关的三个预印本服务器的每月提交量:bioRxiv,arXiv 的 q-bio 部分和 PeerJ Preprints。每个点代表一个月内相应预印本服务器的提交数量。这个图形被标记为“不好”,因为这三个时间序列在视觉上相互干扰并且难以阅读。数据来源:Jordan Anaya,[prepubmed.org](http://www.prepubmed.org/)
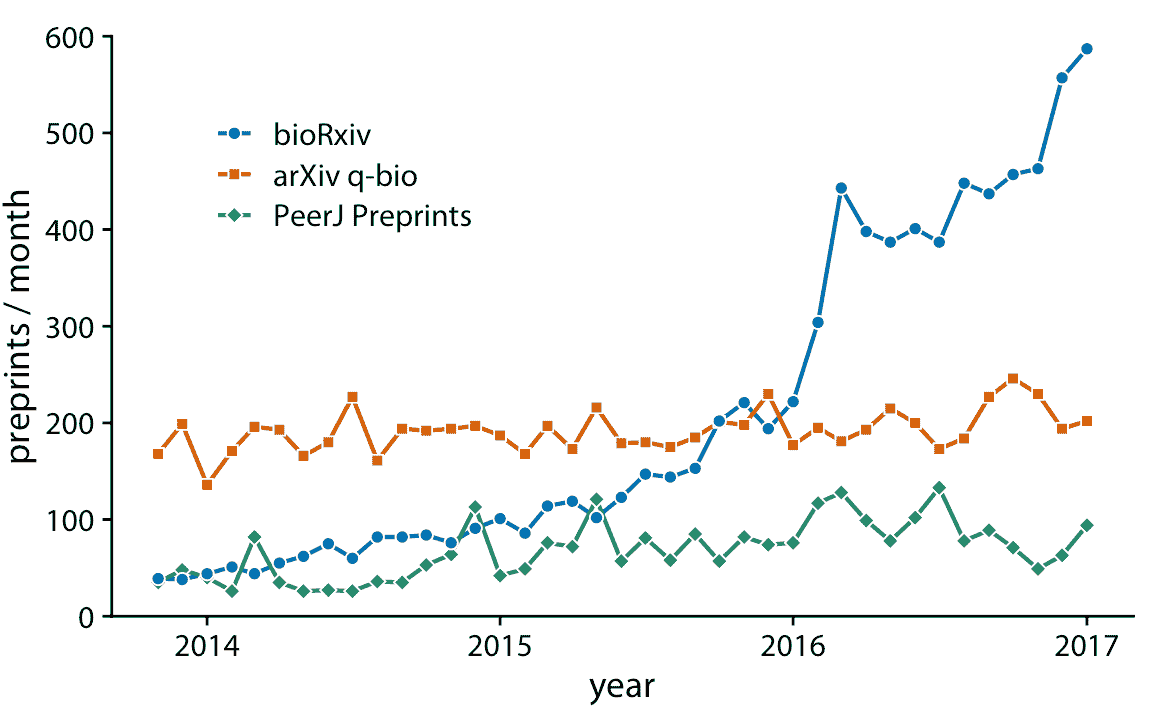
图 13.6:生物医学研究相关的三个预印本服务器的每月提交量。通过使用线连接图 13.5 中的点,我们帮助观众跟踪每个时间序列。数据来源:Jordan Anaya,[prepubmed.org](http://www.prepubmed.org/)
图 13.6 表示预印本数据集的可接受的可视化。但是,单独的图例会产生不必要的认知负担。我们可以通过直接标记线条来减少这种认知负担(图 13.7 )。我们还消除了该图中的各个点,结果比原始起点图 13.5 更加流畅和易读。
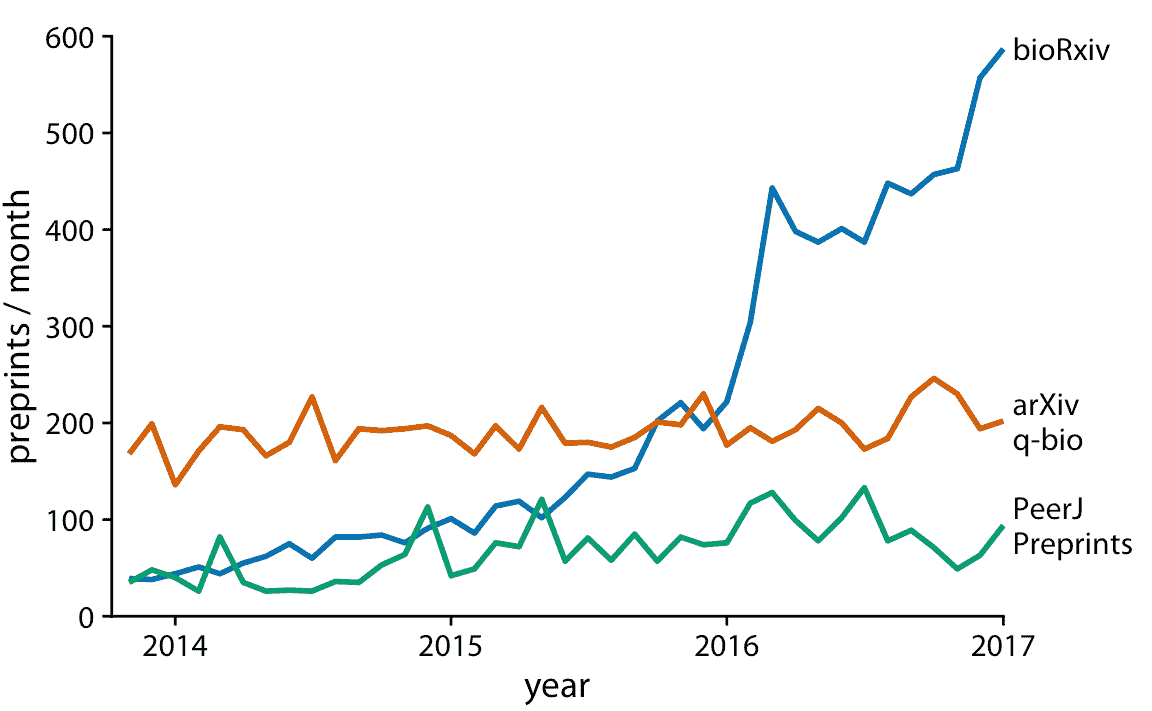
图 13.7:生物医学研究相关的三个预印本服务器的每月提交量。通过直接标记线条而不是提供图例,我们减少了读取图形所需的认知负担。消除图例消除了对不同形状点的需求。因此,我们可以通过消除点来进一步简化图形。数据来源:Jordan Anaya, [www.prepubmed.org](http://www.prepubmed.org/)
折线图不限于时间序列。只要数据点具有自然顺序,由沿 *x* 轴显示的变量反映,它们就是合适的,因此相邻点可以用线连接。例如,这种情况在剂量 - 反应曲线中出现,我们测量改变实验中的一些数值参数(剂量),如何影响感兴趣的结果(响应)。图 13.8 显示了这种类型的经典实验,根据增加的受精量来测量燕麦产量。折线图可视化突出了对于所考虑的三种燕麦品种,剂量 - 响应曲线如何具有相似的形状,但在没有受精的情况下起点不同(即一些品种具有比其他品种更高的产量)。

图 13.8:剂量 - 反应曲线显示了粪肥施肥后燕麦品种的平均产量。有了粪肥作为氮源,燕麦产量通常随着氮的增加而增加,无论品种是什么。这里,粪肥施用量以英担(cwt)计。英担是一个旧的英制单位,等于 112 磅或 50.8 千克。数据源:Yates(1935)
## 13.3 两个或多个响应变量的时间序列
在前面的例子中,我们只处理了一个响应变量的时间过程(例如,每月的预印本提交量或燕麦产量)。但是,拥有多个响应变量并不罕见。这种情况通常出现在宏观经济学中。例如,我们可能对过去 12 个月房价的变化感兴趣,因为它与失业率有关。我们可以预期,当失业率较低时房价会上涨,反之亦然。
鉴于前面小节中的工具,我们可以将这些数据可视化为两个相互叠加的独立折线图(图 13.9 )。该图直接显示了两个感兴趣的变量,并且可以直接解释。但是,因为这两个变量显示为单独的折线图,所以它们之间的绘图比较可能很麻烦。在两个变量在相同或相反的方向上移动时,如果我们想要识别时间区域,我们需要在两个图形之间来回切换并比较两条曲线的相对斜率。
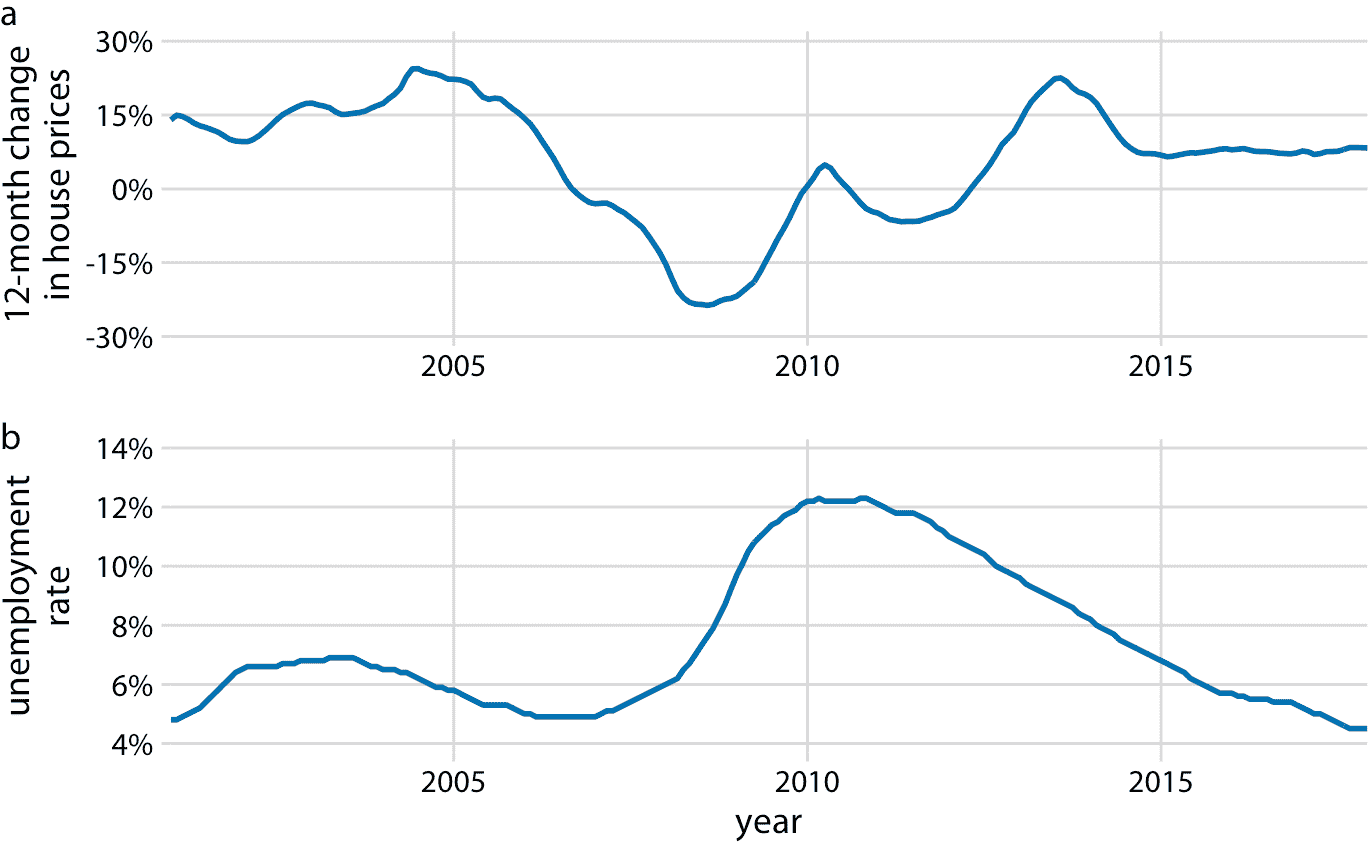
图 13.9:2001 年 1 月至 2017 年 12 月房价(a)和失业率(b)12 个月的随时间的变化。数据来源:美国劳工统计局 Freddie Mac 房价指数。
作为显示两个单独的折线图的替代方法,我们可以将两个变量相互绘制,绘制从最早的时间点到最晚的时间点的路径(图 13.10)。这种可视化被称为连通散点图,因为我们在技术上在汇智两个变量间的散点图,然后连接相邻点。物理学家和工程师经常将其称为相位图,因为在他们的学科中,它通常用于表示相位空间中的运动。我们之前在第三章中遇到了连通散点图,其中我们绘制了休斯顿,TX 的日常温度法线,与加利福尼亚州圣地亚哥的日常温度法线(图 3.3)。
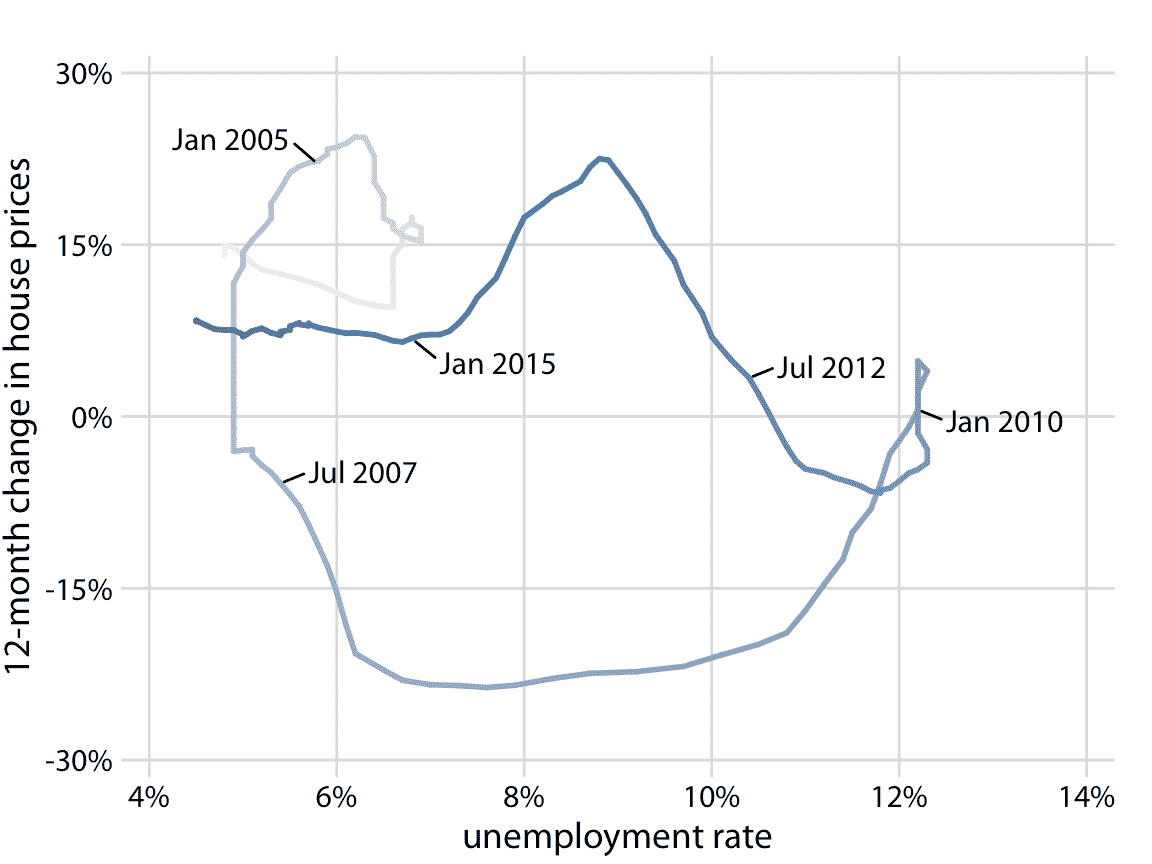
图 13.10:2001 年 1 月至 2017 年 12 月房价与失业率的 12 个月变化,显示为连通散点图。较暗的色调代表最近几个月。图 13.9 中看到的房价和失业率之间的负相关,导致连通散点图形成两个逆时针圆。数据来源:美国劳工统计局 Freddie Mac 房价指数。原始图概念:Len Kiefer
在连通散点图中,从左下角到右上角的方向上的线表示两个变量之间的相关运动(当一个变量增长时,另一个变量增长),并且从左上角到右下方沿垂直方向的线,表示负相关运动(随着一个变量增长,另一个变量收缩)。如果两个变量具有某种循环关系,我们将在连通散点图中看到圆或螺旋。在图 13.10 中,我们看到 2001 年至 2005 年的一个小圆圈和剩余时间过程的一个大圆圈。
绘制连通散点图时,重要的是我们指明数据的方向和时间刻度。如果没有这样的提示,绘图可能变成毫无意义的涂鸦(图 13.11)。(在图 13.10 中)我在这里使用逐渐变暗的颜色来指示方向。或者,可以沿着路径绘制箭头。
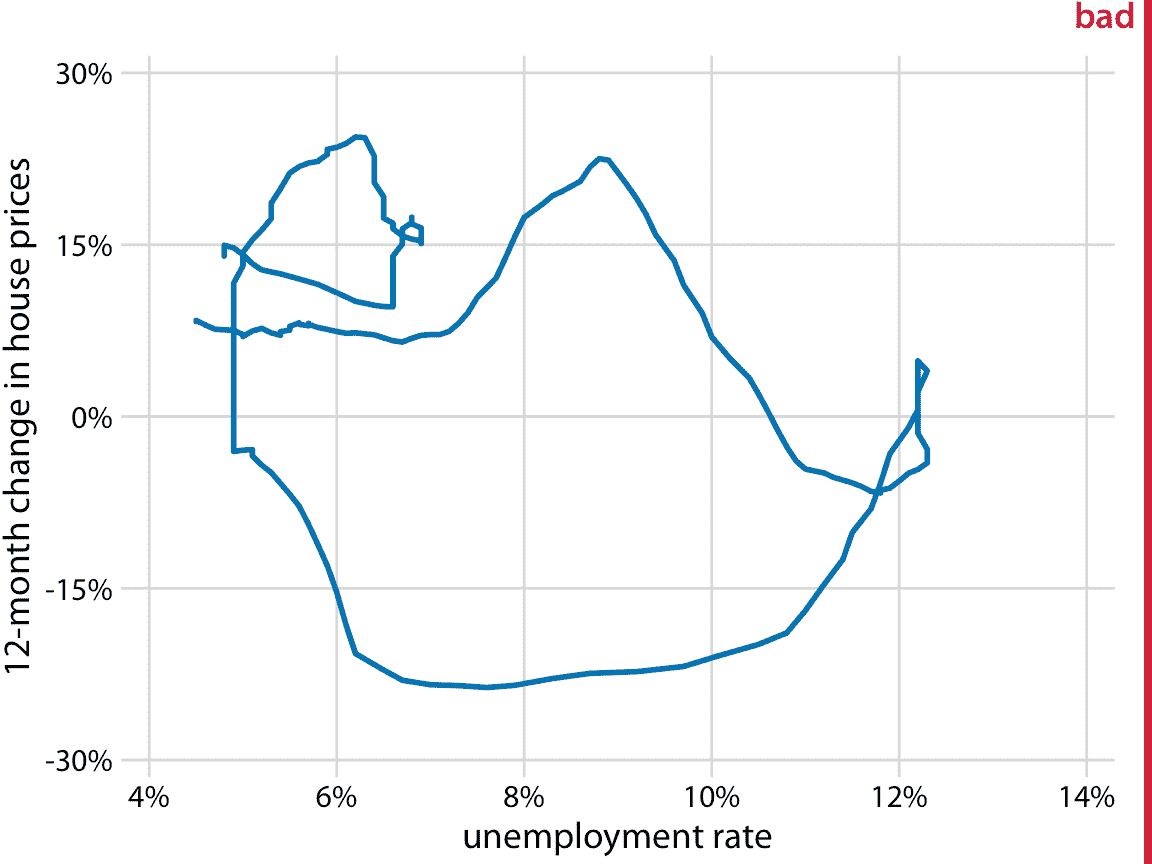
图 13.11:从 2001 年 1 月到 2017 年 12 月,房价与失业率的 12 个月变化。这个绘图被标记为“不好”,因为没有图 13.10 的日期标记和颜色渐变,我们既看不到数据的方向也看不到数据变化速度。数据来源:美国劳工统计局 Freddie Mac 价格指数。
使用连通散点图或两个单独的折线图哪个更好?单独的折线图往往更容易阅读,但是一旦人们习惯连通散点图,他们就可以提取某些模式(例如具有一些不规则性的循环行为),这些模式很难在折线图中找到。事实上,对我来说,房价变化和失业率之间的周期性关系很难在图 13.9 中看到,但图 13.10 中的逆时针螺旋清楚地表明了这一点。研究报告说,读者更容易混淆连通散点图,而不是折线图中的顺序和方向,并且不太可能看出相关性(Haroz,Kosara 和 Franconeri 2016)。另一方面,连通散点图似乎导致更高的参与度,因此这些图可能是吸引读者进入故事的有效工具(Haroz,Kosara 和 Franconeri 2016)。
即使连通散点图一次只能显示两个变量,我们也可以使用它们来可视化更高维的数据集。技巧是首先应用降维(见第 12 章)。然后,我们可以在低维空间中绘制连通散点图。作为这种方法的一个例子,我们将可视化由圣路易斯联邦储备银行提供的 100 多个宏观经济指标的月度观测值的数据库。我们对所有指标进行主成分分析(PCA),然后绘制 PC2 与 PC1(图 13.12a),以及 PC2 与 PC3(图 13.12b)的连通散点图。
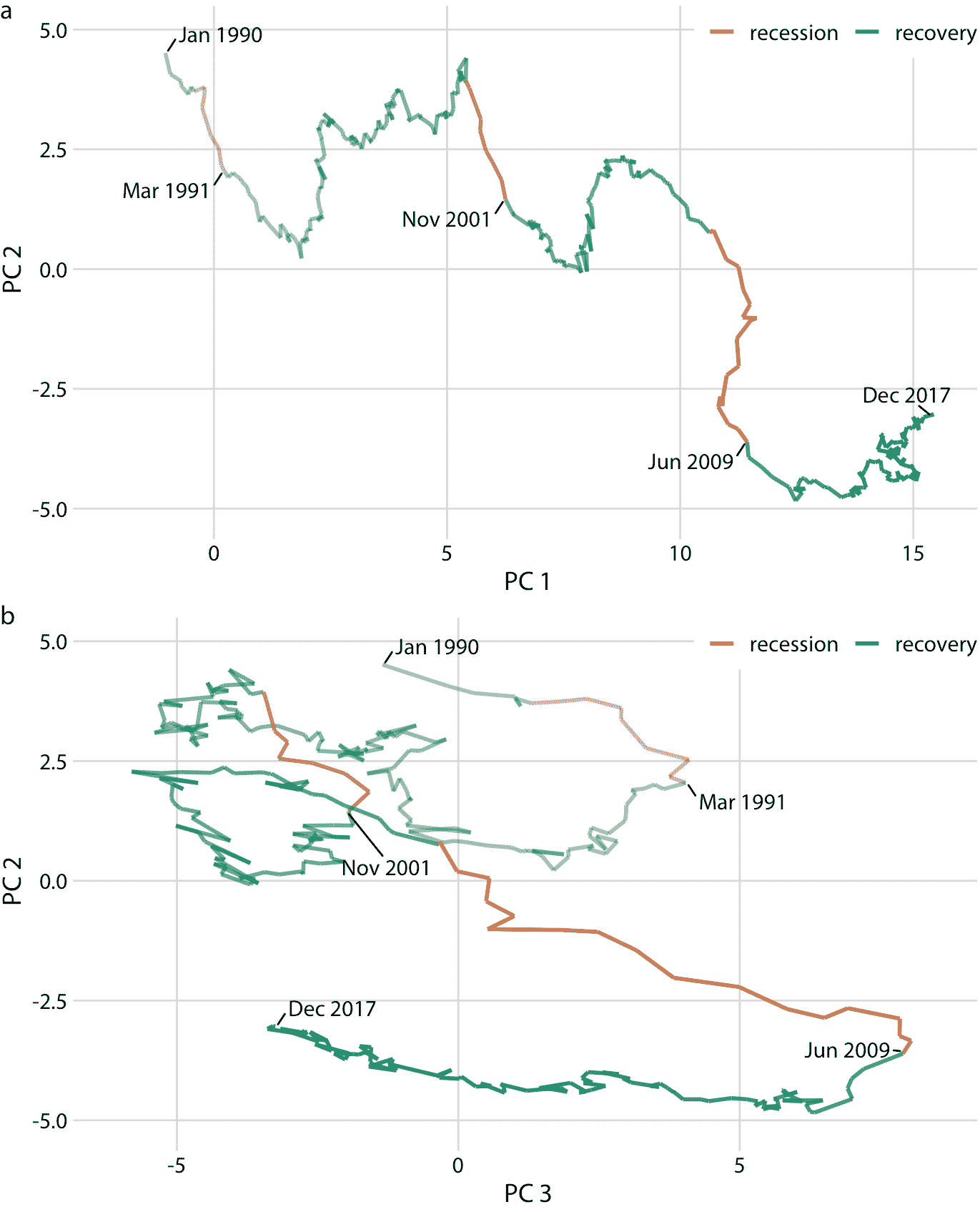
图 13.12:将高维时间序列可视化为主成分空间中的连通散点图。该绘图展示了 1990 年 1 月至 2017 年 12 月期间的 100 多个宏观经济指标的联合运动。经济衰退和复苏的时间以颜色表示,三次经济衰退的终点(1991 年 3 月,2001 年 11 月和 2009 年 6 月)也被标记。(a)PC2 与 PC1,(b)PC2 与 PC3。数据来源:M. W. McCracken,St. Louis Fed
值得注意的是,图 13.12a 看起来几乎像一个常规折线图,时间从左到右递增。这种模式是由 PCA 的一个共同特征引起的:第一个成分通常测量系统的总体规模。在这里,PC1 大致衡量经济的总体规模,这种规模很少随着时间的推移而减少。
通过按照衰退和复苏时间,对连通散点图进行着色,我们可以看到衰退与 PC2 下降有关,而复苏与 PC1 或 PC2 中的明显特征无关(图 13.12a)。然而,复苏似乎与 PC3 的下降相对应(图 13.12b)。此外,在 PC2 与 PC3 的图中,我们看到该线遵循顺时针螺旋的形状。这种模式突出了经济的周期性,经济复苏后出现衰退,反之亦然。
### 参考
```
Yates, F. 1935. “Complex Experiments.” Supplement to the Journal of the Royal Statistical Society 2: 181–247. doi:10.2307/2983638.
Haroz, S., R. Kosara, and S. Franconeri. 2016. “The Connected Scatterplot for Presenting Paired Time Series.” IEEE Transactions on Visualization and Computer Graphics 22: 2174–86. doi:10.1109/TVCG.2015.2502587.
```
- 数据可视化的基础知识
- 欢迎
- 前言
- 1 简介
- 2 可视化数据:将数据映射到美学上
- 3 坐标系和轴
- 4 颜色刻度
- 5 可视化的目录
- 6 可视化数量
- 7 可视化分布:直方图和密度图
- 8 可视化分布:经验累积分布函数和 q-q 图
- 9 一次可视化多个分布
- 10 可视化比例
- 11 可视化嵌套比例
- 12 可视化两个或多个定量变量之间的关联
- 13 可视化自变量的时间序列和其他函数
- 14 可视化趋势
- 15 可视化地理空间数据
- 16 可视化不确定性
- 17 比例墨水原理
- 18 处理重叠点
- 19 颜色使用的常见缺陷
- 20 冗余编码
- 21 多面板图形
- 22 标题,说明和表格
- 23 平衡数据和上下文
- 24 使用较大的轴标签
- 25 避免线条图
- 26 不要走向 3D
- 27 了解最常用的图像文件格式
- 28 选择合适的可视化软件
- 29 讲述一个故事并提出一个观点
- 30 带注解的参考书目
- 技术注解
- 参考
