# 17 比例墨水原理 > 原文： [17 The principle of proportional ink](https://serialmentor.com/dataviz/proportional-ink.html) > 校验：[飞龙](https://github.com/wizardforcel) > 自豪地采用[谷歌翻译](https://translate.google.cn/) 在许多不同的可视化场景中，我们通过图形元素的区域来表示数据值。例如，在条形图中，我们绘制的条形图从 0 开始并以它们代表的数据值结束。在这种情况下，数据值不仅编码为条形的终点，而且编码为条形的高度或长度。如果我们绘制一个以非 0 值开始的条形图，则条形终点和条形长度将传达矛盾的信息。这些数字在内部不一致，因为它们使用相同图形元素显示的两个不同值。将此与我们使用点来可视化数据值的情况进行对比。在这种情况下，该值仅编码为点的位置，而不是点的大小或形状。 每当我们使用图形元素（如条形，矩形，任意形状的阴影区域）或任何其他具有明显可视区域的元素时，都会出现类似的问题，这些元素可能与所显示的数据值一致或不一致。在所有这些情况下，我们需要确保没有不一致。这个概念被 Bergstrom 和 West 称为比例墨水原理（Bergstrom 和 West [2016](#ref-BergstromWest2016) ）： > **比例墨水原理**：可视化中的阴影区域大小需要与它们所代表的数据值成比例。 （通常的做法是使用“墨水”一词来指代偏离背景颜色的可视化的任何部分。这包括线条，点，阴影区域和文本。然而，在本章中，我们主要讨论的是阴影区域。）违反这一原则的情况非常普遍，特别是在大众媒体和金融界。 ## 17.1 沿线性轴可视化 我们首先考虑最常见的情景，即沿线性比例的数量可视化。图 17.1 显示夏威夷州的五个县的收入中位数。这是报纸文章中可能遇到的典型图像。快速浏览一下这个图形表明，夏威夷县非常贫穷，而檀香山县比其他县富裕得多。然而，图 17.1 相当具有误导性，因为所有条形都以 50,000 美元的收入中位数开始。因此，虽然每个条形的终点正确代表了每个县的实际收入中位数，但条形高度代表收入中位数超过 50,000 美元的程度，这是一个任意数字。并且人类感知是这样的：条形高度是我们在观察该图时所感知的关键数量，而不是条形终点相对于 *y* 轴的位置。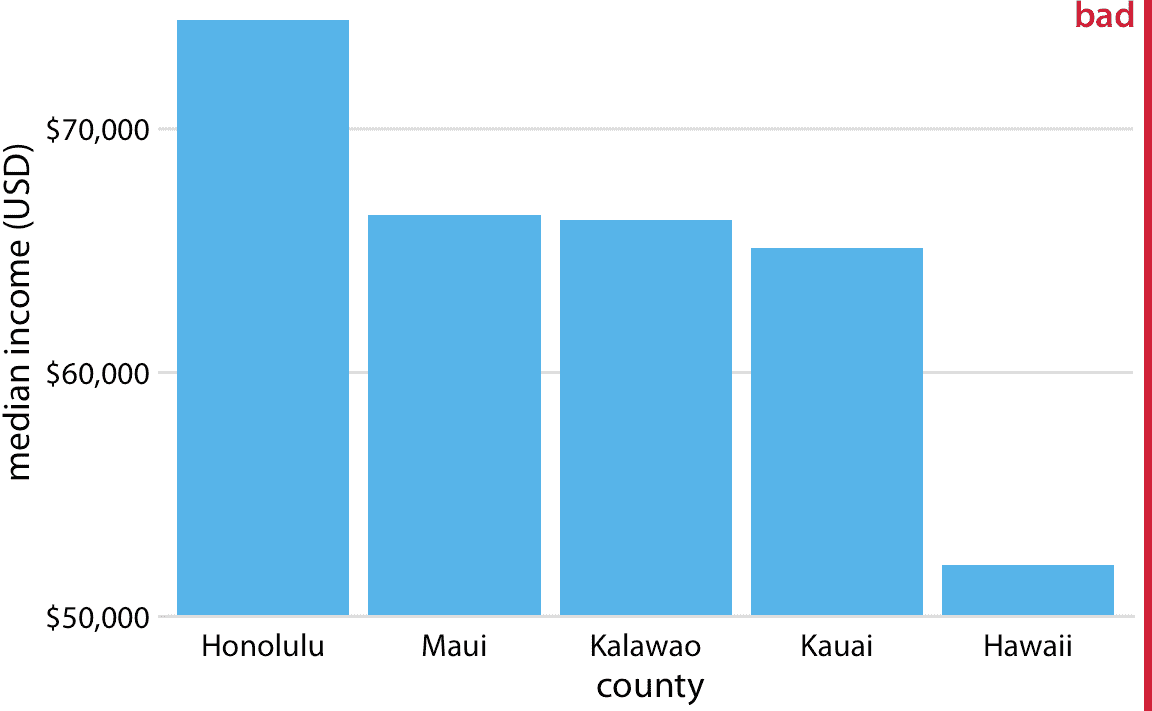  图 17.1：夏威夷州五个县的收入中位数。这个图形具有误导性，因为 *y* 轴刻度从 50,000 美元而不是 0 美元开始。结果，条形高度与所示数值不成比例，夏威夷县与其他四个县之间的收入差距看起来比实际大得多。数据来源：2015 年美国五年社区调查。 这些数据的适当可视化使得故事不那么令人激动（图 17.2 ）。虽然各州之间的收入中位数存在差异，但它们远远没有图 17.1 所暗示的那么大。总体而言，不同县的收入中位数是差不多的。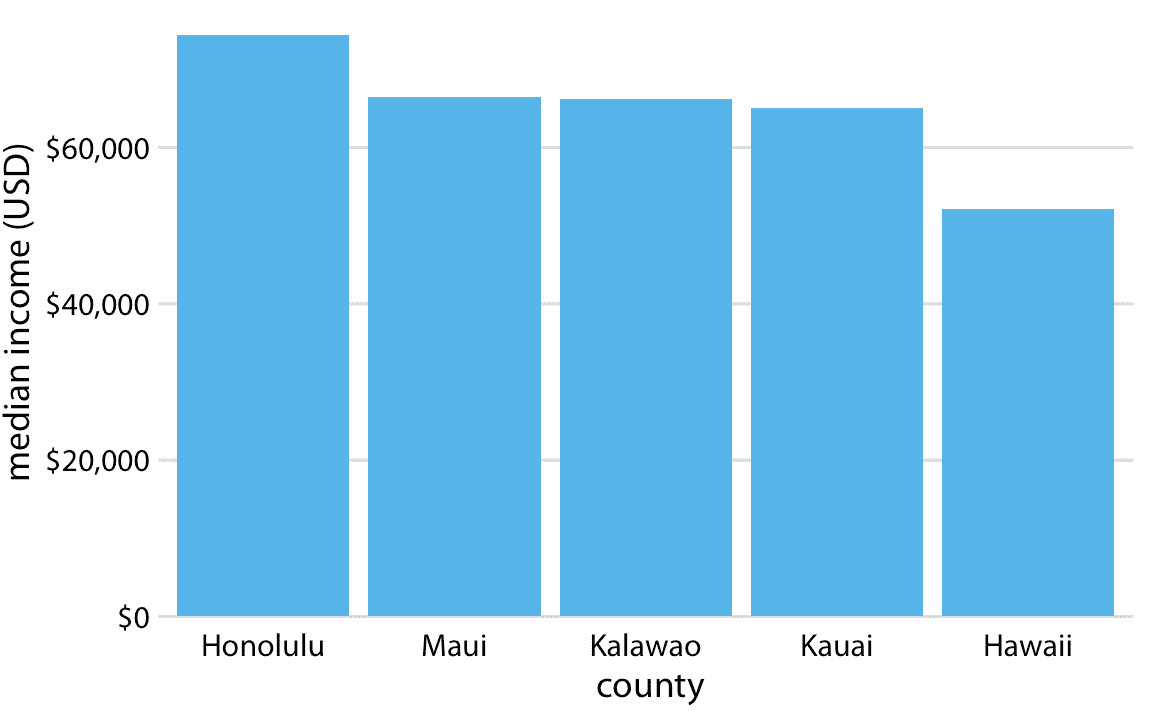  图 17.2：夏威夷州五个县的收入中位数。这里， *y* 轴刻度从 0 美元开始，因此准确显示了五个县的收入中位数的相对大小。数据来源：2015 年美国五年社区调查。 线性刻度上的条形应始终从 0 开始。 在时间序列的可视化中经常出现类似的可视化问题，例如股票价格的可视化问题。图 17.3 表明 Facebook 股票价格在 2016 年 11 月 1 日左右大幅下跌。实际上，相对于股票总价格，价格下跌幅度较小（图 17.4 ]）。即使没有曲线下方的阴影，图 17.3 中的 *y* 轴刻度也会有问题。但有了阴影，这个图形变得特​​别成问题。阴影强调从 *x* 轴的位置到所示的特定 *y* 值的距离，因此它产生视觉印象，即给定日期的阴影区域的高度代表那天的股票价格。相反，它只代表股票价格与基线的差异，图 17.3 中为 110 美元。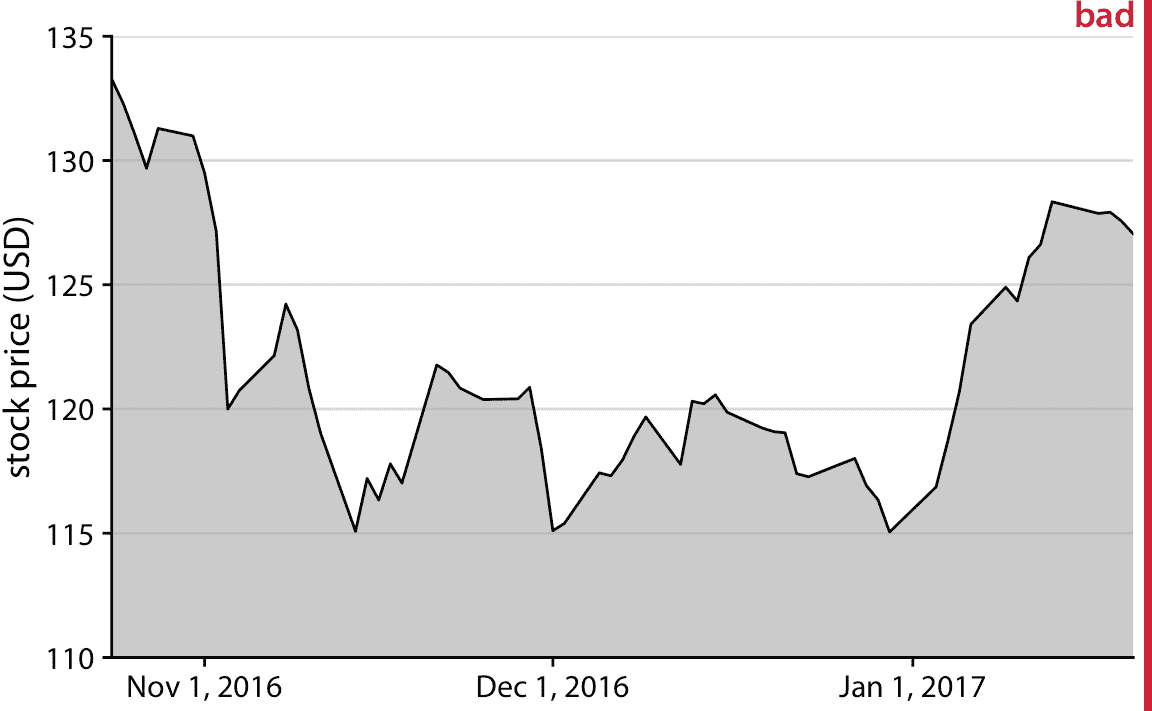  图 17.3：2016 年 10 月 22 日到 2017 年 1 月 21 日的 Facebook（FB）的股票价格。这个图形似乎意味着 Facebook 股票价格在 2016 年 11 月 1 日左右崩溃。但是，这是误导性的，因为 *y* 轴的起价为 110 美元而不是 0 美元。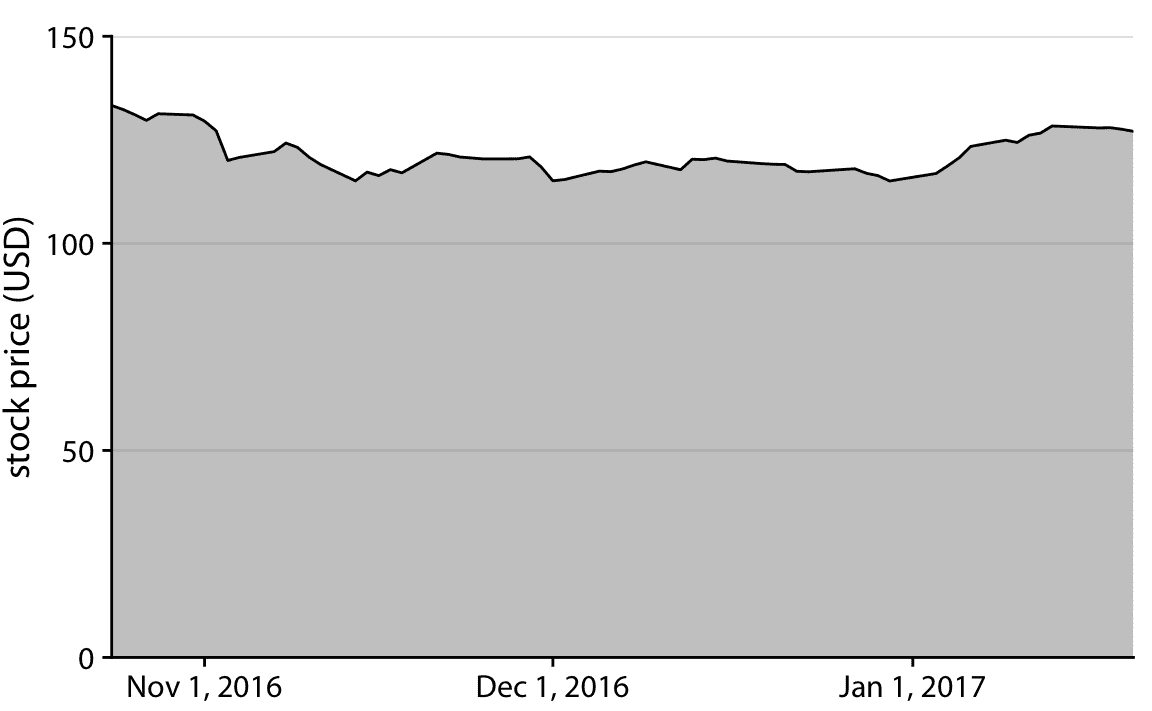  图 17.4：2016 年 10 月 22 日至 2017 年 1 月 21 日的 Facebook（FB）的股票价格。通过在 0 美元到 150 美元的 *y* 轴上展示的股票价格，这个图形更准确地传递了 2016 年 11 月 1 日左右的 FB 价格下跌的幅度。 图 17.2 和图 17.4 的例子可能表明，条形和阴影区域不能用于表示随时间的微小变化，或条件之间的差异，因为我们总是需要画出整个条形或从 0 开始的区域。但事实并非如此。使用条形或阴影区域来显示条件之间的差异是完全有效的，只要我们明确说明我们显示的差异。例如，我们可以使用条形图来显示 2010 年至 2015 年夏威夷县收入中位数的变化（图 17.5 ）。对于除卡拉沃以外的所有县，这一变化不到 5000 美元。 （卡拉沃是一个不同寻常的县，人口不到 100 人，少数人进出该县可能产生收入中位数的大幅波动。）对于夏威夷县，这种变化是负面的，即 2015 年的收入中位数低于 2010 年。我们通过绘制相反方向的条形来表示负值，即从 0 向下而不是向上延伸。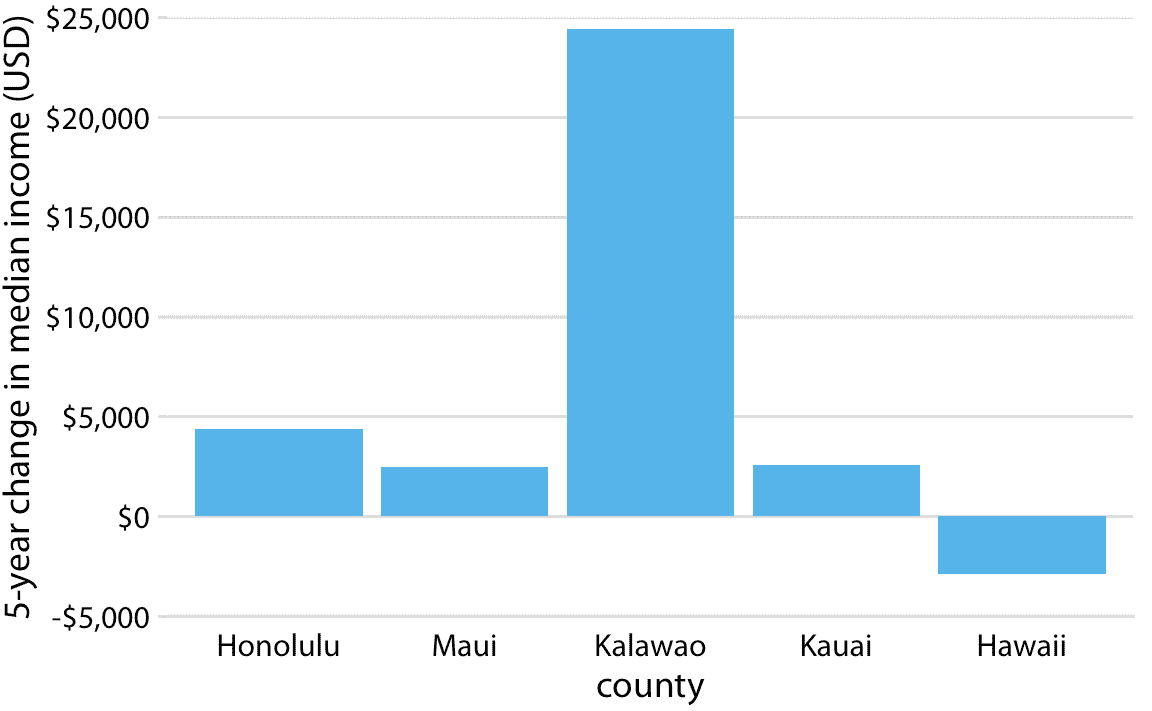  图 17.5：2010 年至 2015 年夏威夷县收入中位数的变化。数据来源：2010 年和 2015 年美国五年社区调查。 同样，我们可以将 Facebook 随时间变化的股票价格，绘制为与 2016 年 10 月 22 日的临时峰值的差异（图 17.6 ）。通过着色表示与峰值的距离的区域，我们可以准确地表示价格下降的绝对值，而不会对价格下降相对于总股价的幅度，做出任何隐含的陈述。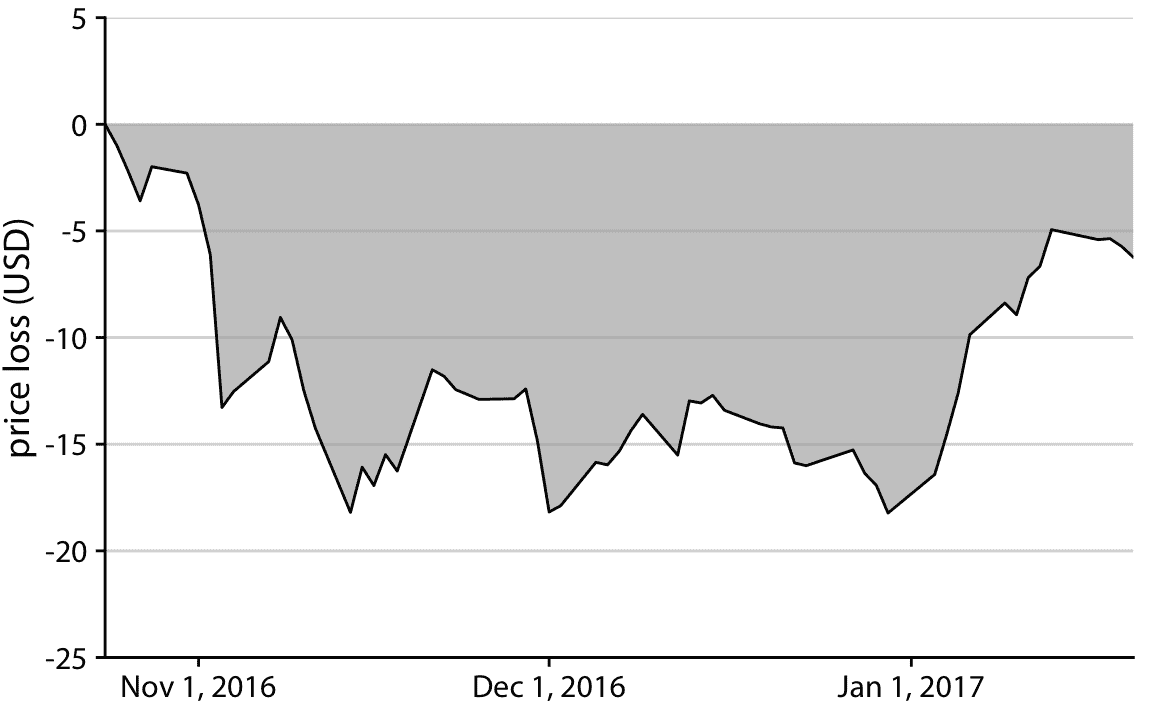  图 17.6：Facebook（FB）股票价格相对于 2016 年 10 月 22 日价格的损失。2016 年 11 月 1 日至 2017 年 1 月 1 日期间，价格比 2016 年 10 月 22 日的峰值低了约 15 美元。但随后价格在 2017 年 1 月开始复苏。 ## 17.2 沿对数轴的可视化 当我们沿线性刻度可视化数据时，条形，矩形或其他形状的区域自动与数据值成比例。如果我们使用对数刻度，则情况并非如此，因为数据值不是沿轴线性间隔的。因此，有人可能会争论说，例如，对数刻度上的条形图本质上存在缺陷。另一方面，每个条形的面积将与数据值的对数成比例，因此对数刻度上的条形图满足对数变换坐标中的比例墨水原理。在实践中，我认为这两个论点都不能解释对数比例条形图是否合适。相反，相关的问题是我们是否想要可视化数量或比率。 在第三章中，我已经解释了对数刻度是可视化比率的自然刻度，因为沿对数刻度的单位步长对应于乘以或除以常数因子。然而，在实践中，对数刻度通常并与专门用于可视化比率，而是因为显示的数字在很多数量级上变化。例如，考虑大洋洲国家的 2007 年国内生产总值（GDP），这些数字从不到 10 亿美元（USD）到超过 3000 亿美元不等（图 17.7）。以线性刻度可视化这些数字是行不通的，因为 GDP 最大的两个国家（新西兰和澳大利亚）将主导这一绘图。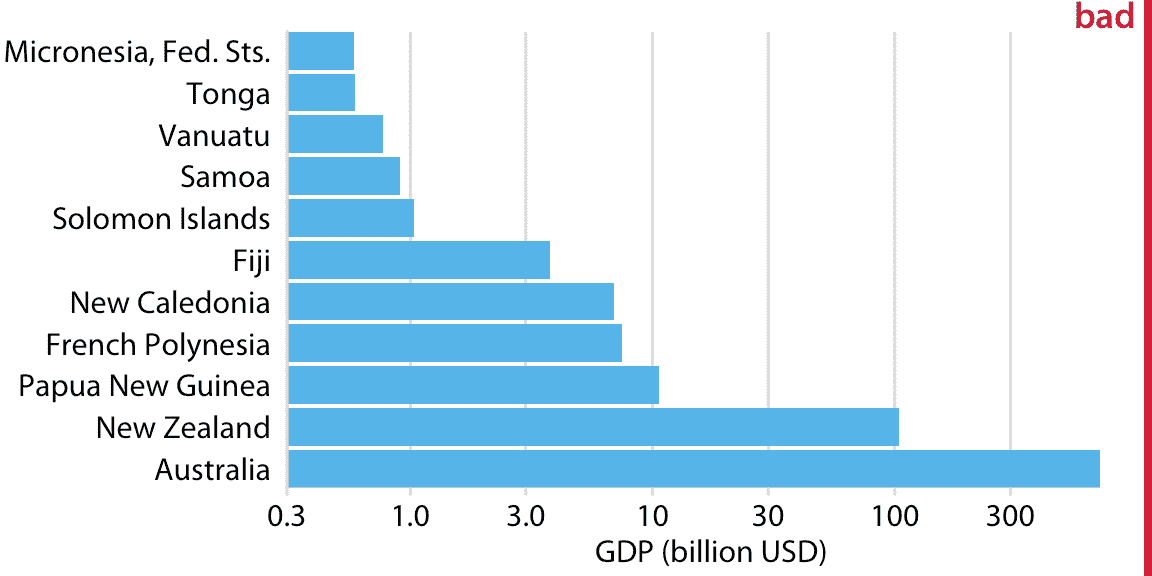  图 17.7：2007 年大洋洲国家的国内生产总值。条形的长度不能准确反映所显示的数据值，因为条形起始于 3 亿美元的任意值。数据来源：Gapminder。 但是，对数刻度上使用条形的可视化（图 17.7）也不起作用。条形起始于 3 亿美元的任意值，并且至少该绘图受到图 17.1 的相同问题的影响，条形长度不代表数据值。然而，对数刻度的额外难度在于我们不能简单地让条形从 0 开始。在图 17.7 中，值 0 将位于左侧无限远。因此，我们可以通过把它们的原点推得更远，来使我们的条形任意长，参见例如图 17.8 。当我们尝试在对数刻度上可视化数量（这是 GDP 值）时，总会出现这个问题。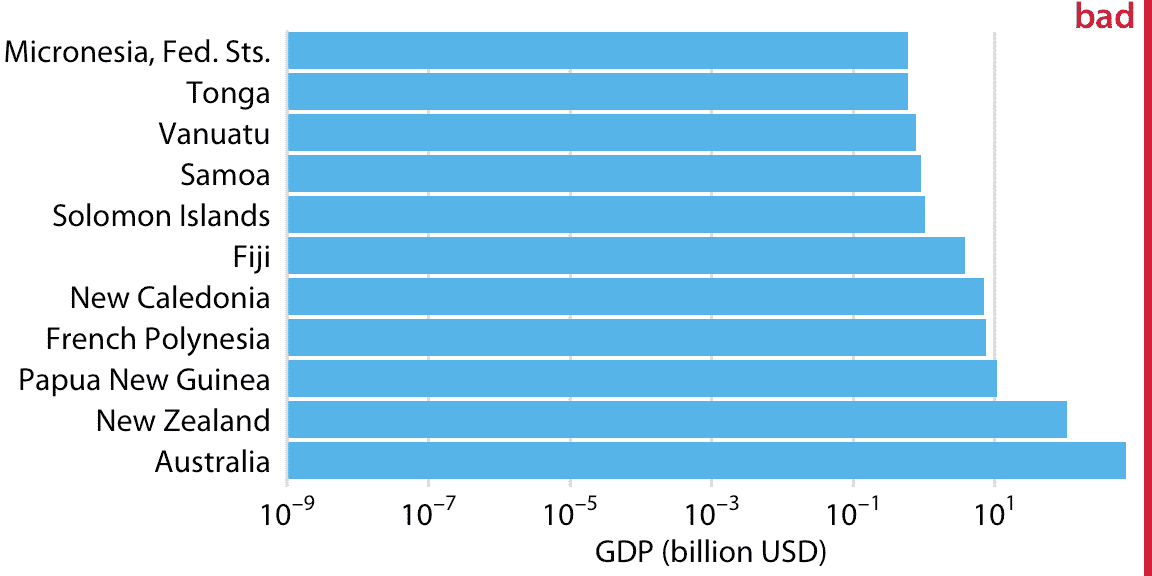  图 17.8：2007 年大洋洲国家的国内生产总值。条形的长度不能准确反映所示的数据值，因为条形起始于任意值 10^(-9) 十亿美元。数据来源：Gapminder。 对于图 17.7 的数据，我认为条形图是不合适的。相反，我们可以简单地沿着刻度，为每个国家的 GDP 在适当位置放置一个点，并完全避免条形长度问题（图 17.9 ）。重要的是，通过将国家名称放在点的旁边而不是沿着 *y* 轴，我们避免产生幅度的视觉感知，由国家名称到点的距离所传达。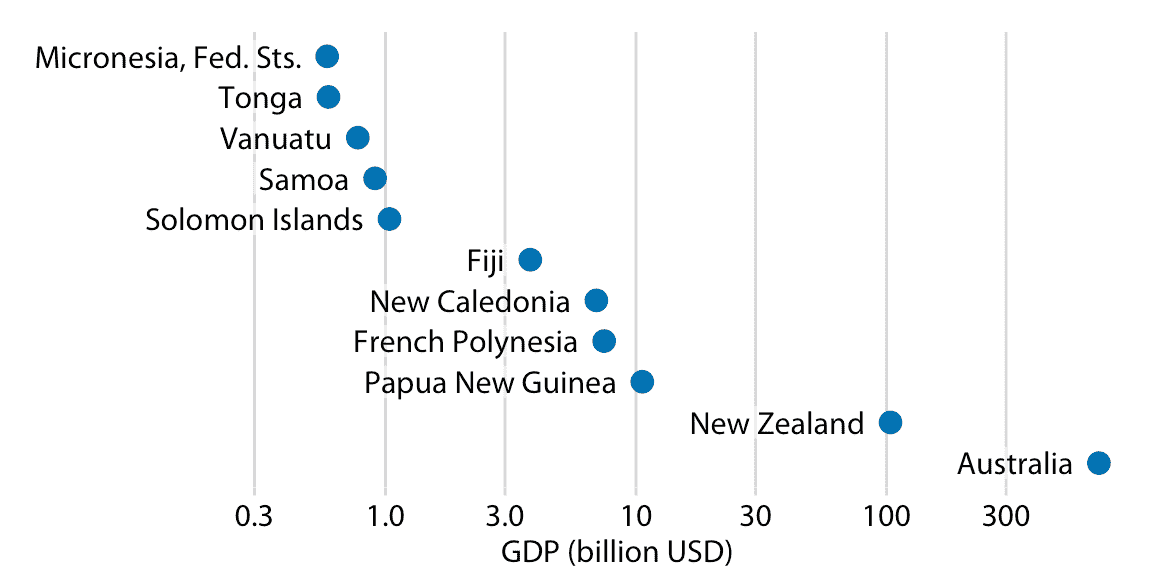  图 17.9：2007 年大洋洲国家的国内生产总值。数据来源：Gapminder。 但是，如果我们想要显示比率而不是数量，那么对数刻度上的条形是一个非常好的选择。实际上，在这种情况下，它们优于线性刻度上的条形。例如，让我们想象一下大洋洲国家的 GDP 值，相对于巴布亚新几内亚的 GDP。由此产生的绘图很好地突出了各国 GDP 之间的关键关系（图 17.10 ）。我们可以看到，新西兰的 GDP 超过巴布亚新几内亚的八倍，澳大利亚的 GDP 超过 64 倍，而汤加和密克罗尼西亚联邦的 GDP 不到巴布亚新几内亚国内生产总值的十六分之一。法属波利尼西亚和新喀里多尼亚相近，但 GDP 略低于巴布亚新几内亚。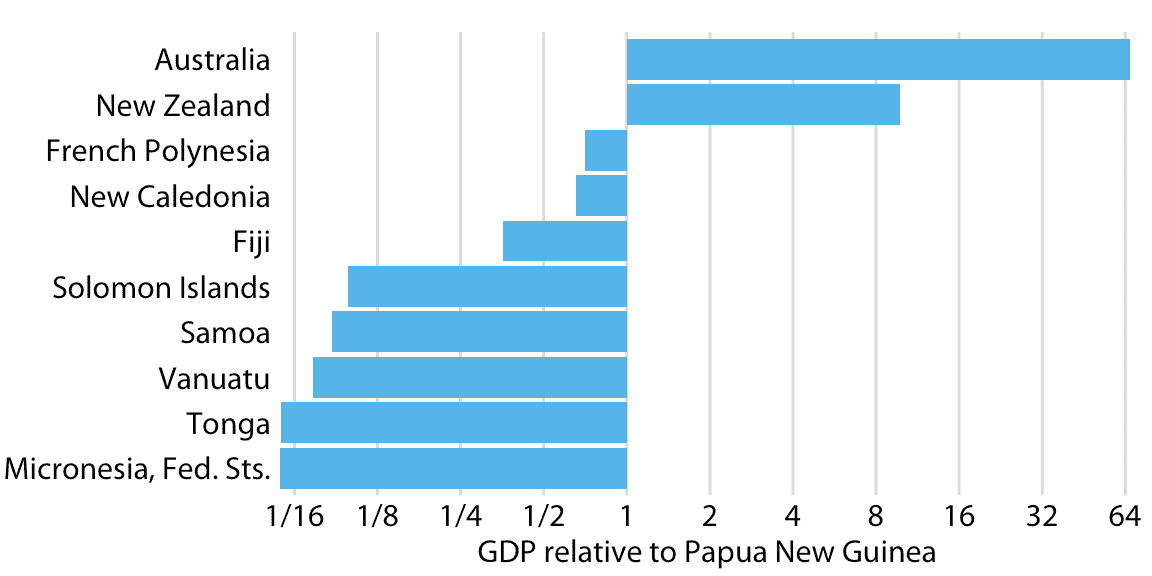  图 17.10：2007 年大洋洲国家的国内生产总值，相对于巴布亚新几内亚的国内生产总值。数据来源：Gapminder。 图 17.10 还突出显示对数刻度的自然中点为 1，表示大于 1 的数字的条形在一个方向上延伸，表示小于 1 的数字的条形在另一个方向上延伸条形。对数刻度上的条形表示比率，并且必须始终从 1 开始，线性刻度上的条形表示数量，并且必须始终从 0 开始。 在对数刻度上绘制条形时，它们表示比率，需要从 1 开始绘制，而不是 0。 ## 17.3 直接区域的可视化 所有前述示例沿一个线性维度可视化数据，使得数据值编码为沿着 *x* 或 *y* 轴的面积和位置。在这些情况下，我们可以将数据值的面积编码视为相对于位置编码的偶然和次要编码。然而，其他可视化方法主要或直接由面积表示数据值，而没有相应的位置映射。最常见的是饼图（图 17.11 ）。尽管从技术上讲，数据值被映射到角度，这些角度由沿着圆轴的位置表示，但实际上我们通常不会判断饼图的角度。相反，我们关注的主要视觉特性，是每个楔形区域的大小。  图 17.11：罗德岛县的居民人数，以饼图形示。每个楔形的角度和面积都与各个县的居民数量成比例。数据来源：2010 年美国十年普查。 因为每个楔形的面积与其角度成比例，该角度与楔形所代表的数据值成比例，所以饼图满足比例墨水原理。但是，我们认为饼图中的面积与条形图中的相同面积不同。根本原因是人类感知主要判断距离而不是面积。因此，如果数据值完全被编码为距离，如条形长度的情况，比起数据值编码为两三个距离的组合，它们共同创建一个区域的情况，我们更准确地感知它。为了看到这种差异，比较图 17.11 和图 17.12 ，它使用条形显示相同的数据。普罗维登斯县和其他县之间居民人数的差异在图 17.12 中比在图 17.11 中更大。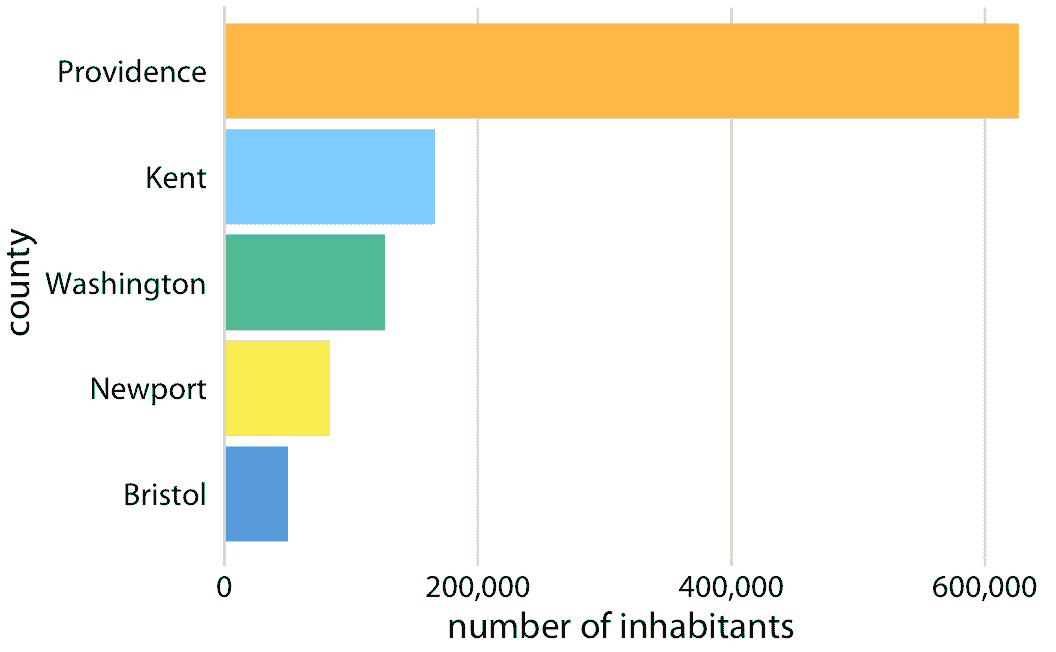  图 17.12：罗德岛县的居民人数，以条形图形示。每个条形的长度与各自县的居民数量成比例。数据来源：2010 年美国十年普查。 人类感知更善于判断距离而不是判断区域的问题，也出现在树形图中（图 17.13 ），可以将其视为饼图的方形版本。同样，与图 17.12 相比，各县居民数量的差异在图 17.13 中显得不太明显。  图 17.13：罗德岛县的居民人数，以树形图显示。每个矩形的面积与相应县的居民数量成比例。数据来源：2010 年美国十年普查。 ### 参考 ``` Bergstrom, C. T., and J. West. 2016. “The Principle of Proportional Ink.” http://callingbullshit.org/tools/tools_proportional_ink.html. ```