# 七、特征工程
> 作者:[Chris Albon](https://chrisalbon.com/)
>
> 译者:[飞龙](https://github.com/wizardforcel)
>
> 协议:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
## 稀疏特征矩阵上的降维
```py
# 加载库
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import TruncatedSVD
from scipy.sparse import csr_matrix
from sklearn import datasets
import numpy as np
# 加载数据
digits = datasets.load_digits()
# 标准化特征矩阵
X = StandardScaler().fit_transform(digits.data)
# 生成稀疏矩阵
X_sparse = csr_matrix(X)
# 创建 TSVD
tsvd = TruncatedSVD(n_components=10)
# 在稀疏矩阵上使用 TSVD
X_sparse_tsvd = tsvd.fit(X_sparse).transform(X_sparse)
# 展示结果
print('Original number of features:', X_sparse.shape[1])
print('Reduced number of features:', X_sparse_tsvd.shape[1])
'''
Original number of features: 64
Reduced number of features: 10
'''
# 前三个主成分的解释方差比之和
tsvd.explained_variance_ratio_[0:3].sum()
# 0.30039385372588506
```
## 核 PCA 降维
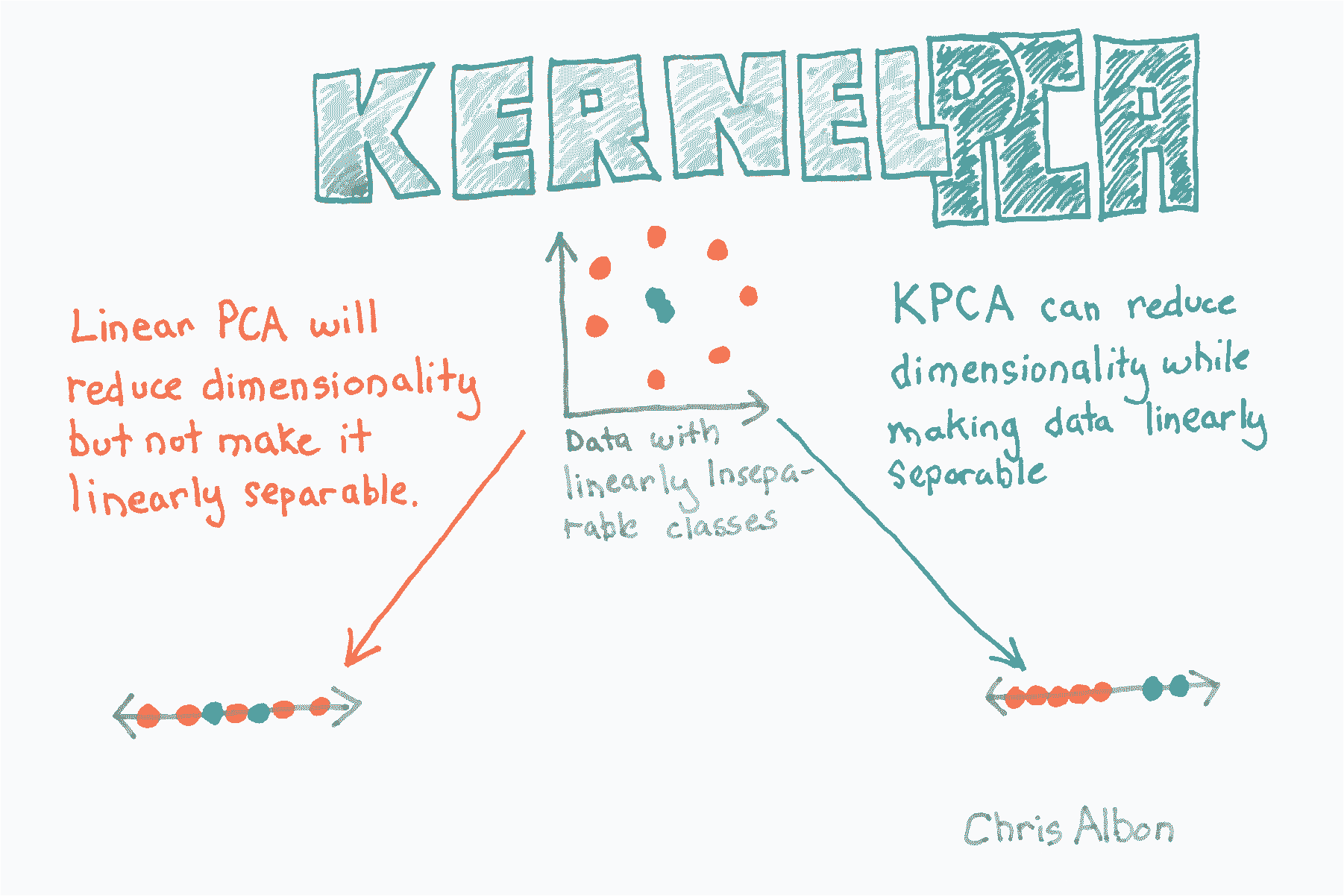
```py
# 加载库
from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circles
# 创建线性不可分的数据
X, _ = make_circles(n_samples=1000, random_state=1, noise=0.1, factor=0.1)
# 应用带有径向基函数(RBF)核的核 PCA
kpca = KernelPCA(kernel="rbf", gamma=15, n_components=1)
X_kpca = kpca.fit_transform(X)
print('Original number of features:', X.shape[1])
print('Reduced number of features:', X_kpca.shape[1])
'''
Original number of features: 2
Reduced number of features: 1
'''
```
## 使用 PCA 的降维
```py
# 加载库
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn import datasets
# 加载数据
digits = datasets.load_digits()
# 标准化特征矩阵
X = StandardScaler().fit_transform(digits.data)
# 创建保留 99% 方差的 PCA
pca = PCA(n_components=0.99, whiten=True)
# 使用 PCA
X_pca = pca.fit_transform(X)
# 展示结果
print('Original number of features:', X.shape[1])
print('Reduced number of features:', X_pca.shape[1])
'''
Original number of features: 64
Reduced number of features: 54
'''
```
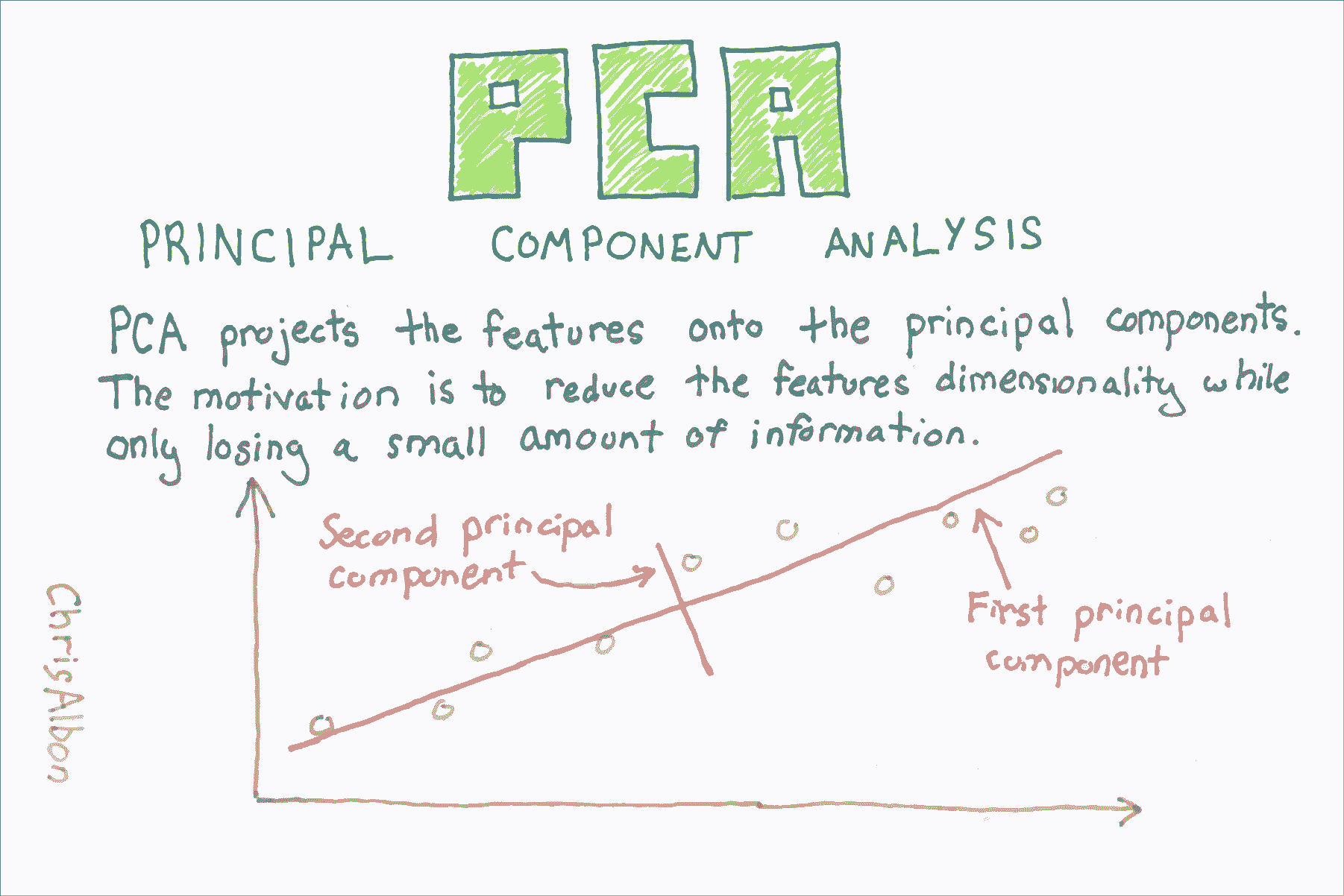
## PCA 特征提取
[主成分分析](https://en.wikipedia.org/wiki/Principal_component_analysis)(PCA)是数据科学中常见的特征提取方法。 从技术上讲,PCA 找到具有最高特征值的协方差矩阵的特征向量,然后使用这些特征向量将数据投影到相等或更小维度的新子空间。 实际上,PCA 将 n 个特征矩阵转换为(可能)小于 n 个特征的新数据集。 也就是说,它通过构造新的较少变量来减少特征的数量,这些变量捕获原始特征中找到的信息的重要部分。 但是,本教程的目的不是要解释 PCA 的概念,这在其他地方做得非常好,而是用于演示 PCA 的实际应用。
```py
# 导入库
import numpy as np
from sklearn import decomposition, datasets
from sklearn.preprocessing import StandardScaler
# 加载乳腺癌数据集
dataset = datasets.load_breast_cancer()
# 加载特征
X = dataset.data
```
请注意,原始数据包含 569 个观测和 30 个特征。
```py
# 查看数据集的形状
X.shape
# (569, 30)
```
这里是数据的样子
```py
# 查看数据
X
'''
array([[ 1.79900000e+01, 1.03800000e+01, 1.22800000e+02, ...,
2.65400000e-01, 4.60100000e-01, 1.18900000e-01],
[ 2.05700000e+01, 1.77700000e+01, 1.32900000e+02, ...,
1.86000000e-01, 2.75000000e-01, 8.90200000e-02],
[ 1.96900000e+01, 2.12500000e+01, 1.30000000e+02, ...,
2.43000000e-01, 3.61300000e-01, 8.75800000e-02],
...,
[ 1.66000000e+01, 2.80800000e+01, 1.08300000e+02, ...,
1.41800000e-01, 2.21800000e-01, 7.82000000e-02],
[ 2.06000000e+01, 2.93300000e+01, 1.40100000e+02, ...,
2.65000000e-01, 4.08700000e-01, 1.24000000e-01],
[ 7.76000000e+00, 2.45400000e+01, 4.79200000e+01, ...,
0.00000000e+00, 2.87100000e-01, 7.03900000e-02]])
'''
# 创建缩放器对象
sc = StandardScaler()
# 使缩放器拟合特征并转换
X_std = sc.fit_transform(X)
```
请注意,PCA 包含一个参数,即成分数。 这是输出特征的数量,需要进行调整。
```py
# 创建 PCA 对象,使用两个成分作为参数
pca = decomposition.PCA(n_components=2)
# 拟合 PCA 并转换数据
X_std_pca = pca.fit_transform(X_std)
```
在 PCA 之后,新数据已降到了两个特征,其行数与原始特征相同。
```py
# 查看新特征数据的形状
X_std_pca.shape
# (569, 2)
# 查看新特征数据
X_std_pca
'''
array([[ 9.19283683, 1.94858307],
[ 2.3878018 , -3.76817174],
[ 5.73389628, -1.0751738 ],
...,
[ 1.25617928, -1.90229671],
[ 10.37479406, 1.67201011],
[ -5.4752433 , -0.67063679]])
'''
```
## 使用 KMeans 聚类对观测分组
```py
# 加载库
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import pandas as pd
# 制作模拟特征矩阵
X, _ = make_blobs(n_samples = 50,
n_features = 2,
centers = 3,
random_state = 1)
# 创建 DataFrame
df = pd.DataFrame(X, columns=['feature_1','feature_2'])
# 创建 KMeans 聚类器
clusterer = KMeans(3, random_state=1)
# 拟合聚类器
clusterer.fit(X)
'''
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=3, n_init=10, n_jobs=1, precompute_distances='auto',
random_state=1, tol=0.0001, verbose=0)
'''
# 预测值
df['group'] = clusterer.predict(X)
# 前几个观测
df.head(5)
```
| | feature_1 | feature_2 | group |
| --- | --- | --- | --- |
| 0 | -9.877554 | -3.336145 | 0 |
| 1 | -7.287210 | -8.353986 | 2 |
| 2 | -6.943061 | -7.023744 | 2 |
| 3 | -7.440167 | -8.791959 | 2 |
| 4 | -6.641388 | -8.075888 | 2 |
# 为 LDA 选择最佳数量的成分
在 scikit-learn 中,LDA 是使用`LinearDiscriminantAnalysis`实现的,包含一个参数`n_components`,表示我们想要返回的特征数。 为了找出用于`n_components`的参数值(例如,要保留多少参数),我们可以利用一个事实,`explain_variance_ratio_`告诉我们每个输出特征的解释方差并且是有序数组。
具体来说,我们可以运行`Linear_iscriminantAnalysis`,将`n_components`设置为`None`来返回由每个特征成分的解释方差比,然后计算需要多少成分才能超过解释方差的阈值(通常为 0.95 或 0.99)。
```py
# 加载库
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 创建并运行 LDA
lda = LinearDiscriminantAnalysis(n_components=None)
X_lda = lda.fit(X, y)
# 创建解释方差比的数组
lda_var_ratios = lda.explained_variance_ratio_
# 创建函数
def select_n_components(var_ratio, goal_var: float) -> int:
# 设置目前为止的初始解释方差
total_variance = 0.0
# 设置初始特征数
n_components = 0
# 对于每个特征的解释方差
for explained_variance in var_ratio:
# 将解释方差添加到总体
total_variance += explained_variance
# 成分数加一
n_components += 1
# 如果我们达到了我们的解释方差目标
if total_variance >= goal_var:
# 结束循环
break
# 返回成分数量
return n_components
# 执行函数
select_n_components(lda_var_ratios, 0.95)
# 1
```
## 为 TSVD 选择最佳数量的成分
```py
# 加载库
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import TruncatedSVD
from scipy.sparse import csr_matrix
from sklearn import datasets
import numpy as np
# 加载数据
digits = datasets.load_digits()
# Standardize the feature matrix
X = StandardScaler().fit_transform(digits.data)
# 制作系数矩阵
X_sparse = csr_matrix(X)
# 创建并使用特征数减一运行 TSVD
tsvd = TruncatedSVD(n_components=X_sparse.shape[1]-1)
X_tsvd = tsvd.fit(X)
# 解释方差的列表
tsvd_var_ratios = tsvd.explained_variance_ratio_
# 创建函数
def select_n_components(var_ratio, goal_var: float) -> int:
# 设置目前为止的初始解释方差
total_variance = 0.0
# 设置初始特征数
n_components = 0
# 对于每个特征的解释方差
for explained_variance in var_ratio:
# 将解释方差添加到总体
total_variance += explained_variance
# 成分数加一
n_components += 1
# 如果我们达到了我们的解释方差目标
if total_variance >= goal_var:
# 结束循环
break
# 返回成分数量
return n_components
# 执行函数
select_n_components(tsvd_var_ratios, 0.95)
# 40
```
## 将 LDA 用于降维
```py
# 加载库
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 创建 LDA,它将数据降维到 1 个特征
lda = LinearDiscriminantAnalysis(n_components=1)
# 运行 LDA 并使用它转换特征
X_lda = lda.fit(X, y).transform(X)
# 打印特征数
print('Original number of features:', X.shape[1])
print('Reduced number of features:', X_lda.shape[1])
'''
Original number of features: 4
Reduced number of features: 1
'''
## 查看解释方差比
lda.explained_variance_ratio_
# array([ 0.99147248])
```
