# 十七、聚类
> 作者:[Chris Albon](https://chrisalbon.com/)
>
> 译者:[飞龙](https://github.com/wizardforcel)
>
> 协议:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
## 凝聚聚类

```py
# 加载库
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import AgglomerativeClustering
# 加载数据
iris = datasets.load_iris()
X = iris.data
# 标准化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
```
在 scikit-learn 中,`AgglomerativeClustering`使用`linkage`参数来确定合并策略,来最小化(1)合并簇的方差(`ward`),(2)来自簇对的观测点的距离均值(`average`) ,或(3)来自簇对的观测之间的最大距离(`complete`)。
其他两个参数很有用。 首先,`affinity`参数确定用于`linkage`的距离度量(`minkowski`,`euclidean`等)。 其次,`n_clusters`设置聚类算法将尝试查找的聚类数。 也就是说,簇被连续合并,直到只剩下`n_clusters`。
```py
# 创建聚类对象
clt = AgglomerativeClustering(linkage='complete',
affinity='euclidean',
n_clusters=3)
# 训练模型
model = clt.fit(X_std)
# 展示簇的成员
model.labels_
'''
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1,
1, 1, 1, 1, 0, 0, 0, 2, 0, 2, 0, 2, 0, 2, 2, 0, 2, 0, 0, 0, 0, 2, 2,
2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2, 0, 0, 0, 0, 2, 0, 2, 2, 0,
2, 2, 2, 0, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
'''
```
## DBSCAN 聚类

```py
# 加载库
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN
# 加载数据
iris = datasets.load_iris()
X = iris.data
# 标准化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
```
`DBSCAN`有三个要设置的主要参数:
* `eps`: 观测到被认为是邻居的另一个观测的最大距离
* `min_samples`: 小于上面的`eps`距离的最小观测数量
* `metric`: `eps`使用的距离度量。 例如,`minkowski`,`euclidean`等(请注意,如果使用 Minkowski 距离,参数`p`可用于设置 Minkowski 度量的指数)
如果我们在训练数据中查看簇,我们可以看到已经识别出两个簇,“0”和“1”,而异常观测被标记为“-1”。
```py
# 创建 DBSCAN 对象
clt = DBSCAN(n_jobs=-1)
# 训练模型
model = clt.fit(X_std)
```
## 评估聚类
```py
import numpy as np
from sklearn.metrics import silhouette_score
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# 生成特征矩阵
X, _ = make_blobs(n_samples = 1000,
n_features = 10,
centers = 2,
cluster_std = 0.5,
shuffle = True,
random_state = 1)
# 使用 k-means 来对数据聚类
model = KMeans(n_clusters=2, random_state=1).fit(X)
# 获取预测的类别
y_hat = model.labels_
```
正式地,第 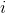 个观测的轮廓系数是:
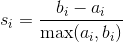
其中 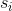 是观测 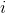 的轮廓系数,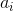 是 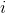 和同类的所有观测值之间的平均距离,而 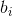 是 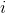 和不同类的所有观测的平均距离的最小值。`silhouette_score`返回的值是所有观测值的平均轮廓系数。 轮廓系数介于 -1 和 1 之间,其中 1 表示密集,分离良好的聚类。
```py
# 评估模型
silhouette_score(X, y_hat)
# 0.89162655640721422
```
## 均值移动聚类

```py
# 加载库
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import MeanShift
# 加载数据
iris = datasets.load_iris()
X = iris.data
# 标准化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
```
`MeanShift`有两个我们应该注意的重要参数。 首先,`bandwidth`设置区域(即观测核)半径,用于确定移动方向。 在我们的比喻中,带宽是一个人可以在雾中看到的距离。 我们可以手动设置此参数,但默认情况下会自动估算合理的带宽(计算成本会显着增加)。 其次,有时在均值移动中,观测核中没有其他观测结果。 也就是说,我们足球上的一个人看不到任何其它人。 默认情况下,`MeanShift`将所有这些“孤例”观测值分配给最近观测核。 但是,如果我们想要留出这些孤例,我们可以设置`cluster_all = False`,其中孤例观测标签为 -1。
```py
# 创建 MeanShift 对象
clt = MeanShift(n_jobs=-1)
# 训练模型
model = clt.fit(X_std)
```
## 小批量 KMeans 聚类
小批量 k-means 的工作方式与上一个方案中讨论的 k-means 算法类似。 没有太多细节,不同之处在于,在小批量 k-means中,计算成本最高的步骤仅在随机的观测样本上进行,而不是所有观测。 这种方法可以显着减少算法发现收敛(即适合数据)所需的时间,而质量成本很低。
```py
# 加载库
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import MiniBatchKMeans
# 加载数据
iris = datasets.load_iris()
X = iris.data
# 标准化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
```
`MiniBatchKMeans`与`KMeans`的工作方式类似,有一个显着性差异:`batch_size`参数。 `batch_size`控制每批中随机选择的观测数。 批量越大,训练过程的计算成本就越高。
```py
# 创建 KMeans 对象
clustering = MiniBatchKMeans(n_clusters=3, random_state=0, batch_size=100)
# 训练模型
model = clustering.fit(X_std)
```
## KMeans 聚类

```py
# 加载库
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
# 加载数据
iris = datasets.load_iris()
X = iris.data
# 标准化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 创建 KMeans 对象
clt = KMeans(n_clusters=3, random_state=0, n_jobs=-1)
# 训练模型
model = clt.fit(X_std)
# 查看预测类别
model.labels_
'''
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 0, 0, 0, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2,
2, 0, 2, 2, 2, 2, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 0, 0, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 2, 2,
0, 0, 0, 0, 2, 0, 2, 0, 2, 0, 0, 2, 0, 0, 0, 0, 0, 0, 2, 2, 0, 0, 0,
2, 0, 0, 0, 2, 0, 0, 0, 2, 0, 0, 2], dtype=int32)
'''
# 创建新的观测
new_observation = [[0.8, 0.8, 0.8, 0.8]]
# 预测观测的类别
model.predict(new_observation)
# array([0], dtype=int32)
# 查看簇中心
model.cluster_centers_
'''
array([[ 1.13597027, 0.09659843, 0.996271 , 1.01717187],
[-1.01457897, 0.84230679, -1.30487835, -1.25512862],
[-0.05021989, -0.88029181, 0.34753171, 0.28206327]])
'''
```
