# 7 -- The VC Dimension
前几节课着重介绍了机器能够学习的条件并做了详细的推导和解释。机器能够学习必须满足两个条件:
* **假设空间H的Size M是有限的,即当N足够大的时候,那么对于假设空间中任意一个假设g,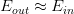**。
* **利用算法A从假设空间H中,挑选一个g,使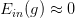,则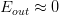**。
这两个条件,正好对应着test和trian两个过程。train的目的是使损失期望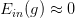;test的目的是使将算法用到新的样本时的损失期望也尽可能小,即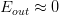。
正因为如此,上次课引入了break point,并推导出只要break point存在,则M有上界,一定存在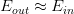。
本次笔记主要介绍VC Dimension的概念。同时也是总结VC Dimension与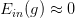,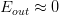,Model Complexity Penalty(下面会讲到)的关系。
### **一、Definition of VC Dimension**
首先,我们知道如果一个假设空间H有break point k,那么它的成长函数是有界的,它的上界称为Bound function。根据数学归纳法,Bound function也是有界的,且上界为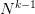。从下面的表格可以看出,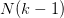比B(N,k)松弛很多。

则根据上一节课的推导,VC bound就可以转换为:
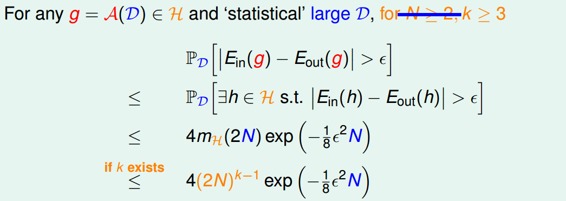
这样,不等式只与k和N相关了,一般情况下样本N足够大,所以我们只考虑k值。有如下结论:
* **若假设空间H有break point k,且N足够大,则根据VC bound理论,算法有良好的泛化能力**
* **在假设空间中选择一个矩g,使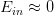,则其在全集数据中的错误率会较低**

下面介绍一个新的名词:VC Dimension。VC Dimension就是某假设集H能够shatter的最多inputs的个数,即最大完全正确的分类能力。(注意,只要存在一种分布的inputs能够正确分类也满足)。
shatter的英文意思是“粉碎”,也就是说对于inputs的所有情况都能列举出来。例如对N个输入,如果能够将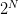种情况都列出来,则称该N个输入能够被假设集H shatter。
根据之前break point的定义:假设集不能被shatter任何分布类型的inputs的最少个数。则VC Dimension等于break point的个数减一。

现在,我们回顾一下之前介绍的四种例子,它们对应的VC Dimension是多少:
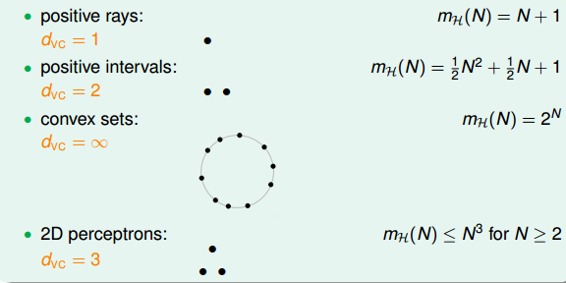
用代替k,那么VC bound的问题也就转换为与和N相关了。同时,如果一个假设集H的确定了,则就能满足机器能够学习的第一个条件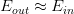,与算法、样本数据分布和目标函数都没有关系。
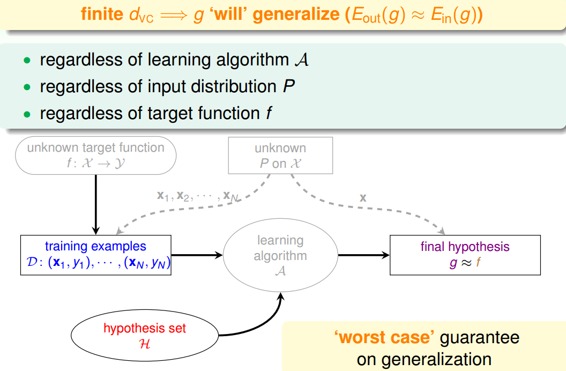
### **二、VC Dimension of Perceptrons**
回顾一下我们之前介绍的2D下的PLA算法,已知Perceptrons的k=4,即。根据VC Bound理论,当N足够大的时候,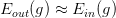。如果找到一个g,使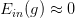,那么就能证明PLA是可以学习的。
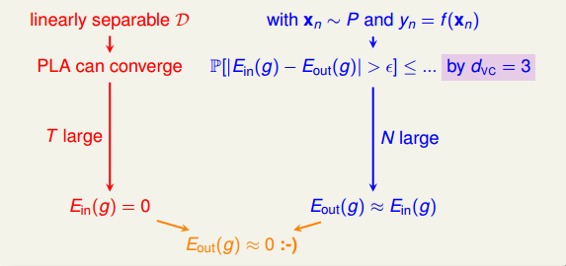
这是在2D情况下,那如果是多维的Perceptron,它对应的又等于多少呢?
已知在1D Perceptron,,在2D Perceptrons,,那么我们有如下假设:,其中d为维数。
要证明的话,只需分两步证明:
* 
* 
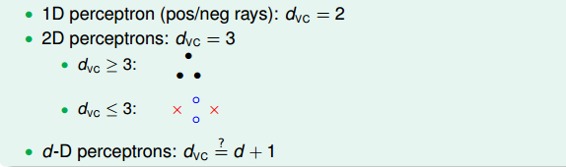
首先证明第一个不等式:。
在d维里,我们只要找到某一类的d+1个inputs可以被shatter的话,那么必然得到。所以,我们有意构造一个d维的矩阵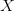能够被shatter就行。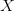是d维的,有d+1个inputs,每个inputs加上第零个维度的常数项1,得到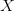的矩阵:
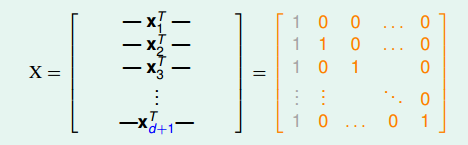
矩阵中,每一行代表一个inputs,每个inputs是d+1维的,共有d+1个inputs。这里构造的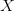很明显是可逆的。shatter的本质是假设空间H对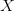的所有情况的判断都是对的,即总能找到权重W,满足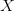,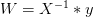。由于这里我们构造的矩阵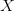的逆矩阵存在,那么d维的所有inputs都能被shatter,也就证明了第一个不等式。
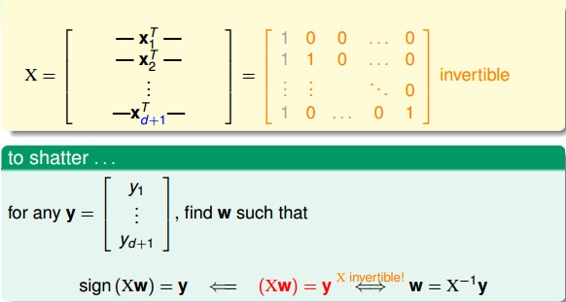
然后证明第二个不等式:。
在d维里,如果对于任何的d+2个inputs,一定不能被shatter,则不等式成立。我们构造一个任意的矩阵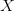,其包含d+2个inputs,该矩阵有d+1列,d+2行。这d+2个向量的某一列一定可以被另外d+1个向量线性表示,例如对于向量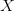,可表示为:
其中,假设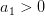,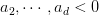.
那么如果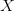是正类,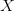均为负类,则存在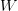,得到如下表达式:
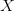<font color="#0000ff">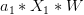</font>+<font color="#ff0000">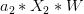</font>++<font color="#ff0000">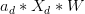</font>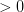
因为其中蓝色项大于0,代表正类;红色项小于0,代表负类。所有对于这种情况,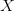一定是正类,无法得到负类的情况。也就是说,d+2个inputs无法被shatter。证明完毕!

综上证明可得。
### **三、Physical Intuition VC Dimension**

上节公式中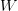又名features,即自由度。自由度是可以任意调节的,如同上图中的旋钮一样,可以调节。VC Dimension代表了假设空间的分类能力,即反映了H的自由度,产生dichotomy的数量,也就等于features的个数,但也不是绝对的。

例如,对2D Perceptrons,线性分类,,则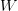,也就是说只要3个features就可以进行学习,自由度为3。
介绍到这,我们发现M与是成正比的,从而得到如下结论:

### **四、Interpreting VC Dimension**
下面,我们将更深入地探讨VC Dimension的意义。首先,把VC Bound重新写到这里:

根据之前的泛化不等式,如果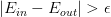,即出现bad坏的情况的概率最大不超过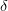。那么反过来,对于good好的情况发生的概率最小为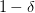,则对上述不等式进行重新推导:

表现了假设空间H的泛化能力,越小,泛化能力越大。

至此,已经推导出泛化误差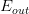的边界,因为我们更关心其上界(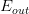可能的最大值),即:
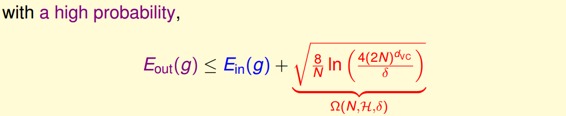
上述不等式的右边第二项称为模型复杂度,其模型复杂度与样本数量N、假设空间H()、有关。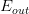由共同决定。下面绘出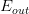、model complexity、随变化的关系:

通过该图可以得出如下结论:
* **越大,越小,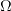越大(复杂)**。
* **越小,越大,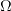越小(简单)**。
* **随着增大,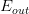会先减小再增大**。
所以,为了得到最小的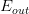,不能一味地增大以减小,因为太小的时候,模型复杂度会增加,造成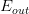变大。也就是说,选择合适的,选择的features个数要合适。
下面介绍一个概念:样本复杂度(Sample Complexity)。如果选定,样本数据D选择多少合适呢?通过下面一个例子可以帮助我们理解:

通过计算得到N=29300,刚好满足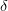的条件。N大约是的10000倍。这个数值太大了,实际中往往不需要这么多的样本数量,大概只需要的10倍就够了。N的理论值之所以这么大是因为VC Bound 过于宽松了,我们得到的是一个比实际大得多的上界。

值得一提的是,VC Bound是比较宽松的,而如何收紧它却不是那么容易,这也是机器学习的一大难题。但是,令人欣慰的一点是,VC Bound基本上对所有模型的宽松程度是基本一致的,所以,不同模型之间还是可以横向比较。从而,VC Bound宽松对机器学习的可行性还是没有太大影响。
### **五、总结**
本节课主要介绍了VC Dimension的概念就是最大的non-break point。然后,我们得到了Perceptrons在d维度下的VC Dimension是d+1。接着,我们在物理意义上,将与自由度联系起来。最终得出结论不能过大也不能过小。选取合适的值,才能让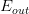足够小,使假设空间H具有良好的泛化能力。
**_注明:_**
文章中所有的图片均来自台湾大学林轩田《机器学习基石》课程
- 台湾大学林轩田机器学习笔记
- 机器学习基石
- 1 -- The Learning Problem
- 2 -- Learning to Answer Yes/No
- 3 -- Types of Learning
- 4 -- Feasibility of Learning
- 5 -- Training versus Testing
- 6 -- Theory of Generalization
- 7 -- The VC Dimension
- 8 -- Noise and Error
- 9 -- Linear Regression
- 10 -- Logistic Regression
- 11 -- Linear Models for Classification
- 12 -- Nonlinear Transformation
- 13 -- Hazard of Overfitting
- 14 -- Regularization
- 15 -- Validation
- 16 -- Three Learning Principles
- 机器学习技法
- 1 -- Linear Support Vector Machine
- 2 -- Dual Support Vector Machine
- 3 -- Kernel Support Vector Machine
- 4 -- Soft-Margin Support Vector Machine
- 5 -- Kernel Logistic Regression
- 6 -- Support Vector Regression
- 7 -- Blending and Bagging
- 8 -- Adaptive Boosting
- 9 -- Decision Tree
- 10 -- Random Forest
- 11 -- Gradient Boosted Decision Tree
- 12 -- Neural Network
- 13 -- Deep Learning
- 14 -- Radial Basis Function Network
- 15 -- Matrix Factorization
- 16(完结) -- Finale
