# 10 -- Logistic Regression
上一节课,我们介绍了Linear Regression线性回归,以及用平方错误来寻找最佳的权重向量w,获得最好的线性预测。本节课将介绍Logistic Regression逻辑回归问题。
### **一、Logistic Regression Problem**
一个心脏病预测的问题:根据患者的年龄、血压、体重等信息,来预测患者是否会有心脏病。很明显这是一个二分类问题,其输出y只有{-1,1}两种情况。
二元分类,一般情况下,理想的目标函数f(x)>0.5,则判断为正类1;若f(x)<0.5,则判断为负类-1。
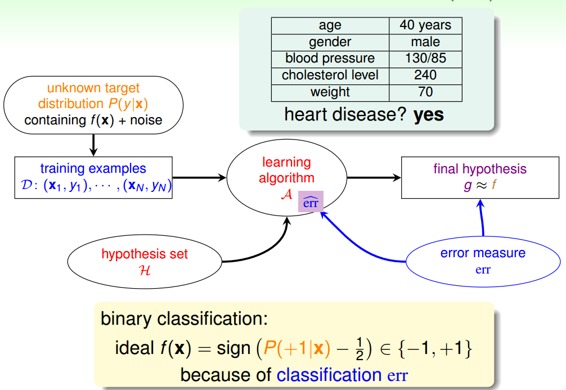
但是,如果我们想知道的不是患者有没有心脏病,而是到底患者有多大的几率是心脏病。这表示,我们更关心的是目标函数的值(分布在0,1之间),表示是正类的概率(正类表示是心脏病)。这跟我们原来讨论的二分类问题不太一样,我们把这个问题称为软性二分类问题(’soft’ binary classification)。这个值越接近1,表示正类的可能性越大;越接近0,表示负类的可能性越大。

对于软性二分类问题,理想的数据是分布在[0,1]之间的具体值,但是实际中的数据只可能是0或者1,我们可以把实际中的数据看成是理想数据加上了噪声的影响。
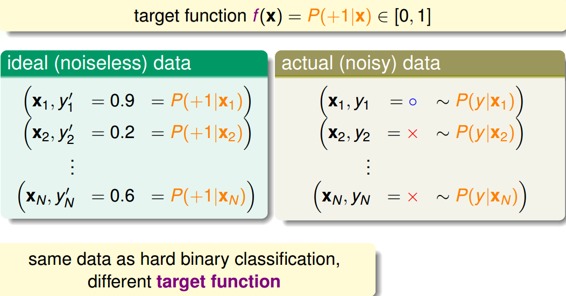
如果目标函数是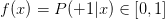的话,我们如何找到一个好的Hypothesis跟这个目标函数很接近呢?
首先,根据我们之前的做法,对所有的特征值进行加权处理。计算的结果s,我们称之为’risk score’:

但是特征加权和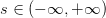,如何将s值限定在[0,1]之间呢?一个方法是使用sigmoid Function,记为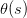。那么我们的目标就是找到一个hypothesis: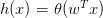。

Sigmoid Function函数记为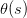,满足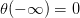,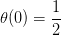,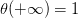。这个函数是平滑的、单调的S型函数。则对于逻辑回归问题,hypothesis就是这样的形式:
那我们的目标就是求出这个预测函数h(x),使它接近目标函数f(x)。
### **二、Logistic Regression Error**
现在我们将Logistic Regression与之前讲的Linear Classification、Linear Regression做个比较:
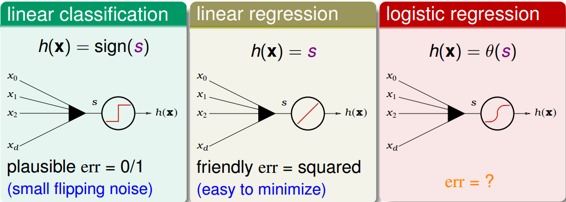
这三个线性模型都会用到线性scoring function 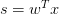。linear classification的误差使用的是0/1 err;linear regression的误差使用的是squared err。那么logistic regression的误差该如何定义呢?
先介绍一下“似然性”的概念。目标函数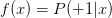,如果我们找到了hypothesis很接近target function。也就是说,在所有的Hypothesis集合中找到一个hypothesis与target function最接近,能产生同样的数据集D,包含y输出label,则称这个hypothesis是最大似然likelihood。

logistic function: 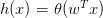满足一个性质: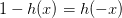。那么,似然性h:
因为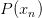对所有的h来说,都是一样的,所以我们可以忽略它。那么我们可以得到logistic h正比于所有的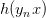乘积。我们的目标就是让乘积值最大化。

如果将w代入的话:
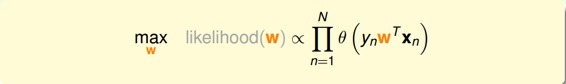
为了把连乘问题简化计算,我们可以引入ln操作,让连乘转化为连加:
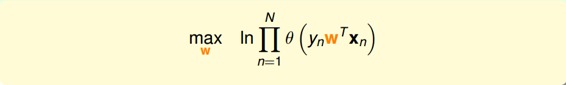
接着,我们将maximize问题转化为minimize问题,添加一个负号就行,并引入平均数操作:
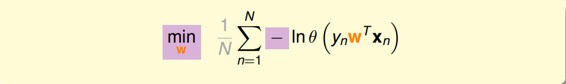
将logistic function的表达式带入,那么minimize问题就会转化为如下形式:
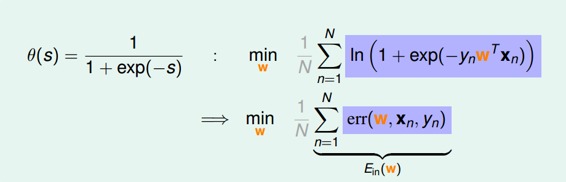
至此,我们得到了logistic regression的err function,称之为cross-entropy error交叉熵误差:

### **三、Gradient of Logistic Regression Error**
我们已经推导了的表达式,那接下来的问题就是如何找到合适的向量w,让最小。
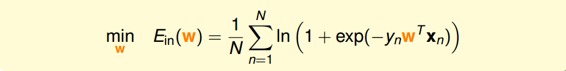
Logistic Regression的是连续、可微、二次可微的凸曲线(开口向上),根据之前Linear Regression的思路,我们只要计算的梯度为零时的w,即为最优解。

对计算梯度,学过微积分的都应该很容易计算出来:
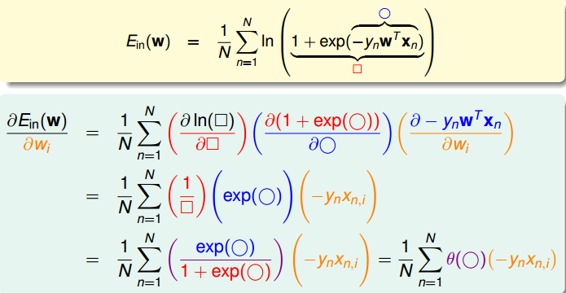
最终得到的梯度表达式为:
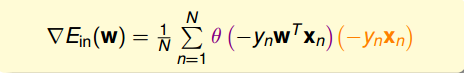
为了计算最小值,我们就要找到让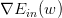等于0的位置。
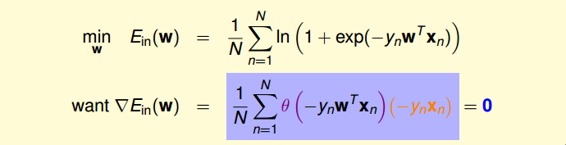
上式可以看成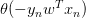是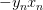的线性加权。要求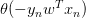与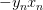的线性加权和为0,那么一种情况是线性可分,如果所有的权重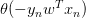为0,那就能保证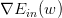为0。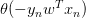是sigmoid function,根据其特性,只要让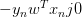,即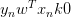。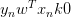表示对于所有的点,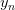与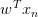都是同号的,这表示数据集D必须是全部线性可分的才能成立。
然而,保证所有的权重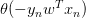为0是不太现实的,总有不等于0的时候,那么另一种常见的情况是非线性可分,只能通过使加权和为零,来求解w。这种情况没有closed-form解,与Linear Regression不同,只能用迭代方法求解。

之前所说的Linear Regression有closed-form解,可以说是“一步登天”的;但是PLA算法是一步一步修正迭代进行的,每次对错误点进行修正,不断更新w值。PLA的迭代优化过程表示如下:

w每次更新包含两个内容:一个是每次更新的方向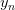,用表示,另一个是每次更新的步长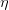。参数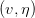和终止条件决定了我们的迭代优化算法。

### **四、Gradient Descent**
根据上一小节PLA的思想,迭代优化让每次w都有更新:
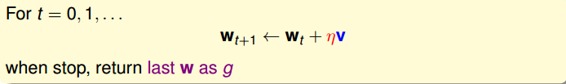
我们把曲线看做是一个山谷的话,要求最小,即可比作下山的过程。整个下山过程由两个因素影响:一个是下山的单位方向;另外一个是下山的步长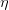。

利用微分思想和线性近似,假设每次下山我们只前进一小步,即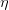很小,那么根据泰勒Taylor一阶展开,可以得到:
关于Taylor展开的介绍,可参考我另一篇博客:
[多元函数的泰勒(Taylor)展开式](http://blog.csdn.net/red_stone1/article/details/70260070)
迭代的目的是让越来越小,即让。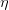是标量,因为如果两个向量方向相反的话,那么他们的内积最小(为负),也就是说如果方向与梯度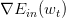反向的话,那么就能保证每次迭代都成立。则,我们令下降方向为:
是单位向量,每次都是沿着梯度的反方向走,这种方法称为梯度下降(gradient descent)算法。那么每次迭代公式就可以写成:
下面讨论一下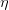的大小对迭代优化的影响: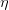如果太小的话,那么下降的速度就会很慢;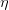如果太大的话,那么之前利用Taylor展开的方法就不准了,造成下降很不稳定,甚至会上升。因此,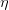应该选择合适的值,一种方法是在梯度较小的时候,选择小的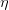,梯度较大的时候,选择大的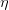,即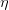正比于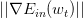。这样保证了能够快速、稳定地得到最小值。
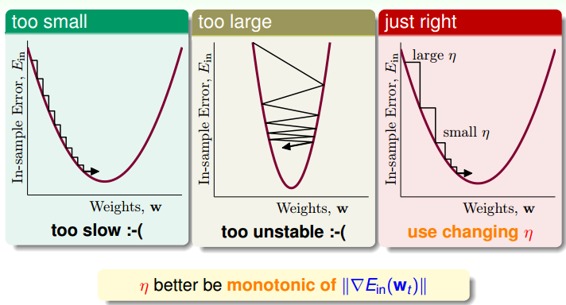
对学习速率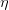做个更修正,梯度下降算法的迭代公式可以写成:
其中:
总结一下基于梯度下降的Logistic Regression算法步骤如下:
* **初始化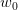**
* **计算梯度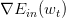**
* **迭代跟新**
* **满足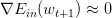或者达到迭代次数,迭代结束**
### **五、总结**
我们今天介绍了Logistic Regression。首先,从逻辑回归的问题出发,将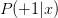作为目标函数,将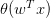作为hypothesis。接着,我们定义了logistic regression的err function,称之为cross-entropy error交叉熵误差。然后,我们计算logistic regression error的梯度,最后,通过梯度下降算法,计算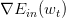时对应的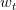值。
**_注明:_**
文章中所有的图片均来自台湾大学林轩田《机器学习基石》课程
- 台湾大学林轩田机器学习笔记
- 机器学习基石
- 1 -- The Learning Problem
- 2 -- Learning to Answer Yes/No
- 3 -- Types of Learning
- 4 -- Feasibility of Learning
- 5 -- Training versus Testing
- 6 -- Theory of Generalization
- 7 -- The VC Dimension
- 8 -- Noise and Error
- 9 -- Linear Regression
- 10 -- Logistic Regression
- 11 -- Linear Models for Classification
- 12 -- Nonlinear Transformation
- 13 -- Hazard of Overfitting
- 14 -- Regularization
- 15 -- Validation
- 16 -- Three Learning Principles
- 机器学习技法
- 1 -- Linear Support Vector Machine
- 2 -- Dual Support Vector Machine
- 3 -- Kernel Support Vector Machine
- 4 -- Soft-Margin Support Vector Machine
- 5 -- Kernel Logistic Regression
- 6 -- Support Vector Regression
- 7 -- Blending and Bagging
- 8 -- Adaptive Boosting
- 9 -- Decision Tree
- 10 -- Random Forest
- 11 -- Gradient Boosted Decision Tree
- 12 -- Neural Network
- 13 -- Deep Learning
- 14 -- Radial Basis Function Network
- 15 -- Matrix Factorization
- 16(完结) -- Finale
