# 15 -- Matrix Factorization 上节课我们主要介绍了Radial Basis Function Network。它的原理就是基于距离相似性（distance-based similarities）的线性组合（linear aggregation）。我们使用k-Means clustering算法找出具有代表性的k个中心点，然后再计算与这些中心点的distance similarity，最后应用到RBF Network中去。 ### **LinearNetwork Hypothesis** 回顾一下，我们在机器学习基石课程的第一节课就提到过，机器学习的目的就是让机器从数据data中学习到某种能力skill。我们之前举过一个典型的推荐系统的例子。就是说，假如我们手上有许多不同用户对不同电影的排名rank，通过机器学习，训练一个模型，能够对用户没有看过的某部电影进行排名预测。  一个典型的电影推荐系统的例子是2006年Netflix举办的一次比赛。数据包含了480189个用户和17770部电影，总共1亿多个排名信息。该推荐系统模型中，我们用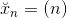表示第n个用户，这是一个抽象的特征，常常使用数字编号来代替具体哪个用户。输出方面，我们使用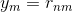表示第n个用户对第m部电影的排名数值。  下面我们来进一步看看这些抽象的特征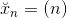，是用户的ID，通常用数字表示。例如1126,5566,6211等。这些编号并没有数值大小上的意义，只是一种ID标识而已。这类特征被称为类别特征（categorical features）。常见的categorical features包括：IDs，blood type，programming languages等等。而许多机器学习模型中使用的大部分都是数值特征（numerical features）。例如linear models，NNet模型等。但决策树（decision tree）是个例外，它可以使用categorical features。所以说，如果要建立一个类似推荐系统的机器学习模型，就要把用户ID这种categorical features转换为numerical features。这种特征转换其实就是训练模型之前一个编码（encoding）的过程。  一种最简单的encoding方式就是binary vector encoding。也就是说，如果输入样本有N个，就构造一个维度为N的向量。第n个样本对应向量上第n个元素为1，其它元素都是0。下图就是一个binary vector encoding的例子。  经过encoding之后，输入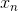是N维的binary vector，表示第n个用户。输出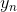是M维的向量，表示该用户对M部电影的排名数值大小。注意，用户不一定对所有M部电影都作过评价，未评价的恰恰是我们要预测的（下图中问号？表示未评价的电影）。  总共有N个用户，M部电影。对于这样的数据，我们需要掌握每个用户对不同电影的喜爱程度及排名。这其实就是一个特征提取（feature extraction）的过程，提取出每个用户喜爱的电影风格及每部电影属于哪种风格，从而建立这样的推荐系统模型。可供选择使用的方法和模型很多，这里，我们使用的是NNet模型。NNet模型中的网络结构是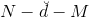型，其中N是输入层样本个数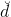，是隐藏层神经元个数，M是输出层电影个数。该NNet为了简化计算，忽略了常数项。当然可以选择加上常数项，得到较复杂一些的模型。顺便提一下，这个结构跟我们之前介绍的autoencoder非常类似，都是只有一个隐藏层。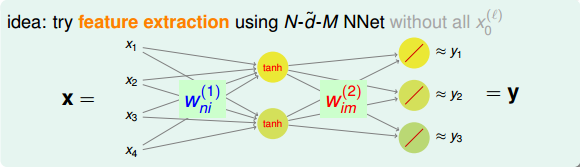  说到这里，有一个问题，就是上图NNet中隐藏层的tanh函数是否一定需要呢？答案是不需要。因为输入向量x是经过encoding得到的，其中大部分元素为0，只有一个元素为1。那么，只有一个元素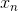与相应权重的乘积进入到隐藏层。由于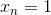，则相当于只有一个权重值进入到tanh函数进行运算。从效果上来说，tanh(x)与x是无差别的，只是单纯经过一个函数的计算，并不影响最终的结果，修改权重值即可得到同样的效果。因此，我们把隐藏层的tanh函数替换成一个线性函数y=x，得到下图所示的结构。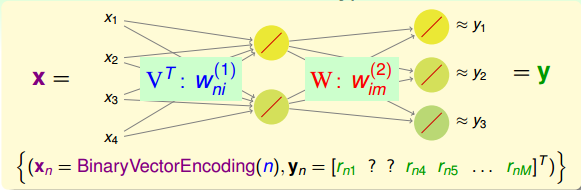  由于中间隐藏层的转换函数是线性的，我们把这种结构称为Linear Network（与linear autoencoder比较相似）。看一下上图这个网络结构，输入层到隐藏层的权重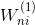维度是Nx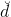，用向量表示。隐藏层到输出层的权重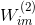维度是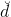xM，用矩阵W表示。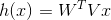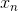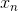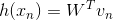把权重由矩阵表示之后，Linear Network的hypothesis 可表示为：  如果是单个用户，由于X向量中只有元素为1，其它均为0，则对应矩阵V只有第n列向量是有效的，其输出hypothesis为：   ### **Basic Matrix Factorization** 刚刚我们已经介绍了linear network的模型和hypothesis。其中Vx可以看作是对用户x的一种特征转换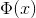。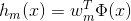对于单部电影，其预测的排名可表示为：   推导完linear network模型之后，对于每组样本数据（即第n个用户第m部电影），我们希望预测的排名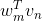与实际样本排名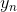尽可能接近。所有样本综合起来，我们使用squared error measure的方式来定义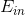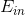，的表达式如下所示：  上式中，灰色的部分是常数，并不影响最小化求解，所以可以忽略。接下来，我们就要求出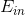最小化时对应的V和W解。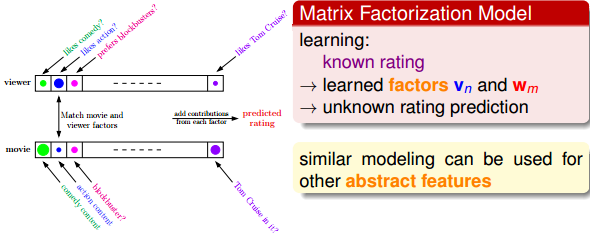 我们的目标是让真实排名与预测排名尽可能一致，即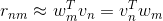。把这种近似关系写成矩阵的形式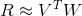：。矩阵R表示所有不同用户不同电影的排名情况，维度是NxM。这种用矩阵的方式进行处理的方法叫做Matrix Factorization。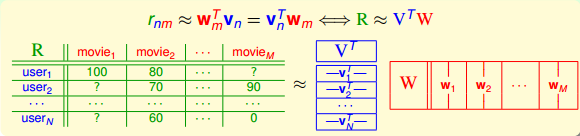  上面的表格说明了我们希望将实际排名情况R分解成两个矩阵（V和W）的乘积形式。V的维度是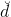xN的，N是用户个数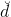，可以是影片类型，例如（喜剧片，爱情片，悬疑片，动作片，…）。根据用户喜欢的类型不同，赋予不同的权重。W的维度是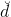xM，M是电影数目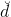，同样是影片类型，该部电影属于哪一类型就在那个类型上占比较大的权重。当然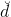，维特征不一定就是影片类型，还可以是其它特征，例如明显阵容、年代等等。  那么，Matrix Factorization的目标就是最小化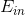函数。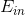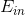表达式如下所示：  中包含了两组待优化的参数，分别是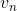和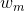。我们可以借鉴上节课中k-Means的做法，将其中第一个参数固定，优化第二个参数，然后再固定第二个参数，优化第一个参数，一步一步进行优化。 当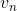固定的时候，只需要对每部电影做linear regression即可，优化得到每部电影的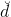维特征值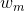。 当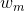固定的时候，因为V和W结构上是对称的，同样只需要对每个用户做linear regression即可，优化得到每个用户对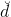维电影特征的喜爱程度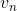。  这种算法叫做alternating least squares algorithm。它的处理思想与k-Means算法相同，其算法流程图如下所示：  alternating least squares algorithm有两点需要注意。第一是initialize问题，通常会随机选取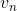和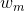。第二是converge问题，由于每次迭代更新都能减小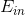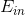，会趋向于0，则保证了算法的收敛性。  在上面的分析中，我们提过Matrix Factorization与Linear Autoencoder的相似性，下图列出了二者之间的比较。  Matrix Factorization与Linear Autoencoder有很强的相似性，都可以从原始资料汇总提取有用的特征。其实，linear autoencoder可以看成是matrix factorization的一种特殊形式。 ### **Stochastic Gradient Descent** 我们刚刚介绍了alternating least squares algorithm来解决Matrix Factorization的问题。这部分我们将讨论使用Stochastic Gradient Descent方法来进行求解。之前的alternating least squares algorithm中，我们考虑了所有用户、所有电影。现在使用SGD，随机选取一笔资料，然后只在与这笔资料有关的error function上使用梯度下降算法。使用SGD的好处是每次迭代只要处理一笔资料，效率很高；而且程序简单，容易实现；最后，很容易扩展到其它的error function来实现。  对于每笔资料，它的error function可表示为：  上式中的err是squared error function，仅与第n个用户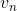，第m部电影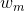有关。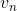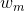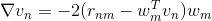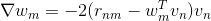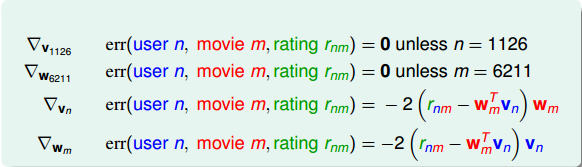其对和的偏微分结果为：    很明显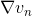，和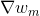都由两项乘积构成。（忽略常数因子2）。第一项都是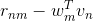，即余数residual。我们在之前介绍的GBDT算法中也介绍过余数这个概念。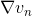的第二项是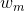，而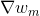的第二项是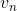。二者在结构上是对称的。 计算完任意一个样本点的SGD后，就可以构建Matrix Factorization的算法流程。SGD for Matrix Factorization的算法流程如下所示：  在实际应用中，由于SGD算法简单高效，Matrix Factorization大多采用这种算法。 介绍完SGD for Matrix Factorization之后，我们来看一个实际的应用例子。问题大致是这样的：根据现在有的样本资料，预测未来的趋势和结果。显然，这是一个与时间先后有关的预测模型。比如说一个用户三年前喜欢的电影可能现在就不喜欢了。所以在使用SGD选取样本点的时候有一个技巧，就是最后T次迭代，尽量选择时间上靠后的样本放入到SGD算法中。这样最后的模型受这些时间上靠后的样本点影响比较大，也相对来说比较准确，对未来的预测会比较准。  所以，在实际应用中，我们除了使用常规的机器学习算法外，还需要根据样本数据和问题的实际情况来修改我们的算法，让模型更加切合实际，更加准确。我们要学会灵活运用各种机器学习算法，而不能只是照搬。 ### **Summary of Extraction Models** 从第12节课开始到现在，我们总共用了四节课的时间来介绍Extraction Models。虽然我们没有给出Extraction Models明确的定义，但是它主要的功能就是特征提取和特征转换，将原始数据更好地用隐藏层的一些节点表征出来，最后使用线性模型将所有节点aggregation。这种方法使我们能够更清晰地抓住数据的本质，从而建立最佳的机器学习模型。 下图所示的就是我们介绍过的所有Extraction Models，除了这四节课讲的内容之外，还包括之前介绍的Adaptive/Gradient Boosting模型。因为之前笔记中都详细介绍过，这里就不再一一总结了。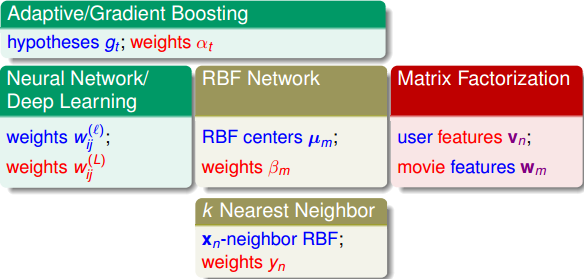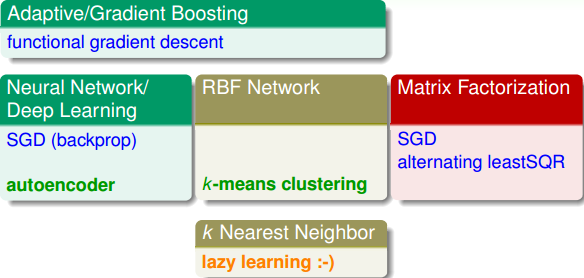  除了各种Extraction Models之外，我们这四节课还介绍了不同的Extraction Techniques。下图所示的是对应于不同的Extraction Models的Extraction Techniques。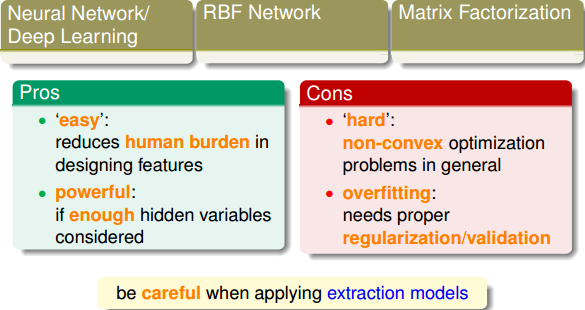  最后，总结一下这些Extraction Models有什么样的优点和缺点。从优点上来说： * **easy：机器自己完成特征提取，减少人类工作量** * **powerful：能够处理非常复杂的问题和特征提取** 另一方面，从缺点上来说： * **hard：通常遇到non-convex的优化问题，求解较困难，容易得到局部最优解而非全局最优解** * **overfitting：模型复杂，容易造成过拟合，需要进行正则化处理** 所以说，Extraction Models是一个非常强大的机器学习工具，但是使用的时候也要小心处理各种可能存在的问题。  ### **总结** 本节课主要介绍了Matrix Factorization。从电影推荐系统模型出发，首先，我们介绍了Linear Network。它从用户ID编码后的向量中提取出有用的特征，这是典型的feature extraction。然后，我们介绍了基本的Matrix Factorization算法，即alternating least squares，不断地在用户和电影之间交互地做linear regression进行优化。为了简化计算，提高运算速度，也可以使用SGD来实现。事实证明，SGD更加高效和简单。同时，我们可以根据具体的问题和需求，对固有算法进行一些简单的调整，来获得更好的效果。最后，我们对已经介绍的所有Extraction Models做个简单的总结。Extraction Models在实际应用中是个非常强大的工具，但是也要避免出现过拟合等问题。 **_注明：_** 文章中所有的图片均来自台湾大学林轩田《机器学习技法》课程