## 最长回文子串
### 题目描述
给定一个字符串,求它的最长回文子串的长度。
### 分析与解法
最容易想到的办法是枚举所有的子串,分别判断其是否为回文。这个思路初看起来是正确的,但却做了很多无用功,如果一个长的子串包含另一个短一些的子串,那么对子串的回文判断其实是不需要的。
#### 解法一
那么如何高效的进行判断呢?我们想想,如果一段字符串是回文,那么以某个字符为中心的前缀和后缀都是相同的,例如以一段回文串“aba”为例,以b为中心,它的前缀和后缀都是相同的,都是a。
那么,我们是否可以可以枚举中心位置,然后再在该位置上用扩展法,记录并更新得到的最长的回文长度呢?答案是肯定的,参考代码如下:
```cpp
int LongestPalindrome(const char *s, int n)
{
int i, j, max,c;
if (s == 0 || n < 1)
return 0;
max = 0;
for (i = 0; i < n; ++i) { // i is the middle point of the palindrome
for (j = 0; (i - j >= 0) && (i + j < n); ++j){ // if the length of the palindrome is odd
if (s[i - j] != s[i + j])
break;
c = j * 2 + 1;
}
if (c > max)
max = c;
for (j = 0; (i - j >= 0) && (i + j + 1 < n); ++j){ // for the even case
if (s[i - j] != s[i + j + 1])
break;
c = j * 2 + 2;
}
if (c > max)
max = c;
}
return max;
}
```
代码稍微难懂一点的地方就是内层的两个 for 循环,它们分别对于以 i 为中心的,长度为奇数和偶数的两种情况,整个代码遍历中心位置 i 并以之扩展,找出最长的回文。
#### 解法二、O(N)解法
在上文的解法一:枚举中心位置中,我们需要特别考虑字符串的长度是奇数还是偶数,所以导致我们在编写代码实现的时候要把奇数和偶数的情况分开编写,是否有一种方法,可以不用管长度是奇数还是偶数,而统一处理呢?比如是否能把所有的情况全部转换为奇数处理?
答案还是肯定的。这就是下面我们将要看到的Manacher算法,且这个算法求最长回文子串的时间复杂度是线性O(N)的。
首先通过在每个字符的两边都插入一个特殊的符号,将所有可能的奇数或偶数长度的回文子串都转换成了奇数长度。比如 abba 变成 #a#b#b#a#, aba变成 #a#b#a#。
此外,为了进一步减少编码的复杂度,可以在字符串的开始加入另一个特殊字符,这样就不用特殊处理越界问题,比如$#a#b#a#。
以字符串12212321为例,插入#和$这两个特殊符号,变成了 S[] = "$#1#2#2#1#2#3#2#1#",然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左或向右扩张的长度(包括S[i])。
比如S和P的对应关系:
- S # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #
- P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
可以看出,P[i]-1正好是原字符串中最长回文串的总长度,为5。
接下来怎么计算P[i]呢?Manacher算法增加两个辅助变量id和mx,其中id表示最大回文子串中心的位置,mx则为id+P[id],也就是最大回文子串的边界。得到一个很重要的结论:
- 如果mx > i,那么P[i] >= Min(P[2 * id - i], mx - i)
C代码如下:
```c
//mx > i,那么P[i] >= MIN(P[2 * id - i], mx - i)
//故谁小取谁
if (mx - i > P[2*id - i])
P[i] = P[2*id - i];
else //mx-i <= P[2*id - i]
P[i] = mx - i;
```
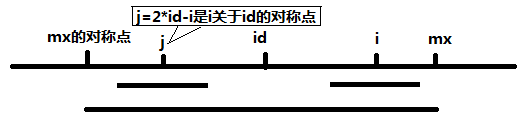
下面,令j = 2*id - i,也就是说j是i关于id的对称点。
当 mx - i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于i和j对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有P[i] = P[j];
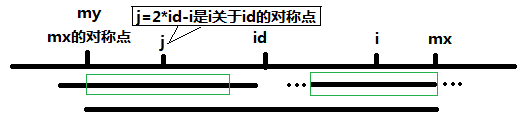
当 P[j] >= mx - i 的时候,以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中,但是基于对称性可知,下图中两个绿框所包围的部分是相同的,也就是说以S[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx - i。至于mx之后的部分是否对称,再具体匹配。
此外,对于 mx <= i 的情况,因为无法对 P[i]做更多的假设,只能让P[i] = 1,然后再去匹配。
综上,关键代码如下:
```c
//输入,并处理得到字符串s
int p[1000], mx = 0, id = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++)
{
p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
while (s[i + p[i]] == s[i - p[i]])
p[i]++;
if (i + p[i] > mx)
{
mx = i + p[i];
id = i;
}
}
//找出p[i]中最大的
```
此Manacher算法使用id、mx做配合,可以在每次循环中,直接对P[i]的快速赋值,从而在计算以i为中心的回文子串的过程中,不必每次都从1开始比较,减少了比较次数,最终使得求解最长回文子串的长度达到线性O(N)的时间复杂度。
参考:http://www.felix021.com/blog/read.php?2040 。另外,这篇文章也不错:http://leetcode.com/2011/11/longest-palindromic-substring-part-ii.html 。
- 程序员如何准备面试中的算法
- 第一部分 数据结构
- 第一章 字符串
- 1.0 本章导读
- 1.1 旋转字符串
- 1.2 字符串包含
- 1.3 字符串转换成整数
- 1.4 回文判断
- 1.5 最长回文子串
- 1.6 字符串的全排列
- 1.10 本章习题
- 第二章 数组
- 2.0 本章导读
- 2.1 寻找最小的 k 个数
- 2.2 寻找和为定值的两个数
- 2.3 寻找和为定值的多个数
- 2.4 最大连续子数组和
- 2.5 跳台阶
- 2.6 奇偶排序
- 2.7 荷兰国旗
- 2.8 矩阵相乘
- 2.9 完美洗牌
- 2.15 本章习题
- 第三章 树
- 3.0 本章导读
- 3.1 红黑树
- 3.2 B树
- 3.3 最近公共祖先LCA
- 3.10 本章习题
- 第二部分 算法心得
- 第四章 查找匹配
- 4.1 有序数组的查找
- 4.2 行列递增矩阵的查找
- 4.3 出现次数超过一半的数字
- 第五章 动态规划
- 5.0 本章导读
- 5.1 最大连续乘积子串
- 5.2 字符串编辑距离
- 5.3 格子取数
- 5.4 交替字符串
- 5.10 本章习题
- 第三部分 综合演练
- 第六章 海量数据处理
- 6.0 本章导读
- 6.1 关联式容器
- 6.2 分而治之
- 6.3 simhash算法
- 6.4 外排序
- 6.5 MapReduce
- 6.6 多层划分
- 6.7 Bitmap
- 6.8 Bloom filter
- 6.9 Trie树
- 6.10 数据库
- 6.11 倒排索引
- 6.15 本章习题
- 第七章 机器学习
- 7.1 K 近邻算法
- 7.2 支持向量机
- 附录 更多题型
- 附录A 语言基础
- 附录B 概率统计
- 附录C 智力逻辑
- 附录D 系统设计
- 附录E 操作系统
- 附录F 网络协议
- sift算法
- sift算法的编译与实现
- 教你一步一步用c语言实现sift算法、上
- 教你一步一步用c语言实现sift算法、下
- 其它
- 40亿个数中快速查找
- hash表算法
- 一致性哈希算法
- 倒排索引关键词不重复Hash编码
- 傅里叶变换算法、上
- 傅里叶变换算法、下
- 后缀树
- 基于给定的文档生成倒排索引的编码与实践
- 搜索关键词智能提示suggestion
- 最小操作数
- 最短摘要的生成
- 最长公共子序列
- 木块砌墙原稿
- 附近地点搜索
- 随机取出其中之一元素
