[TOC]
## 1. 什么是聚类
* **机器学习的分类:**
* **监督式学习**:训练集有明确答案,监督学习就是寻找问题(又称输入、特征、自变量)与答案(又称输出、目标、因变量)之间关系的学习方式。监督学习模型有两类,分类和回归。
* • 分类模型:目标变量是离散的分类型变量;
* • 回归模型:目标变量是连续性数值型变量。
* **无监督学习**:只有数据,无明确答案,即训练集没有标签。常见的无监督学习算法有聚类(clustering),由计算机自己找出规律,把有相似属性的样本放在一组,每个组也称为簇(cluster)。
* 最早的聚类分析是在考古分类、昆虫分类研究中发展起来的,目的是找到隐藏于数据中客观存在的“自然小类”,“自然小类”具有类内结构相似、类间结构差异显著的特点,**通过刻画“自然小类”可以发现数据中的规律、揭示数据的内在结构**。
* 之前一起学了**回归算法**中超级典型的线性回归,**分类算法**中非常难懂的SVM,这两都是**有监督学习**中的模型,那今天就来看看**无监督学习**中最最基础的**聚类算法**——K-Means Cluster吧。
## 2. K-Means步骤
* K-Means聚类步骤是一个循环迭代的算法,非常简单易懂:
* 1. 假定我们要对N个样本观测做聚类,要求聚为K类,首先选择K个点作为**初始中心点**;
* 2. 接下来,按照**距离初始中心点最小**的原则,把所有观测分到各中心点所在的类中;
* 3. 每类中有若干个观测,计算K个类中**所有样本点的均值**,作为第二次迭代的K个中心点;
* 4. 然后根据这个中心重复第2、3步,直到**收敛(中心点不再改变或达到指定的迭代次数)**,聚类过程结束。
* 以二维平面中的点![[公式]](https://www.zhihu.com/equation?tex=X_%7Bi%7D%3D%28x_%7Bi1%7D%2Cx_%7Bi2%7D%29%2Ci%3D1%2C...%2Cn)为例,用图片展示K=2时的迭代过程:
:-: 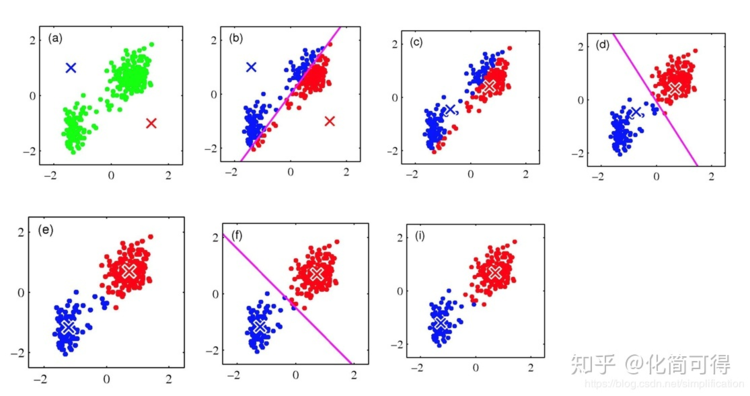
* 1. 现在我们要将(a)图中的n个绿色点聚为2类,先随机选择蓝叉和红叉分别作为初始中心点;
* 2. 分别计算所有点到初始蓝叉和初始红叉的距离,![[公式]](https://www.zhihu.com/equation?tex=X_%7Bi%7D%3D%28x_%7Bi1%7D%2Cx_%7Bi2%7D%29)距离蓝叉更近就涂为蓝色,距离红叉更近就涂为红色,遍历所有点,直到全部都染色完成,如图(b);
* 3. 现在我们不管初始蓝叉和初始红叉了,对于已染色的红色点计算其红色中心,蓝色点亦然,得到第二次迭代的中心,如图(c);
* 4. 重复第2、3步,直到收敛,聚类过程结束。
* 看完K-Means算法步骤的文字描述,我们可能会有以下疑问:
* 1. 第一步中的**初始中心点怎么确定**?随便选吗?不同的初始点得到的最终聚类结果也不同吗?
* 2. 第二步中**点之间的距离**用什么来定义?
* 3. 第三步中的**所有点的均值**(新的中心点)怎么算?
* 4. **K怎么选择**?
## 3. K-Means的数学描述
* 我们先解答第2个和第3个问题,其他两个问题放到后面小节中再说。
*
* 聚类是把相似的物体聚在一起,这个相似度(或称距离)是用什么来度量的呢?——**欧氏距离**。
*
* 给定两个样本![[公式]](https://www.zhihu.com/equation?tex=X%3D%28x_%7B1%7D%2Cx_%7B2%7D%2C...%2Cx_%7Bn%7D%29)与![[公式]](https://www.zhihu.com/equation?tex=Y%3D%28y_%7B1%7D%2Cy_%7B2%7D%2C...%2Cy_%7Bn%7D%29),其中n表示特征数 ,X和Y两个向量间的欧氏距离(Euclidean Distance)表示为:
* :-: ![[公式]](https://www.zhihu.com/equation?tex=dist_%7Bed%7D%28X%2CY%29%3D%7C%7CX-Y%7C%7C%7B2%7D%3D%5Csqrt%5B2%5D%7B%28x%7B1%7D-y_%7B1%7D%29%5E%7B2%7D%2B...%2B%28x_%7Bn%7D-y_%7Bn%7D%29%5E%7B2%7D%7D)
*
* k-means算法是把数据给分成不同的簇,目标是同一个簇中的差异小,不同簇之间的差异大,这个目标怎么用数学语言描述呢?我们一般用**误差平方和**作为目标函数(想想线性回归中说过的残差平方和、损失函数,是不是很相似),公式如下:
* :-: 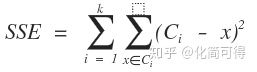
* 其中C表示聚类中心,如果x属于Ci这个簇,则计算两者的欧式距离,将所有样本点到其中心点距离算出来,并加总,就是k-means的目标函数。实现同一个簇中的样本差异小,就是最小化SSE。
*
* 我们知道,可以通过求导来求函数的极值,我们对SSE求偏导看看能得到什么结果:
*
* :-: 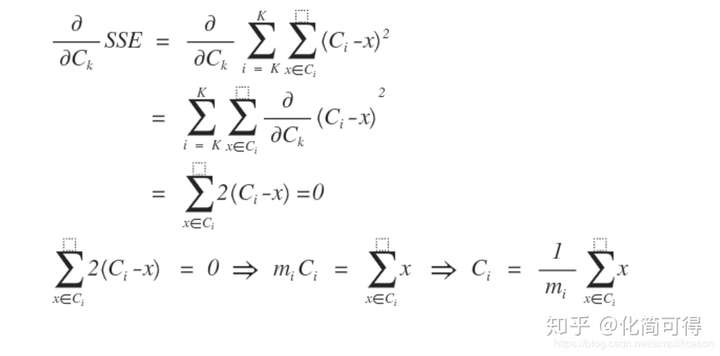
* 式中m是簇中点的数量,发现了没有,这个C的解,就是X的均值点。多点的均值点应该很好理解吧,给定一组点![[公式]](https://www.zhihu.com/equation?tex=X_%7B1%7D%2C...%2CX_%7Bm%7D),其中![[公式]](https://www.zhihu.com/equation?tex=X_%7Bi%7D%3D%28x_%7Bi1%7D%2Cx_%7Bi2%7D%2C...%2Cx_%7Bin%7D%29),这组点的均值向量表示为:
*
* ![[公式]](https://www.zhihu.com/equation?tex=++++C%3D%28%5Cfrac%7Bx_%7B11%7D%2B...%2Bx_%7B1n%7D%7D%7Bm%7D%2C...%2C%5Cfrac%7Bx_%7Bm1%7D%2B...%2Bx_%7Bmn%7D%7D%7Bm%7D%29%3D%5Cfrac%7B%5Csum+x%7D%7Bm%7D)
## 4. 初始中心点怎么确定
* 在k-means算法步骤中,有两个地方降低了SSE:
*
* 1. 把样本点分到最近邻的簇中,这样会降低SSE的值;
* 2. 重新优化聚类中心点,进一步的减小了SSE。
*
* 这样的重复迭代、不断优化,会找到**局部最优解(局部最小的SSE)**,如果想要找到全局最优解需要找到合理的初始聚类中心。
*
* 那合理的初始中心怎么选?
*
* 方法有很多,譬如先随便选个点作为第1个初始中心C1,接下来计算所有样本点与C1的距离,距离最大的被选为下一个中心C2,直到选完K个中心。这个算法叫做**K-Means++**,可以理解为 K-Means的改进版,它可以能有效地解决初始中心的选取问题,但**无法解决离群点问题**。
*
* 我自己也想了一个方法,先找所有样本点的均值点,计算每个点与均值点的距离,选取最远的K个点作为K个初始中心。当然,如果样本中有离群点,这个方法也不佳。
*
* 总的来说,最好解决办法还是多尝试几次,即**多设置几个不同的初始点**,从中选最优,也就是具有最小SSE值的那组作为最终聚类。
## 5. K值怎么确定
* 要知道,**K设置得越大,样本划分得就越细,每个簇的聚合程度就越高,误差平方和SSE自然就越小**。所以不能单纯像选择初始点那样,用不同的K来做尝试,选择SSE最小的聚类结果对应的K值,因为这样选出来的肯定是你尝试的那些K值中最大的那个。
*
* 确定K值的一个主流方法叫“**手肘法**”。
*
* 如果我们拿到的样本,客观存在J个“自然小类”,这些真实存在的小类是隐藏于数据中的。三维以下的数据我们还能画图肉眼分辨一下J的大概数目,更高维的就不能直观地看到了,我们只能从一个比较小的K,譬如K=2开始尝试,去逼近这个真实值J。
*
* * 当K小于样本真实簇数J时,K每增大一个单位,就会大幅增加每个簇的聚合程度,这时SSE的下降幅度会很大;
* * 当K接近J时,再增加K所得到的聚合程度回报会迅速变小,SSE的下降幅度也会减小;
* * 随着K的继续增大,SSE的变化会趋于平缓。
*
* 例如下图,真实的J我们事先不知道,那么从K=2开始尝试,发现K=3时,SSE大幅下降,K=4时,SSE下降幅度稍微小了点,K=5时,下降幅度急速缩水,再后面就越来越平缓。所以我们认为J应该为4,因此可以将K设定为4。
* :-: 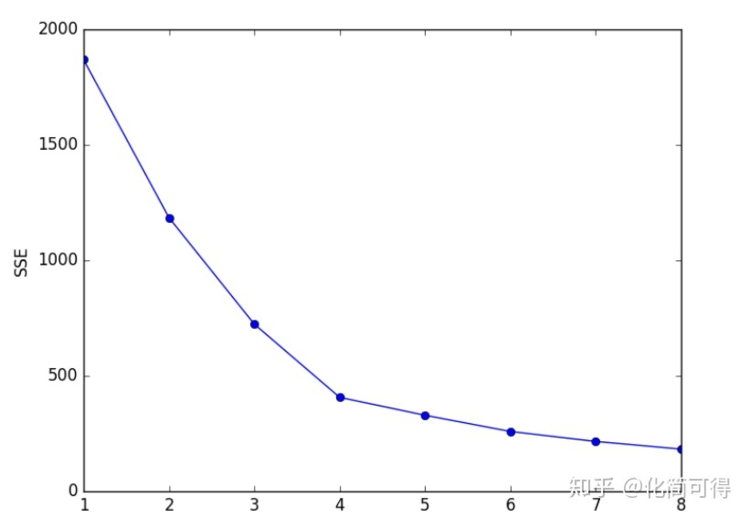
* 叫“手肘法”可以说很形象了,因为SSE和K的关系图就像是手肘的形状,而**肘部对应的K值就被认为是数据的真实聚类数**。
*
* 当然还有其他设定K值的方法,这里不赘述,总的来说还是要结合自身经验多做尝试,要知道没有一个方法是完美的。
*
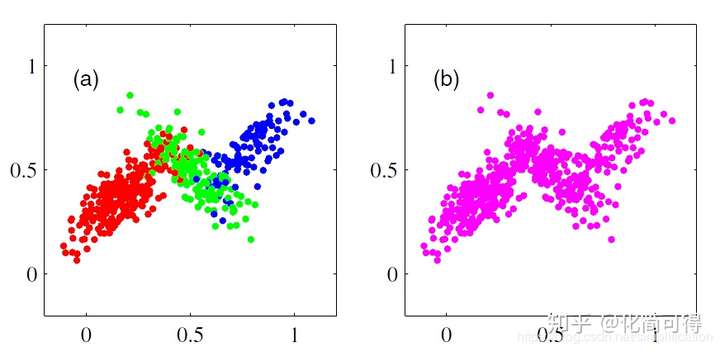
* 而且,聚类有时是比较主观的事,比如下面这组点,真实簇数J是几呢?我们既可以说J=3,也可以就把它分成2个簇。
*
* 
## 6. 小结
* K-Means优点在于原理简单,容易实现,聚类效果好。
*
* 当然,也有一些缺点:
*
* 1. K值、初始点的选取不好确定;
* 2. 得到的结果只是局部最优;
* 3. 受离群值影响大。
