[TOC]
## 数据清洗
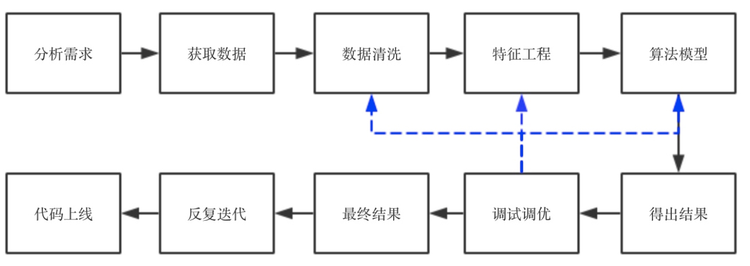
* 来了项目,首先是分析项目的目的和需求,了解这个项目属于什么问题,要达到什么效果。然后提取数据,做基本的数据清洗。第三步是特征工程,这个属于脏活累活,需要耗费很大的精力,如果特征工程做的好,那么,后面选择什么算法其实差异不大,反之,不管选择什么算法,效果都不会有突破性的提高。第四步,是跑算法,通常情况下,我会把所有能跑的算法先跑一遍,看看效果,分析一下precesion/recall和f1-score,看看有没有什么异常(譬如有好几个算法precision特别好,但是recall特别低,这就要从数据中找原因,或者从算法中看是不是因为算法不适合这个数据),如果没有异常,那么就进行下一步,选择一两个跑的结果最好的算法进行调优。调优的方法很多,调整参数的话可以用网格搜索、随机搜索等,调整性能的话,可以根据具体的数据和场景进行具体分析。调优后再跑一边算法,看结果有没有提高,如果没有,找原因,数据 or 算法?是数据质量不好,还是特征问题还是算法问题。一个一个排查,找解决方法。特征问题就回到第三步再进行特征工程,数据质量问题就回到第一步看数据清洗有没有遗漏,异常值是否影响了算法的结果,算法问题就回到第四步,看算法流程中哪一步出了问题。如果实在不行,可以搜一下相关的论文,看看论文中有没有解决方法。这样反复来几遍,就可以出结果了,写技术文档和分析报告,再向业务人员或产品讲解我们做的东西,然后他们再提建议/该需求,不断循环,最后代码上线,改bug,直到结项。
* 直观来看,可以用一个流程图来表示:
* 
* 为什么要进行数据清洗呢?我们在书上看到的数据,譬如常见的iris数据集,房价数据,电影评分数据集等等,数据质量都很高,没有缺失值,没有异常点,也没有噪音,而在真实数据中,我们拿到的数据可能包含了大量的缺失值,可能包含大量的噪音,也可能因为人工录入错误导致有异常点存在,对我们挖据出有效信息造成了一定的困扰,所以我们需要通过一些方法,尽量提高数据的质量。数据清洗一般包括以下几个步骤:
* 一、分析数据
* 二、缺失值处理
* 三、异常值处理
* 四、去重处理
* 五、噪音数据处理
* 六、一些实用的数据处理小工具
### 一、分析数据
* 在实际项目中,当我们确定需求后就会去找相应的数据,拿到数据后,首先要对数据进行描述性统计分析,查看哪些数据是不合理的,也可以知道数据的基本情况。如果是销售额数据可以通过分析不同商品的销售总额、人均消费额、人均消费次数等,同一商品的不同时间的消费额、消费频次等等,了解数据的基本情况。此外可以通过作图的方式了解数据的质量,有无异常点,有无噪音等。举个例子(这里数据较少,就直接用R作图了):
```
#一组年薪超过10万元的经理收入
pay=c(11,19,14,22,14,28,13,81,12,43,11,16,31,16,23.42,22,26,17,22,13,27,180,16,43,82,14,11,51,76,28,66,29,14,14,65,37,16,37,35,39,27,14,17,13,38,28,40,85,32,25,26,16,12,54,40,18,27,16,14,33,29,77,50,19,34)
par(mfrow=c(2,2))#将绘图窗口改成2*2,可同时显示四幅图
hist(pay)#绘制直方图
dotchart(pay)#绘制点图
barplot(pay,horizontal=T)#绘制箱型图
qqnorm(pay);qqline(pay)#绘制Q-Q图
```
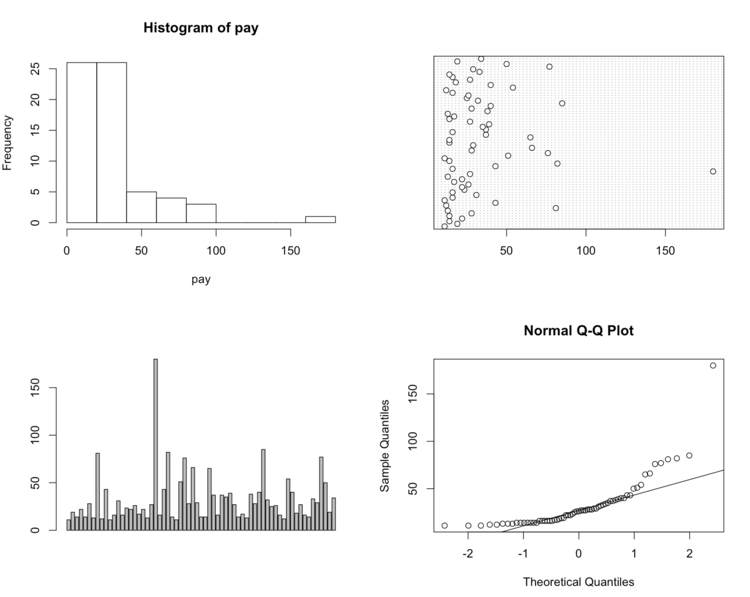
* 从上面四幅图可以很清楚的看出,180是异常值,即第23个数据需要清理。
* python中也包含了大量的统计命令,其中主要的统计特征函数如下图所示:

### 二、缺失值处理
* 缺失值在实际数据中是不可避免的问题,有的人看到有缺失的数据就直接删除了,有的人直接赋予0值或者某一个特殊的值,那么到底该怎么处理呢?对于不同的数据场景应该采取不同的策略,首先应该判断缺失值的分布情况:
```
1 import scipy as sp
2 data = sp.genfromtxt("web_traffic.tsv",delimiter = "\t")
```
* 数据情况如下:
```
>>>data
array([[ 1.00000000e+00, 2.27200000e+03],
[ 2.00000000e+00, nan],
[ 3.00000000e+00, 1.38600000e+03],
...,
[ 7.41000000e+02, 5.39200000e+03],
[ 7.42000000e+02, 5.90600000e+03],
[ 7.43000000e+02, 4.88100000e+03]])
>>> print data[:10]
[[ 1.00000000e+00 2.27200000e+03]
[ 2.00000000e+00 nan]
[ 3.00000000e+00 1.38600000e+03]
[ 4.00000000e+00 1.36500000e+03]
[ 5.00000000e+00 1.48800000e+03]
[ 6.00000000e+00 1.33700000e+03]
[ 7.00000000e+00 1.88300000e+03]
[ 8.00000000e+00 2.28300000e+03]
[ 9.00000000e+00 1.33500000e+03]
[ 1.00000000e+01 1.02500000e+03]]
>>> data.shape
(743, 2)
```
* 可以看到,第2列已经出现了缺失值,现在我们来看一下缺失值的数量:
```
1 >>> x = data[:,0]
2 >>> y = data[:,1]
3 >>> sp.sum(sp.isnan(y))
4 8
```
* 在743个数据里只有8个数据缺失,所以删除它们对于整体数据情况影响不大。当然,这是缺失值少的情况下,在缺失值值比较多,而这个维度的信息还很重要的时候(因为缺失值如果占了95%以上,可以直接去掉这个维度的数据了),直接删除会对后面的算法跑的结果造成不好的影响。我们常用的方法有以下几种:
> 1. 直接删除----适合缺失值数量较小,并且是随机出现的,删除它们对整体数据影响不大的情况
> 2. 使用一个全局常量填充---譬如将缺失值用“Unknown”等填充,但是效果不一定好,因为算法可能会把它识别为一个新的类别,一般很少用
> 3. 使用均值或中位数代替----优点:不会减少样本信息,处理简单。缺点:当缺失数据不是随机数据时会产生偏差.对于正常分布的数据可以使用均值代替,如果数据是倾斜的,使用中位数可能更好。
>
> 4. 插补法
> 1)随机插补法----从总体中随机抽取某个样本代替缺失样本
> 2)多重插补法----通过变量之间的关系对缺失数据进行预测,利用蒙特卡洛方法生成多个完整的数据集,在对这些数据集进行分析,最后对分析结果进行汇总处理
> 3)热平台插补----指在非缺失数据集中找到一个与缺失值所在样本相似的样本(匹配样本),利用其中的观测值对缺失值进行插补。
> 优点:简单易行,准去率较高
> 缺点:变量数量较多时,通常很难找到与需要插补样本完全相同的样本。但我们可以按照某些变量将数据分层,在层中对缺失值实用均值插补
> 4)拉格朗日差值法和牛顿插值法(简单高效,数值分析里的内容,数学公式以后再补 = =)
> 5. 建模法
> 可以用回归、使用贝叶斯形式化方法的基于推理的工具或决策树归纳确定。例如,利用数据集中其他数据的属性,可以构造一棵判定树,来预测缺失值的值。
* 以上方法各有优缺点,具体情况要根据实际数据分分布情况、倾斜程度、缺失值所占比例等等来选择方法。一般而言,建模法是比较常用的方法,它根据已有的值来预测缺失值,准确率更高。
### 三、异常值处理
* 异常值我们通常也称为“离群点”。在讲分析数据时,我们举了个例子说明如何发现离群点,除了画图(画图其实并不常用,因为数据量多时不好画图,而且慢),还有很多其他方法:
1. 简单的统计分析
拿到数据后可以对数据进行一个简单的描述性统计分析,譬如最大最小值可以用来判断这个变量的取值是否超过了合理的范围,如客户的年龄为-20岁或200岁,显然是不合常理的,为异常值。
在python中可以直接用pandas的describe( ):
```
>>> import pandas as pd
>>> data = pd.read_table("web_traffic.tsv",header = None)
>>> data.describe()
0 1
count 743.000000 735.000000
mean 372.000000 1962.165986
std 214.629914 860.720997
min 1.000000 472.000000
25% 186.500000 1391.000000
50% 372.000000 1764.000000
75% 557.500000 2217.500000
max 743.000000 5906.000000
```
2. 3∂原则
如果数据服从正态分布,在3∂原则下,异常值为一组测定值中与平均值的偏差超过3倍标准差的值。如果数据服从正态分布,距离平均值3∂之外的值出现的概率为P(|x-u| > 3∂) <= 0.003,属于极个别的小概率事件。如果数据不服从正态分布,也可以用远离平均值的多少倍标准差来描述。
3. 箱型图分析
箱型图提供了识别异常值的一个标准:如果一个值小于QL01.5IQR或大于OU-1.5IQR的值,则被称为异常值。QL为下四分位数,表示全部观察值中有四分之一的数据取值比它小;QU为上四分位数,表示全部观察值中有四分之一的数据取值比它大;IQR为四分位数间距,是上四分位数QU与下四分位数QL的差值,包含了全部观察值的一半。箱型图判断异常值的方法以四分位数和四分位距为基础,四分位数具有鲁棒性:25%的数据可以变得任意远并且不会干扰四分位数,所以异常值不能对这个标准施加影响。因此箱型图识别异常值比较客观,在识别异常值时有一定的优越性。
4. 基于模型检测
首先建立一个数据模型,异常是那些同模型不能完美拟合的对象;如果模型是簇的集合,则异常是不显著属于任何簇的对象;在使用回归模型时,异常是相对远离预测值的对象
* 优缺点:1.有坚实的统计学理论基础,当存在充分的数据和所用的检验类型的知识时,这些检验可能非常有效;2.对于多元数据,可用的选择少一些,并且对于高维数据,这些检测可能性很差。
5. 基于距离
通常可以在对象之间定义邻近性度量,异常对象是那些远离其他对象的对象
* 优缺点:1.简单;2.缺点:基于邻近度的方法需要O(m2)时间,大数据集不适用;3.该方法对参数的选择也是敏感的;4.不能处理具有不同密度区域的数据集,因为它使用全局阈值,不能考虑这种密度的变化。
6. 基于密度
当一个点的局部密度显著低于它的大部分近邻时才将其分类为离群点。适合非均匀分布的数据。
* 优缺点:1.给出了对象是离群点的定量度量,并且即使数据具有不同的区域也能够很好的处理;2.与基于距离的方法一样,这些方法必然具有O(m2)的时间复杂度。对于低维数据使用特定的数据结构可以达到O(mlogm);3.参数选择困难。虽然算法通过观察不同的k值,取得最大离群点得分来处理该问题,但是,仍然需要选择这些值的上下界。
7. 基于聚类:
基于聚类的离群点:一个对象是基于聚类的离群点,如果该对象不强属于任何簇。离群点对初始聚类的影响:如果通过聚类检测离群点,则由于离群点影响聚类,存在一个问题:结构是否有效。为了处理该问题,可以使用如下方法:对象聚类,删除离群点,对象再次聚类(这个不能保证产生最优结果)。
* 优缺点:1.基于线性和接近线性复杂度(k均值)的聚类技术来发现离群点可能是高度有效的;2.簇的定义通常是离群点的补,因此可能同时发现簇和离群点;3.产生的离群点集和它们的得分可能非常依赖所用的簇的个数和数据中离群点的存在性;4.聚类算法产生的簇的质量对该算法产生的离群点的质量影响非常大。
**处理方法:**
1. 删除异常值----明显看出是异常且数量较少可以直接删除
2. 不处理---如果算法对异常值不敏感则可以不处理,但如果算法对异常值敏感,则最好不要用,如基于距离计算的一些算法,包括kmeans,knn之类的。
3. 平均值替代----损失信息小,简单高效。
4. 视为缺失值----可以按照处理缺失值的方法来处理
### 四、去重处理
以DataFrame数据格式为例:
```
#创建数据,data里包含重复数据
>>> data = pd.DataFrame({'v1':['a']*5+['b']* 4,'v2':[1,2,2,2,3,4,4,5,3]})
>>> data
v1 v2
0 a 1
1 a 2
2 a 2
3 a 2
4 a 3
5 b 4
6 b 4
7 b 5
8 b 3
#DataFrame的duplicated方法返回一个布尔型Series,表示各行是否是重复行
>>> data.duplicated()
0 False
1 False
2 True
3 True
4 False
5 False
6 True
7 False
8 False
dtype: bool
#drop_duplicates方法用于返回一个移除了重复行的DataFrame
>>> data.drop_duplicates()
v1 v2
0 a 1
1 a 2
4 a 3
5 b 4
7 b 5
8 b 3
#这两个方法默认会判断全部列,你也可以指定部分列进行重复项判断。假设你还有一列值,且只希望根据v1列过滤重复项:
>>> data['v3']=range(9)
>>> data
v1 v2 v3
0 a 1 0
1 a 2 1
2 a 2 2
3 a 2 3
4 a 3 4
5 b 4 5
6 b 4 6
7 b 5 7
8 b 3 8
>>> data.drop_duplicates(['v1'])
v1 v2 v3
0 a 1 0
5 b 4 5
#duplicated和drop_duplicates默认保留的是第一个出现的值组合。传入take_last=True则保留最后一个:
>>> data.drop_duplicates(['v1','v2'],take_last = True)
v1 v2 v3
0 a 1 0
3 a 2 3
4 a 3 4
6 b 4 6
7 b 5 7
8 b 3 8
```
* 如果数据是列表格式的,有以下几种方法可以删除:
```
list0=['b','c', 'd','b','c','a','a']
方法1:使用set()
list1=sorted(set(list0),key=list0.index) # sorted output
print( list1)
方法2:使用 {}.fromkeys().keys()
list2={}.fromkeys(list0).keys()
print(list2)
方法3:set()+sort()
list3=list(set(list0))
list3.sort(key=list0.index)
print(list3)
方法4:迭代
list4=[]
for i in list0:
if not i in list4:
list4.append(i)
print(list4)
方法5:排序后比较相邻2个元素的数据,重复的删除
def sortlist(list0):
list0.sort()
last=list0[-1]
for i in range(len(list0)-2,-1,-1):
if list0[i]==last:
list0.remove(list0[i])
else:
last=list0[i]
return list0
print(sortlist(list0))
```
### 五、噪音处理
* 噪音,是被测量变量的随机误差或方差。我们在上文中提到过异常点(离群点),那么离群点和噪音是不是一回事呢?我们知道,观测量(Measurement) = 真实数据(True Data) + 噪声 (Noise)。离群点(Outlier)属于观测量,既有可能是真实数据产生的,也有可能是噪声带来的,但是总的来说是和大部分观测量之间有明显不同的观测值。。噪音包括错误值或偏离期望的孤立点值,但也不能说噪声点包含离群点,虽然大部分数据挖掘方法都将离群点视为噪声或异常而丢弃。然而,在一些应用(例如:欺诈检测),会针对离群点做离群点分析或异常挖掘。而且有些点在局部是属于离群点,但从全局看是正常的。
* 在quora上看到过一个解释噪音与离群点的有趣的例子:
> 离群点: 你正在从口袋的零钱包里面穷举里面的钱,你发现了3个一角,1个五毛,和一张100元的毛爷爷向你微笑。这个100元就是个离群点,因为并不应该常出现在口袋里..
噪声: 你晚上去三里屯喝的酩酊大醉,很需要买点东西清醒清醒,这时候你开始翻口袋的零钱包,嘛,你发现了3个一角,1个五毛,和一张100元的毛爷爷向你微笑。但是你突然眼晕,把那三个一角看成了三个1元...这样错误的判断使得数据集中出现了噪声
* 那么对于噪音我们应该如何处理呢?有以下几种方法:
*
**1. 分箱法**
分箱方法通过考察数据的“近邻”(即,周围的值)来光滑有序数据值。这些有序的值被分布到一些“桶”或箱中。由于分箱方法考察近邻的值,因此它进行局部光滑。
* 用箱均值光滑:箱中每一个值被箱中的平均值替换。
* 用箱中位数平滑:箱中的每一个值被箱中的中位数替换。
* 用箱边界平滑:箱中的最大和最小值同样被视为边界。箱中的每一个值被最近的边界值替换。
一般而言,宽度越大,光滑效果越明显。箱也可以是等宽的,其中每个箱值的区间范围是个常量。分箱也可以作为一种离散化技术使用.
**2. 回归法**
* 可以用一个函数拟合数据来光滑数据。线性回归涉及找出拟合两个属性(或变量)的“最佳”直线,使得一个属性能够预测另一个。多线性回归是线性回归的扩展,它涉及多于两个属性,并且数据拟合到一个多维面。使用回归,找出适合数据的数学方程式,能够帮助消除噪声。
### 六、一些实用的数据处理小工具
1. **去掉文件中多余的空行**
空行主要指的是(\\n,\\r,\\r\\n,\\n\\r等),在python中有个strip()的方法,该方法可以去掉字符串两端多余的“空白”,此处的空白主要包括空格,制表符(\\t),换行符。不过亲测以后发现,strip()可以匹配掉\\n,\\r\\n,\\n\\r等,但是过滤不掉单独的\\r。为了万无一失,我还是喜欢用麻烦的办法,如下:
```
#-*- coding :utf-8 -*-
#文本格式化处理,过滤掉空行
file = open('123.txt')
i = 0
while 1:
line = file.readline().strip()
if not line:
break
i = i + 1
line1 = line.replace('\r','')
f1 = open('filename.txt','a')
f1.write(line1 + '\n')
f1.close()
print str(i)
```
2. **如何判断文件的编码格式**
```
#-*- coding:utf8 -*-
#批量处理编码格式转换(优化)
import os
import chardet
path1 = 'E://2016txtutf/'
def dirlist(path):
filelist = os.listdir(path)
for filename in filelist:
filepath = os.path.join(path, filename)
if os.path.isdir(filepath):
dirlist(filepath)
else:
if filepath.endswith('.txt'):
f = open(filepath)
data = f.read()
if chardet.detect(data)['encoding'] != 'utf-8':
print filepath + "----"+ chardet.detect(data)['encoding']
dirlist(path1)
```
3. **文件编码格式转换,gbk与utf-8之间的转换**
这个主要是在一些对文件编码格式有特殊需求的时候,需要批量将gbk的转utf-8的或者将utf-8编码的文件转成gbk编码格式的。
```
#-*- coding:gbk -*-
#批量处理编码格式转换
import codecs
import os
path1 = 'E://dir/'
def ReadFile(filePath,encoding="utf-8"):
with codecs.open(filePath,"r",encoding) as f:
return f.read()
def WriteFile(filePath,u,encoding="gbk"):
with codecs.open(filePath,"w",encoding) as f:
f.write(u)
def UTF8_2_GBK(src,dst):
content = ReadFile(src,encoding="utf-8")
WriteFile(dst,content,encoding="gbk")
def GBK_2_UTF8(src,dst):
content = ReadFile(src,encoding="gbk")
WriteFile(dst,content,encoding="utf-8")
def dirlist(path):
filelist = os.listdir(path)
for filename in filelist:
filepath = os.path.join(path, filename)
if os.path.isdir(filepath):
dirlist(filepath)
else:
if filepath.endswith('.txt'):
print filepath
#os.rename(filepath, filepath.replace('.txt','.doc'))
try:
UTF8_2_GBK(filepath,filepath)
except Exception,ex:
f = open('error.txt','a')
f.write(filepath + '\n')
f.close()
dirlist(path1)
```
