[TOC] >[success] # 复杂度分析系方式 ~~~ 1.只关注循环执行次数最多的一段代码 2.加法法则：总复杂度等于量级最大的那段代码的复杂度 -- max 原则 3.乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积 4.O(m+n)、O(m*n)法则 原则：'通常会忽略掉公式中的常量、低阶、系数' ~~~ >[danger] ##### 只关注循环执行次数最多的一段代码 ~~~ 1.大 O 复杂度表示无穷大渐近，因此是一种变化趋势的表现，通常会忽略掉 公式中的常量、低阶、系数，只需要记录一个最大阶的量级就可以了，因此 分析一个算法、一段代码的时间复杂度的时候，也只关注'循环执行次数最多'的 那一段代码就可以了 2.下面的案例中利用这个理论得出的公式是：T(n) = O(n) ~~~ ~~~ function cal(n) { let sum = 0 // 运行时间 1 个unit_time let i = 1 // 运行时间 1 个unit_time for(;i<=n;i++){ // 运行时间 n 个unit_time sum = sum + i // 运行时间 n 个unit_time } return sum } console.log(cal(10)) // 55 ~~~ >[danger] ##### 加法法则：总复杂度等于量级最大的那段代码的复杂度 -- max 原则 ~~~ 1.通常遵循原则'忽略掉公式中的常量、低阶、系数' 因此下面代码第一段循环 '100'是个常量执行时间，跟n（'数据的规模的大小'）的规模无关因此可以忽略 '对第一条的解释(极客时间中王争老师对着段的解释如下):' 即便这段代码循环 10000 次、100000 次，只要是一个已知的数，跟 n 无关， 照样也是常量级的执行时间。当 n 无限大的时候，就可以忽略。 尽管对代码的执行时间会有很大影响，但是回到时间复杂度的概念来说， 它表示的是一个算法执行效率与数据规模增长的变化趋势，所以不管常量的执行时间多大， 我们都可以忽略掉。因为它本身对增长趋势并没有影响。 '我的简单理解：' 因为是常量是固定在哪里的，但是'n'（'数据的规模的大小'）是非固定的可能是十亿百亿， 如果是这些那想对比100，这个100完全可以忽略也遵循了'大 O 复杂度表示无穷大渐近' 2.当一段代码中有多段代码他们都和'n'（'数据的规模的大小'），这时候需要遵循的是： '总的时间复杂度等于量级最大的那段代码的时间复杂度',用公式表示的话： 如果' T1(n)=O(f(n))；T2(n)=O(g(n))'那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n))) ,即也就是说取两个中最大的作为代码的时间复杂度表示 3.分析下面案例： T1(n) = O(n);T2(n) = O(n^2) 因此 T(n) = T1(n)+T2(n) = max(O(n),O(n^2) ) 最后得出：T(n) = O(n^2) ~~~ ~~~ function cal(n){ let sum1 = 0 let p = 1 // ---- 这段代码开始 ---- // 100 是常量 和 可能是无穷的N相比可以忽略 // 因此不考虑在我们的时间复杂度中 for(;p<100;p++){ sum1+=p } // --- 这段代码结束 --- let sum2 = 0 let q = 1 // ---- 这段代码开始 ---- // 和 n 有关因此考虑在复杂度中 // 表达公式T(n) = O(n) for(;q<n;q++){ sum1+=q } // --- 这段代码结束 --- let sum3 = 0 let i = 1 let j = 1 // ---- 这段代码开始 ---- // 和 n 有关因此考虑在复杂度中 // 表达公式T(n) = O(n^2) for(;i<=n;i++){ for(;j<=n;j++){ sum3+=i*j } } // --- 这段代码结束 --- return sum3+sum1+sum2 } ~~~ >[danger] ##### 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积 ~~~ 1.下面代码和上面的代码n^2 哪里类似，这里就不用js的表现形式，直接使用了 '极客时间王争老师的代码' 2.下面的代码看到后，先按照第一个法则'关注循环执行次数最多的一段代码', 最多的就是'循环嵌套'，在按照第二个法则'总复杂度等于量级最大的那段代码的复杂度 -- max 原则' 整段'cal'只有一段代码，因此直接可以忽略，现在按照第三条'嵌套代码的复杂度等于嵌套内外代码复杂度的乘积' 外层代码'n' 内层代码也为'n',因此最后得出：T(n) = O(n^2) ~~~ ~~~ int cal(int n) { int ret = 0; int i = 1; for (; i < n; ++i) { ret = ret + f(i); // 循环嵌套 } } int f(int n) { int sum = 0; int i = 1; for (; i < n; ++i) { sum = sum + i; } return sum; } ~~~ >[danger] ##### O(m+n)、O(m*n)法则 ~~~ 1.我们刚才的加法法则是在两段代码都是受控制与一个变量，我们遵循max取最大，但是 两段代码的控制变量分别是用两个'数据的规模的大小'的变量控制，例如下面的代码中的m 和n 分别控制各自的数据规模这时候就不能用'max'方法去取，而是两者求和，乘法不变还是 相乘 2.因此下面的公式为：T(m)+T(n) = O(f(m)+f(n)) ~~~ ~~~ int cal(int m, int n) { int sum_1 = 0; int i = 1; for (; i < m; ++i) { sum_1 = sum_1 + i; //T(m) = O(m) } int sum_2 = 0; int j = 1; for (; j < n; ++j) { sum_2 = sum_2 + j; // T(n) = O(n) } return sum_1 + sum_2; } ~~~ >[info] ## 常见时间复杂度 ~~~ 1.O(1): Constant Complexity: Constant 常数复杂度 2.O(log n): Logarithmic Complexity: 对数复杂度 3.O(n): Linear Complexity: 线性时间复杂度 4.O(n^2): N square Complexity平方 5.O(n^3): N square Complexity ⽴立⽅ 6.O(2^n): Exponential Growth 指数 7.O(n!): Factorial 阶乘 ~~~ [图片来源极客时间](https://time.geekbang.org/column/article/40036)  >[danger] ##### 时间复杂度划分 --- 多项式量级、非多项式（NP）量级 ~~~ 1.多项式量级——随着数据规模的增长，算法的执行时间和空间占用统一呈 多项式规律增长 2.非多项式量级——随着数据量n的增长，时间复杂度急剧增长，执行时间无 限增加 3.解释：把时间复杂度为非多项式量级的算法问题叫做NP（Non- Deterministic Polynomial,非确定多项式）问题，当数据规模n越大时，非多 项式量级算法的执行时间会急剧增加，求解问题的执行时间会无线增长。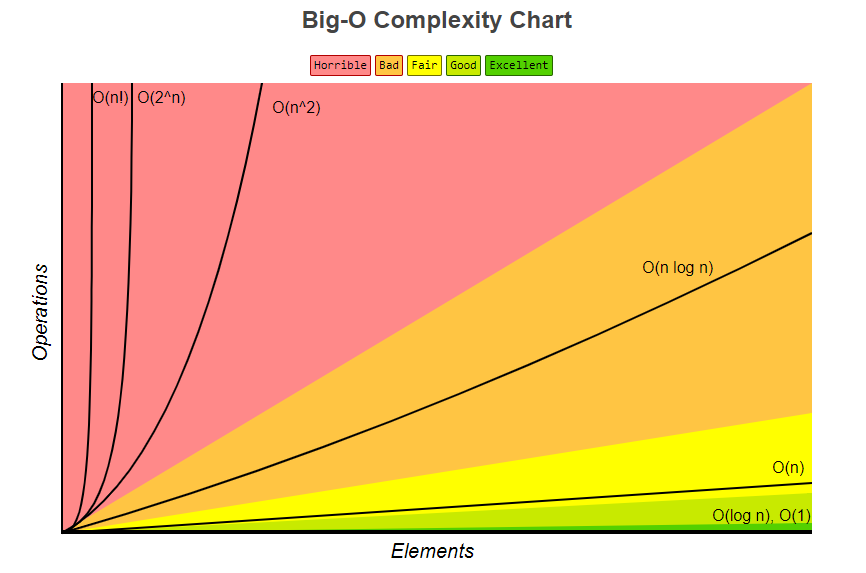所 以，'非多项式时间复杂度的算法其实是非常低效的算法' 4.通过下图和下表也可看出来'非多项式量级'即使n的数据的规模的很小，他 的运算效率也是急速骤增的，因此'非多项式时间复杂度的算法其实是非常低效的算法' ~~~ * 附一张大O复杂度的图[参考网站](https://www.bigocheatsheet.com/)  >[danger] ##### 将上面常见的进行归类 | 多项式量级 | 非多项式量级 | | --- | --- | | O(1) 常量阶 | O(2^n)指数 | | O(log n) 对数阶 | O(n!): Factorial 阶乘 | | O(n) 线性阶 | | | O(nlog n) 线性对数阶 | | | O(n^2)/O(n^3) 平方阶/立方阶 | | >[danger] ##### O(1) ~~~ 1.O(1) 只是常量级时间复杂度的一种表示方法，并不是指只执行了一行代码。 2.简单的说：只要代码的执行时间不随 n 的增大而增长，这样代码的时间复杂度我们都记作 O(1)。只要算法中不存在'循环语句'、'递归语句'，即使有成千上万行的代码，其时间复杂度也是Ο(1) 3.下面的代码，即便有 3 行，它的时间复杂度也是 O(1），而不是 O(3)。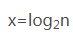 ~~~ ~~~ let name = 'wang' let age= '18' ~~~ >[danger] ##### O(logn)、O(nlogn) ~~~ 1.分析下面代码执行，如果'n'(数据规模的大小)，为1则下面的代码会走1次，n为2则会走2次， n为'3-6'走3次，如果取出他们最大节点可以表示为 ：2^0 = 1 / 2^1 =2 / 2^3 = 6 ，其中等号右边 是下面代码中变量'n'表示数据规模大小，左边的次幂是代码在这运行了几次（也就是多少时间）， 假如代码运行了'x' 次，那他所对应的数据规模'n'我们还是用n表示 即下面的代码则为：2^x = n, 想求x的次数（这里x次数其实表示的是代码运行时间），相求x（也就是运行时间），得到公式如下图: 2.因此他时间复杂度则为T(n) = O(log2^n) ~~~  ~~~ i=1; while (i <= n) { i = i * 2; } ~~~ * 同理下面的代码T(n) = O(log3^n) ~~~ i=1; while (i <= n) { i = i * 3; } ~~~