# L2 正则化：岭回归 > 原文：[https://www.bookbookmark.ds100.org/ch/16/reg_ridge.html](https://www.bookbookmark.ds100.org/ch/16/reg_ridge.html) ``` # HIDDEN # Clear previously defined variables %reset -f # Set directory for data loading to work properly import os os.chdir(os.path.expanduser('~/notebooks/16')) ``` ``` # HIDDEN import warnings # Ignore numpy dtype warnings. These warnings are caused by an interaction # between numpy and Cython and can be safely ignored. # Reference: https://stackoverflow.com/a/40846742 warnings.filterwarnings("ignore", message="numpy.dtype size changed") warnings.filterwarnings("ignore", message="numpy.ufunc size changed") import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns %matplotlib inline import ipywidgets as widgets from ipywidgets import interact, interactive, fixed, interact_manual import nbinteract as nbi sns.set() sns.set_context('talk') np.set_printoptions(threshold=20, precision=2, suppress=True) pd.options.display.max_rows = 7 pd.options.display.max_columns = 8 pd.set_option('precision', 2) # This option stops scientific notation for pandas # pd.set_option('display.float_format', '{:.2f}'.format) ``` ``` # HIDDEN def df_interact(df, nrows=7, ncols=7): ''' Outputs sliders that show rows and columns of df ''' def peek(row=0, col=0): return df.iloc[row:row + nrows, col:col + ncols] if len(df.columns) <= ncols: interact(peek, row=(0, len(df) - nrows, nrows), col=fixed(0)) else: interact(peek, row=(0, len(df) - nrows, nrows), col=(0, len(df.columns) - ncols)) print('({} rows, {} columns) total'.format(df.shape[0], df.shape[1])) ``` ``` # HIDDEN df = pd.read_csv('water_large.csv') ``` ``` # HIDDEN from collections import namedtuple Curve = namedtuple('Curve', ['xs', 'ys']) def flatten(seq): return [item for subseq in seq for item in subseq] def make_curve(clf, x_start=-50, x_end=50): xs = np.linspace(x_start, x_end, num=100) ys = clf.predict(xs.reshape(-1, 1)) return Curve(xs, ys) def plot_data(df=df, ax=plt, **kwargs): ax.scatter(df.iloc[:, 0], df.iloc[:, 1], s=50, **kwargs) def plot_curve(curve, ax=plt, **kwargs): ax.plot(curve.xs, curve.ys, **kwargs) def plot_curves(curves, cols=2, labels=None): if labels is None: labels = [f'Deg {deg} poly' for deg in degrees] rows = int(np.ceil(len(curves) / cols)) fig, axes = plt.subplots(rows, cols, figsize=(10, 8), sharex=True, sharey=True) for ax, curve, label in zip(flatten(axes), curves, labels): plot_data(ax=ax, label='Training data') plot_curve(curve, ax=ax, label=label) ax.set_ylim(-5e10, 170e10) ax.legend() # add a big axes, hide frame fig.add_subplot(111, frameon=False) # hide tick and tick label of the big axes plt.tick_params(labelcolor='none', top='off', bottom='off', left='off', right='off') plt.grid(False) plt.title('Polynomial Regression') plt.xlabel('Water Level Change (m)') plt.ylabel('Water Flow (Liters)') plt.tight_layout() ``` ``` # HIDDEN def coefs(clf): reg = clf.named_steps['reg'] return np.append(reg.intercept_, reg.coef_) def coef_table(clf): vals = coefs(clf) return (pd.DataFrame({'Coefficient Value': vals}) .rename_axis('degree')) ``` ``` # HIDDEN X = df.iloc[:, [0]].as_matrix() y = df.iloc[:, 1].as_matrix() degrees = [1, 2, 8, 12] clfs = [Pipeline([('poly', PolynomialFeatures(degree=deg, include_bias=False)), ('reg', LinearRegression())]) .fit(X, y) for deg in degrees] curves = [make_curve(clf) for clf in clfs] alphas = [0.01, 0.1, 1.0, 10.0] ridge_clfs = [Pipeline([('poly', PolynomialFeatures(degree=deg, include_bias=False)), ('reg', RidgeCV(alphas=alphas, normalize=True))]) .fit(X, y) for deg in degrees] ridge_curves = [make_curve(clf) for clf in ridge_clfs] ``` 在本节中，我们将介绍$L_2$正则化，这是一种在成本函数中惩罚大权重以降低模型方差的方法。我们简要回顾了线性回归，然后引入正则化作为对成本函数的修正。 为了进行最小二乘线性回归，我们使用以下模型： $$ f_\hat{\theta}(x) = \hat{\theta} \cdot x $$ 我们通过最小化均方误差成本函数来拟合模型： $$ \begin{aligned} L(\hat{\theta}, X, y) &= \frac{1}{n} \sum_{i}^n(y_i - f_\hat{\theta} (X_i))^2\\ \end{aligned} $$ 在上述定义中，$x$表示$n 乘以 p$数据矩阵，$x$表示$x$的一行，$y$表示观察到的结果，$that \theta$表示模型权重。 ## 二级规范化定义 要将$L_2$正则化添加到模型中，我们修改上面的成本函数： $$ \begin{aligned} L(\hat{\theta}, X, y) &= \frac{1}{n} \sum_{i}(y_i - f_\hat{\theta} (X_i))^2 + \lambda \sum_{j = 1}^{p} \hat{\theta_j}^2 \end{aligned} $$ 请注意，上面的成本函数与前面的相同，加上$L_2$Regularization$\lambda\sum_j=1 ^ p \hat \theta_j ^2$term。本术语中的总和是每种型号重量的平方和，即$\Hat \Theta、\Hat \Theta、\Ldots、\Hat \Theta P。这个术语还引入了一个新的标量模型参数$\lambda$来调整正则化惩罚。 如果$\that \theta$中的值远离 0，正则化术语会导致成本增加。加入正则化后，最优模型权重将损失和正则化惩罚的组合最小化，而不是只考虑损失。由于得到的模型权重在绝对值上趋向于较小，因此该模型具有较低的方差和较高的偏差。 使用$l_2$正则化和线性模型以及均方误差成本函数，通常也被称为**岭回归**。 ### 正则化参数[¶](#The-Regularization-Parameter) 正则化参数$\lambda$控制正则化惩罚。一个小的$\lambda$会导致一个小的惩罚，如果$\lambda=0$正则化术语也是$0$并且成本根本没有正则化。 一个大的$\lambda$术语会导致一个大的惩罚，因此是一个更简单的模型。增加$\lambda$会减少方差并增加模型的偏差。我们使用交叉验证来选择$\lambda$的值，以最小化验证错误。 **关于`scikit-learn`中正则化的说明：** `scikit-learn`提供了内置正则化的回归模型。例如，要进行岭回归，可以使用[`sklearn.linear_model.Ridge`](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html)回归模型。注意，`scikit-learn`模型调用正则化参数`alpha`而不是$\lambda$。 `scikit-learn`方便地提供了规范化模型，这些模型执行交叉验证以选择一个好的值$\lambda$。例如，[`sklearn.linear_model.RidgeCV`](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RidgeCV.html#sklearn.linear_model.RidgeCV)允许用户输入正则化参数值，并自动使用交叉验证来选择验证错误最小的参数值。 ### 偏压项排除 注意，偏差项$\theta_$不包括在正则化项的总和中。我们不惩罚偏倚项，因为增加偏倚项不会增加模型的方差。偏倚项只会将所有预测值移动一个常量。 ### 数据规范化 注意，正则化术语$\lambda\sum_j=1 ^ p \that \theta ^2$对每个\theta j 2$的惩罚是相等的。但是，每个$\hat \theta j 的效果因数据本身而异。在添加 8 次多项式特征后，考虑水流数据集的这一部分： ``` # HIDDEN pd.DataFrame(clfs[2].named_steps['poly'].transform(X[:5]), columns=[f'deg_{n}_feat' for n in range(8)]) ``` | | deg_0_ 专长 | deg_1_ 专长 | …… | deg_6_ 专长 | deg_7_ 专长 | | --- | --- | --- | --- | --- | --- | | 零 | -15 | 二百五十三点九八 | …… | -261095791.08 元 | 4161020472.12 年 | | --- | --- | --- | --- | --- | --- | | 1 个 | -27.15 | 八百四十九点九零 | ... | -17897014961.65 | 521751305227.70 | | --- | --- | --- | --- | --- | --- | | 二 | 三十六点一九 | 1309.68 号 | ... | 81298431147.09 | 2942153527269.12 | | --- | --- | --- | --- | --- | --- | | 三 | 三十七点四九 | 1405.66 元 | ... | 104132296999.30 | 3904147586408.71 | | --- | --- | --- | --- | --- | --- | | 四 | -41.06 | 2309.65 美元 | ... | -592123531634.12 | 28456763821657.78 | | --- | --- | --- | --- | --- | --- | 5 行×8 列 我们可以看到 7 次多项式的特征值比 1 次多项式的特征值大得多。这意味着 7 级特征的大型模型权重对预测的影响远大于 1 级特征的大型模型权重。如果我们直接对这些数据应用正则化，正则化惩罚将不成比例地降低低阶特征的模型权重。在实际应用中，由于对预测影响较大的特征不受影响，即使采用正则化，也往往导致模型方差较大。 为了解决这个问题，我们 _ 通过减去平均值并将每一列中的值缩放到-1 和 1 之间来规范化 _ 每个数据列。在`scikit-learn`中，大多数回归模型允许使用`normalize=True`进行初始化，以便在拟合前规范化数据。 另一种类似的技术是 _ 标准化 _ 数据列，方法是减去平均值并除以每个数据列的标准偏差。 ## 使用岭回归 我们以前使用多项式特征来拟合 2、8 和 12 度多项式以获得水流数据。原始数据和结果模型预测在下面重复。 ``` # HIDDEN df ``` | | 水位变化 | 水流 | | --- | --- | --- | | 0 | -15.94 | 60422330445.52 号 | | --- | --- | --- | | 1 | -29.15 | 33214896575.60 元 | | --- | --- | --- | | 2 | 36.19 | 972706380901.06 | | --- | --- | --- | | ... | ... | ... 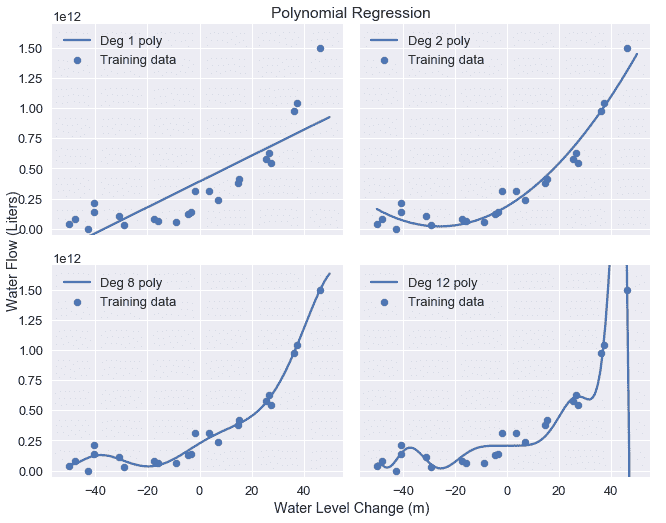| | --- | --- | --- | | 20 个 | 七点零九 | 236352046523.78 个 | | --- | --- | --- | | 21 岁 | 四十六点二八 | 149425638186.73 | | --- | --- | --- | | 二十二 | 十四点六一 | 378146284247.97 美元 | | --- | --- | --- | 23 行×2 列 ``` # HIDDEN plot_curves(curves) ```  为了进行岭回归，我们首先从数据中提取数据矩阵和结果向量： ``` X = df.iloc[:, [0]].as_matrix() y = df.iloc[:, 1].as_matrix() print('X: ') print(X) print() print('y: ') print(y) ``` ``` X: [[-15.94] [-29.15] [ 36.19] ... [ 7.09] [ 46.28] [ 14.61]] y: [6.04e+10 3.32e+10 9.73e+11 ... 2.36e+11 1.49e+12 3.78e+11] ``` 然后，我们对`X`应用 12 次多项式变换： ``` from sklearn.preprocessing import PolynomialFeatures # We need to specify include_bias=False since sklearn's classifiers # automatically add the intercept term. X_poly_8 = PolynomialFeatures(degree=8, include_bias=False).fit_transform(X) print('First two rows of transformed X:') print(X_poly_8[0:2]) ``` ``` First two rows of transformed X: [[-1.59e+01 2.54e+02 -4.05e+03 6.45e+04 -1.03e+06 1.64e+07 -2.61e+08 4.16e+09] [-2.92e+01 8.50e+02 -2.48e+04 7.22e+05 -2.11e+07 6.14e+08 -1.79e+10 5.22e+11]] ``` 我们指定了`scikit-learn`将使用交叉验证从中选择的`alpha`值，然后使用`RidgeCV`分类器来匹配转换的数据。 ``` from sklearn.linear_model import RidgeCV alphas = [0.01, 0.1, 1.0, 10.0] # Remember to set normalize=True to normalize data clf = RidgeCV(alphas=alphas, normalize=True).fit(X_poly_8, y) # Display the chosen alpha value: clf.alpha_ ``` ``` 0.1 ``` 最后，我们在正则化的 8 阶分类器旁边绘制基本 8 阶多项式分类器的模型预测： ``` # HIDDEN fig = plt.figure(figsize=(10, 5)) plt.subplot(121) plot_data() plot_curve(curves[2]) plt.title('Base degree 8 polynomial') plt.subplot(122) plot_data() plot_curve(ridge_curves[2]) plt.title('Regularized degree 8 polynomial') plt.tight_layout() ```  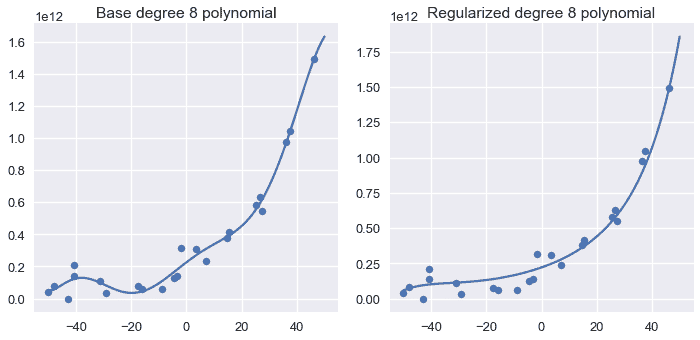我们可以看到，正则化多项式比基阶 8 多项式更平滑，并且仍然捕获了数据中的主要趋势。 比较非正则化和正则化模型的系数，发现岭回归有利于将模型权重放在较低阶多项式项上： ``` # HIDDEN base = coef_table(clfs[2]).rename(columns={'Coefficient Value': 'Base'}) ridge = coef_table(ridge_clfs[2]).rename(columns={'Coefficient Value': 'Regularized'}) pd.options.display.max_rows = 20 display(base.join(ridge)) pd.options.display.max_rows = 7 ``` | | 底座 | 正规化 | | --- | --- | --- | | 度 | | | | --- | --- | --- | | 0 | 225782472111.94 美元 | 221063525725.23 | | --- | --- | --- | | 1 | 13115217770.78 号 | 6846139065.96 美元 | | --- | --- | --- | | 2 | -144725749.98 美元 | 146158037.96 号 | | --- | --- | --- | | 3 | -10355082.91 元 | 193090.04 年 | | --- | --- | --- | | 4 | 567935.23 元 | 38240.62 元 | | --- | --- | --- | | 5 个 | 9805.14 年 | 五百六十四点二一 | | --- | --- | --- | | 六 | -249.64 条 | 七点二五 | | --- | --- | --- | | 七 | -2.09 | 零点一八 | | --- | --- | --- | | 8 个 | 零点零三 | 零 | | --- | --- | --- | 重复 12 次多项式特征的过程会得到类似的结果： ``` # HIDDEN fig = plt.figure(figsize=(10, 5)) plt.subplot(121) plot_data() plot_curve(curves[3]) plt.title('Base degree 12 polynomial') plt.ylim(-5e10, 170e10) plt.subplot(122) plot_data() plot_curve(ridge_curves[3]) plt.title('Regularized degree 12 polynomial') plt.ylim(-5e10, 170e10) plt.tight_layout() ```  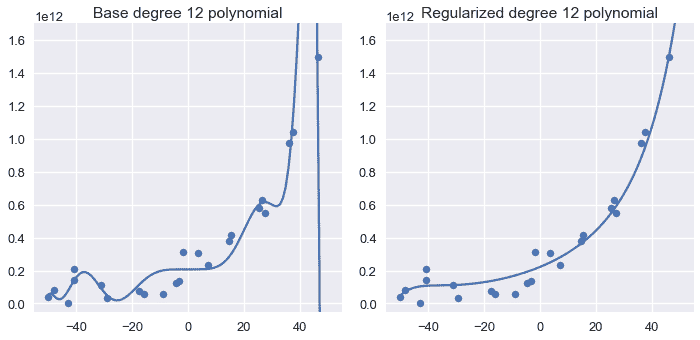增加正则化参数会使模型变得越来越简单。下图显示了将正则化量从 0.001 增加到 100.0 的效果。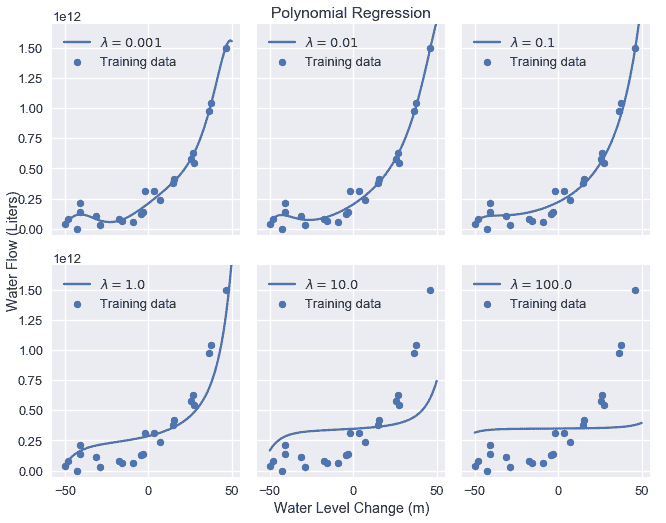 ``` # HIDDEN alphas = [0.001, 0.01, 0.1, 1.0, 10.0, 100.0] alpha_clfs = [Pipeline([ ('poly', PolynomialFeatures(degree=12, include_bias=False)), ('reg', Ridge(alpha=alpha, normalize=True))] ).fit(X, y) for alpha in alphas] alpha_curves = [make_curve(clf) for clf in alpha_clfs] labels = [f'$\\lambda = {alpha}$' for alpha in alphas] plot_curves(alpha_curves, cols=3, labels=labels) ```  如我们所见，增加正则化参数会增加模型的偏差。如果我们的参数太大，模型就会变成一个常量模型，因为任何非零的模型权重都会受到严重惩罚。 ## 摘要[¶](#Summary) 使用$L_2$正则化可以通过惩罚大型模型权重来调整模型偏差和方差。$L_2$最小二乘线性回归的正则化也被更常见的名称岭回归所知。使用正则化添加了一个额外的模型参数$\lambda$，我们使用交叉验证进行调整。