# 使用逻辑回归 > 原文：[https://www.textbook.ds100.org/ch/17/classification_log_reg.html](https://www.textbook.ds100.org/ch/17/classification_log_reg.html) ``` # HIDDEN # Clear previously defined variables %reset -f # Set directory for data loading to work properly import os os.chdir(os.path.expanduser('~/notebooks/17')) ``` ``` # HIDDEN import warnings # Ignore numpy dtype warnings. These warnings are caused by an interaction # between numpy and Cython and can be safely ignored. # Reference: https://stackoverflow.com/a/40846742 warnings.filterwarnings("ignore", message="numpy.dtype size changed") warnings.filterwarnings("ignore", message="numpy.ufunc size changed") import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns %matplotlib inline import ipywidgets as widgets from ipywidgets import interact, interactive, fixed, interact_manual import nbinteract as nbi sns.set() sns.set_context('talk') np.set_printoptions(threshold=20, precision=2, suppress=True) pd.options.display.max_rows = 7 pd.options.display.max_columns = 8 pd.set_option('precision', 2) # This option stops scientific notation for pandas # pd.set_option('display.float_format', '{:.2f}'.format) ``` ``` # HIDDEN def df_interact(df, nrows=7, ncols=7): ''' Outputs sliders that show rows and columns of df ''' def peek(row=0, col=0): return df.iloc[row:row + nrows, col:col + ncols] if len(df.columns) <= ncols: interact(peek, row=(0, len(df) - nrows, nrows), col=fixed(0)) else: interact(peek, row=(0, len(df) - nrows, nrows), col=(0, len(df.columns) - ncols)) print('({} rows, {} columns) total'.format(df.shape[0], df.shape[1])) ``` ``` # HIDDEN from scipy.optimize import minimize as sci_min def minimize(cost_fn, grad_cost_fn, X, y, progress=True): ''' Uses scipy.minimize to minimize cost_fn using a form of gradient descent. ''' theta = np.zeros(X.shape[1]) iters = 0 def objective(theta): return cost_fn(theta, X, y) def gradient(theta): return grad_cost_fn(theta, X, y) def print_theta(theta): nonlocal iters if progress and iters % progress == 0: print(f'theta: {theta} | cost: {cost_fn(theta, X, y):.2f}') iters += 1 print_theta(theta) return sci_min( objective, theta, method='BFGS', jac=gradient, callback=print_theta, tol=1e-7 ).x ``` 我们已经开发了逻辑回归的所有组件。首先，用于预测概率的逻辑模型： $$ \begin{aligned} f_\hat{\boldsymbol{\theta}} (\textbf{x}) = \sigma(\hat{\boldsymbol{\theta}} \cdot \textbf{x}) \end{aligned} $$ 然后，交叉熵损失函数： $$ \begin{aligned} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) = &= \frac{1}{n} \sum_i \left(- y_i \ln \sigma_i - (1 - y_i) \ln (1 - \sigma_i ) \right) \\ \end{aligned} $$ 最后，梯度下降的交叉熵损失的梯度： $$ \begin{aligned} \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) &= - \frac{1}{n} \sum_i \left( y_i - \sigma_i \right) \textbf{X}_i \\ \end{aligned} $$ 在上面的表达式中，我们让$\textbf \x；$表示 p$输入数据矩阵的$n 乘以 p$输入值，$\textbf \123\ \，$\textbf \，$\textbf \123\123 123 123 123 123 \ 123 \ \123 \\\\Thet 公司 A 美元。简而言之，我们定义了$\sigma \boldsymbol \theta（\textbf x u i）=\sigma（\textbf x u i \cdot \hat \boldsymbol \theta）。 ## 勒布朗射门的逻辑回归 现在让我们回到本章开头所面临的问题：预测勒布朗·詹姆斯将要投哪一球。我们从加载勒布朗在 2017 年 NBA 季后赛中拍摄的照片开始。 ``` lebron = pd.read_csv('lebron.csv') lebron ``` | | 游戏日期 | 分钟 | 对手 | 动作类型 | 镜头类型 | 射击距离 | 拍摄 | | --- | --- | --- | --- | --- | --- | --- | --- | | 零 | 20170415 年 | 10 个 | 因德 | 驾驶上篮得分 | 2pt 现场目标 | 零 | 0 | | --- | --- | --- | --- | --- | --- | --- | --- | | 1 个 | 20170415 | 11 个 | IND | Driving Layup Shot | 2PT Field Goal | 0 | 1 个 | | --- | --- | --- | --- | --- | --- | --- | --- | | 二 | 20170415 | 十四 | IND | 上篮得分 | 2PT Field Goal | 0 | 1 | | --- | --- | --- | --- | --- | --- | --- | --- | | …… | …… | ... | ... | ... | ... | ... | ... | | --- | --- | --- | --- | --- | --- | --- | --- | | 三百八十一 | 20170612 年 | 46 岁 | GSW | Driving Layup Shot | 2PT Field Goal | 1 | 1 | | --- | --- | --- | --- | --- | --- | --- | --- | | 382 个 | 20170612 | 47 岁 | GSW | 后仰跳投 | 2PT Field Goal | 14 | 0 | | --- | --- | --- | --- | --- | --- | --- | --- | | 三百八十三 | 20170612 | 48 岁 | GSW | Driving Layup Shot | 2PT Field Goal | 二 | 1 | | --- | --- | --- | --- | --- | --- | --- | --- | 384 行×7 列 我们在下面包含了一个小部件，允许您浏览整个数据帧。 ``` df_interact(lebron) ``` <button class="js-nbinteract-widget">Loading widgets...</button> ``` (384 rows, 7 columns) total ``` 我们首先只使用拍摄距离来预测拍摄是否进行。`scikit-learn`方便地提供了一个逻辑回归分类器作为[`sklearn.linear_model.LogisticRegression`](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html)类。为了使用这个类，我们首先创建数据矩阵`X`和观察结果向量`y`。 ``` X = lebron[['shot_distance']].as_matrix() y = lebron['shot_made'].as_matrix() print('X:') print(X) print() print('y:') print(y) ``` ``` X: [[ 0] [ 0] [ 0] ... [ 1] [14] [ 2]] y: [0 1 1 ... 1 0 1] ``` 按照惯例，我们将数据分成一个训练集和一个测试集。 ``` from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=40, random_state=42 ) print(f'Training set size: {len(y_train)}') print(f'Test set size: {len(y_test)}') ``` ``` Training set size: 344 Test set size: 40 ``` `scikit-learn`使初始化分类器并将其安装在`X_train`和`y_train`上变得简单： ``` from sklearn.linear_model import LogisticRegression simple_clf = LogisticRegression() simple_clf.fit(X_train, y_train) ``` ``` LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1, penalty='l2', random_state=None, solver='liblinear', tol=0.0001, verbose=0, warm_start=False) ``` 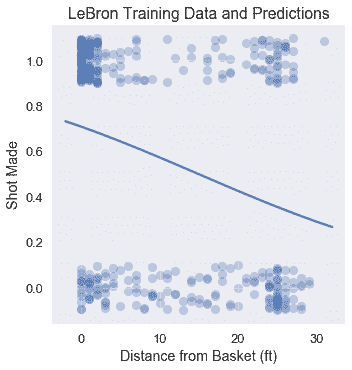为了可视化分类器的性能，我们绘制了原始点和分类器的预测概率。 ``` # HIDDEN np.random.seed(42) sns.lmplot(x='shot_distance', y='shot_made', data=lebron, fit_reg=False, ci=False, y_jitter=0.1, scatter_kws={'alpha': 0.3}) xs = np.linspace(-2, 32, 100) ys = simple_clf.predict_proba(xs.reshape(-1, 1))[:, 1] plt.plot(xs, ys) plt.title('LeBron Training Data and Predictions') plt.xlabel('Distance from Basket (ft)') plt.ylabel('Shot Made'); ```  ## 正在评估分类器[¶](#Evaluating-the-Classifier) 评估分类器有效性的一种方法是检查其预测精度：它正确预测的点数比例是多少？ ``` simple_clf.score(X_test, y_test) ``` ``` 0.6 ``` 我们的分类器在测试集上实现了相当低的精度 0.60。如果我们的分类器只是随机地猜测每个点，那么我们期望精度为 0.50。事实上，如果我们的分类器简单地预测到 Lebron 的每一次射门都会成功，我们也会得到 0.60 的准确度： ``` # Calculates the accuracy if we always predict 1 np.count_nonzero(y_test == 1) / len(y_test) ``` ``` 0.6 ``` 对于这个分类器，我们只使用了几个可能的特性中的一个。在多变量线性回归中，我们可能通过合并更多的特征来实现更精确的分类器。 ## 多变量逻辑回归 在我们的分类器中合并更多的数字特性就如同从`lebron`数据帧中提取额外的列到`X`矩阵中一样简单。另一方面，结合分类特征需要我们应用一个热编码。在下面的代码中，我们使用`minute`、`opponent`、`action_type`和`shot_type`功能增强了分类器，使用`scikit-learn`中的`DictVectorizer`类对分类变量应用一个热编码。 ``` from sklearn.feature_extraction import DictVectorizer columns = ['shot_distance', 'minute', 'action_type', 'shot_type', 'opponent'] rows = lebron[columns].to_dict(orient='row') onehot = DictVectorizer(sparse=False).fit(rows) X = onehot.transform(rows) y = lebron['shot_made'].as_matrix() X.shape ``` ``` (384, 42) ``` 我们将再次将数据分为训练集和测试集： ``` X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=40, random_state=42 ) print(f'Training set size: {len(y_train)}') print(f'Test set size: {len(y_test)}') ``` ``` Training set size: 344 Test set size: 40 ``` 最后，我们再次调整模型并检查其准确性： ``` clf = LogisticRegression() clf.fit(X_train, y_train) print(f'Test set accuracy: {clf.score(X_test, y_test)}') ``` ``` Test set accuracy: 0.725 ``` 这个分类器比只考虑射击距离的分类器精确 12%左右。在第 17.7 节中，我们探讨了用于评估分类器性能的其他指标。 ## 摘要[¶](#Summary) 我们开发了使用逻辑回归进行分类所需的数学和计算机制。逻辑回归因其预测简单有效而得到广泛应用。