从本讲开始将进入数据结构的全新篇章：哈希表。若要构建出哈希表这种数据结构的话，会涉及到两个重要的算法，分别是哈希函数和解决哈希碰撞的算法。在接下来的第 05 和 06 讲中，我们会先一起研究哈希函数的本质以及它的应用；在第 07 和 08 讲中，将会探讨当遇到哈希碰撞时应该如何解决，以及哈希表在实战中的应用。 #### 哈希表与哈希函数 说到哈希表，其实本质上是一个数组。通过前面的学习我们知道了，如果要访问一个数组中某个特定的元素，那么需要知道这个元素的索引。例如，我们可以用数组来记录自己好友的电话号码，索引 0 指向的元素记录着 A 的电话号码，索引 1 指向的元素记录着 B 的电话号码，以此类推。 而当这个数组非常大的时候，全凭记忆去记住哪个索引记录着哪个好友的号码是非常困难的。这时候如果有一个函数，可以将我们好友的姓名作为一个输入，然后输出这个好友的号码在数组中对应的索引，是不是就方便了很多呢？这样的一种函数，其实就是哈希函数。哈希函数的定义是将任意长度的一个对象映射到一个固定长度的值上，而这个值我们可以称作是哈希值（Hash Value）。 哈希函数一般会有以下三个特性： * 任何对象作为哈希函数的输入都可以得到一个相应的哈希值； * 两个相同的对象作为哈希函数的输入，它们总会得到一样的哈希值； * 两个不同的对象作为哈希函数的输入，它们不一定会得到不同的哈希值。 对于哈希函数的前两个特性，比较好理解，但是对于第三种特性，我们应该如何解读呢？那下面就通过一个例子来说明。 我们按照 Java String 类里的哈希函数公式（即下面的公式）来计算出不同字符串的哈希值。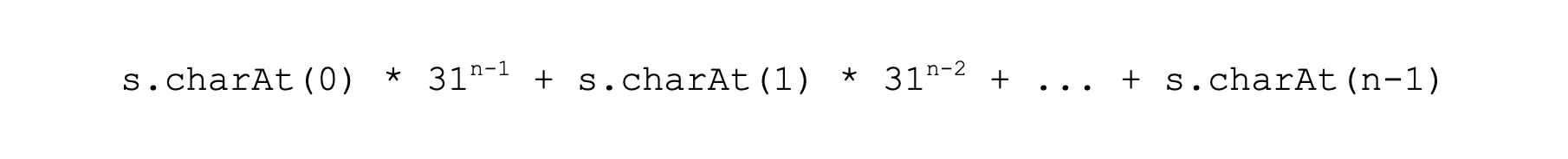String 类里的哈希函数是通过 hashCode 函数来实现的，这里假设哈希函数的字符串输入为 s，所有的字符串都会通过以下公式来生成一个哈希值：  > 这里为什么是“31”？下面会讲到哦~ 注意：下面所有字符的数值都是按照 ASCII 表获得的，具体的数值可以在这里查阅。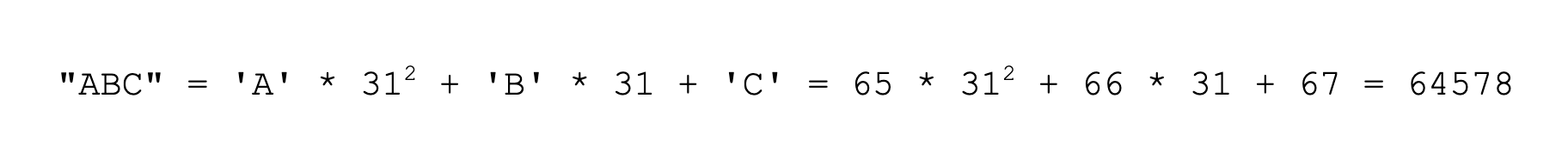 如果我们输入“ABC”这个字符串，那根据上面的哈希函数公式，它的哈希值则为  在什么样的情况下会体现出哈希函数的第三种特性呢？我们再来看看下面这个例子。现在我们想要计算字符串 "Aa" 和 "BB" 的哈希值，还是继续套用上面的的公式。 "Aa" 的哈希值为 ``` "Aa" = 'A' * 31 + 'a' = 65 * 31 + 97 = 2112 ``` "BB" 的哈希值为： ``` "BB" = 'B' * 31 + 'B' = 66 * 31 + 66 = 2112 ``` 可以看到，不同的两个字符串其实是会输出相同的哈希值出来的，这时候就会造成哈希碰撞，具体的解决方法将会在第 07 讲中详细讨论。 需要注意的是，虽然 hashCode 的算法里都是加法，但是算出来的哈希值有可能会是一个负数。 我们都知道，在计算机里，一个 32 位 int 类型的整数里最高位如果是 0 则表示这个数是非负数，如果是 1 则表示是负数。 如果当字符串通过计算算出的哈希值大于 232-1 时，也就是大于 32 位整数所能表达的最大正整数了，则会造成溢出，此时哈希值就变为负数了。感兴趣的小伙伴可以按照上面的公式，自行计算一下“19999999999999999”这个字符串的哈希值会是多少。 * [ ] hashCode 函数中的“魔数”（Magic Number） 细心的你一定发现了，上面所讲到的 Java String 类里的 hashCode 函数，一直在使用一个 31 这样的正整数来进行计算，这是为什么呢？下面一起来研究一下 Java Openjdk-jdk11 中 String.java 的源码（源码链接），看看这么做有什么好处。 ``` public int hashCode() {     int h = hash;     if (h == 0 && value.length > 0) {         hash = h = isLatin1() ? StringLatin1.hashCode(value)                               : StringUTF16.hashCode(value);     }     return ``` 可以看到，String 类的 hashCode 函数依赖于 StringLatin1 和 StringUTF16 类的具体实现。而 StringLatin1 类中的 hashCode 函数（源码链接）和 StringUTF16 类中的 hashCode 函数（源码链接）所表达的算法其实是一致的。 StringLatin1 类中的 hashCode 函数如下面所示： ``` public static int hashCode(byte[] value) {     int h = 0;     for (byte v : value) {         h = 31 * h + (v & 0xff);     }     return h ``` StringUTF16 类中的 hashCode 函数如下面所示： ``` public static int hashCode(byte[] value) {     int h = 0;     int length = value.length >> 1;     for (int i = 0; i < length; i++) {         h = 31 * h + getChar(value, i);     }     return h ``` 一个好的哈希函数算法都希望尽可能地减少生成出来的哈希值会造成哈希碰撞的情况。 Goodrich 和 Tamassia 这两位计算机科学家曾经做过一个实验，他们对超过 50000 个英文单词进行了哈希值运算，并使用常数 31、33、37、39 和 41 作为乘数因子，每个常数所算出的哈希值碰撞的次数都小于 7 个。但是最终选择 31 还是有着另外几个原因。 从数学的角度来说，选择一个质数（Prime Number）作为乘数因子可以让哈希碰撞减少。其次，我们可以看到在上面的两个 hashCode 源码中，都有着一条 31 * h 的语句，这条语句在 JVM 中其实都可以被自动优化成“(h << 5) - h”这样一条位运算加上一个减法指令，而不必执行乘法指令了，这样可以大大提高运算哈希函数的效率。 所以最终 31 这个乘数因子就被一直保留下来了。 * [ ] 区块链挖矿的本质 通过上面的学习，相信你已经对哈希函数有了一个比较好的了解了。可能也发现了，哈希函数从输入到输出，我们可以按照函数的公式算法，很快地计算出哈希值。但是如果告诉你一个哈希值，即便给出了哈希函数的公式也很难算得出原来的输入到底是什么。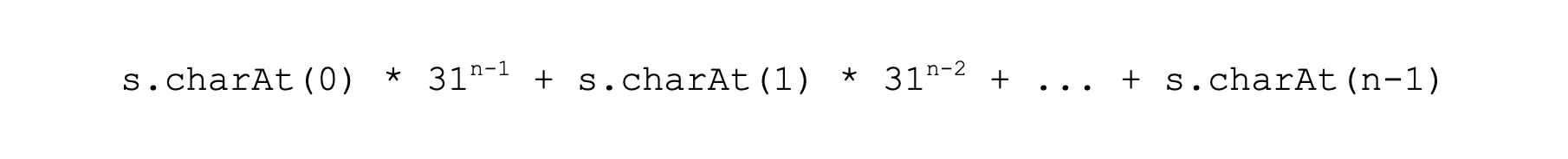例如，还是按照上面 String 类的 hashCode 函数的计算公式：  如果告诉了你哈希值是 123456789 这个值，那输入的字符串是什么呢？我们想要知道答案的话，只能采用暴力破解法，也就是一个一个的字符串去尝试，直到尝试出这个哈希值为止。 对于区块链挖矿来说，这个“矿”其实就是一个字符串。“矿工”，也就是进行运算的计算机，必须在规定的时间内找到一个字符串，使得在进行了哈希函数运算之后得到一个满足要求的值。 我们以比特币为例，它采用了 SHA256 的哈希函数来进行运算，无论输入的是什么，SHA256 哈希函数的哈希值永远都会是一个 256 位的值。而比特币的奖励机制简单来说是通过每 10 分钟放出一个哈希值，让“矿工们”利用 SHA256(SHA256(x)) 这样两次的哈希运算，来找出满足一定规则的字符串出来。 比方说，比特币会要求找出通过上面 SHA256(SHA256(x)) 计算之后的哈希值，这个 256 位的哈希值中的前 50 位都必须为 0 ，谁先找到满足这个要求的输入值 x，就等于“挖矿”成功，给予奖励一个比特币。我们知道，即便知道了哈希值，也很难算出这个 x 是什么，所以只能一个一个地去尝试。而市面上所说的挖矿机，其原理是希望能提高运算的速度，让“矿工”尽快地找到这个 x 出来。