在经过了前面 16 个课时的学习之后，我们已经将所有的基础数据结构都学习了一遍。由于每个数据结构都有自身的优缺点，所以在实际应用的时候，我们应该先了解应用场景的需求。比如说，一个需要频繁删改数据的场景和只是频繁添加和读取数据的场景，我们所选取的数据结构是不尽相同的。然而，当想要弥补一个数据结构其中的短板时，往往会通过结合另外一种数据结构，来实现取长补短。 在今天这一课时中，我将着重介绍在业界中的几个常见应用，它们都是将几个不同的基础数据结构结合起来，从而打出一套漂亮的数据结构“组合拳”。 #### LRU 缓存 LRU 缓存是利用了 Least Recently Used 算法来实现的一种最最常见的缓存策略。LRU 算法其实不单单只是在缓存策略中被大量用到，它还在计算机操作系统的内存管理中也是一种常见的策略。下面我们先来介绍一下什么是 LRU 算法。 假设有一个应用希望能够加快数据的访问速度，因此在内存中设置了缓存来进行加速，为了方便说明，我们假设内存中只能够存储 3 个数据，当有更新的数据需要保存在缓存中时，我们必须按照 LRU 算法把最老的数据剔除掉。 当访问第一个数据 A 的时候，因为缓存中还没有任何数据，所以可以直接将 A 放到缓存中。如下图所示：  紧接着应用又访问了 B 和 C，我们按照从左到右由新到旧的顺序来表示缓存中存储的数据，如下图所示：  也就是说在最左边的数据 C 是我们最新放入缓存中的数据，最右边的 A 是我们最早放入缓存中的数据。 当应用需要再次访问 A 的时候，应用不需要去硬盘中读取了，可以直接从缓存中读取，而此时的缓存如下图所示，也就是说，数据 B 变成了最早访问的数据：  此时，应用需要访问数据 D，而缓存中已经保存满了 3 个数据，我们必须将最老的数据剔除，也就是剔除掉 B。现在的缓存如下图所示：  好了，LRU 的算法其实理解起来不算困难，整个算法需要有以下几个操作： * Get 操作用于获取相应的数据； * Remove 操作将一个数据从缓存中删除； * Set 操作用于将相应的数据存放在缓存中，如果缓存空间并未满，则将数据直接存入缓存；如果缓存空间已满，则调用 Remove 操作将最旧的数据从缓存中删除，然后再将新数据存放在缓存中。 那我们要选择哪一种数据结构来表达这个算法好呢？ 因为 LRU 算法里有 Get、Set 和 Remove 操作，所以你很快就想到了哈希表这个数据结构，对于哈希表来说，这些操作的时间复杂度是 O(1)。但哈希表的缺点是无法知道数据插入的顺序，这样我们也就无法得知哪个数据是最新的、哪个数据是最旧的。 那链表也许是一个不错的选择，我们可以维护一个头节点指向缓存中最新的数据，尾节点指向缓存中最老的数据。当需要添加新数据而缓存还没有满的时候，可以直接将数据添加到链表头，但这里有一个问题，我们要如何判断这个新数据已经存在于缓存中了呢？需要遍历一遍整个链表，其所需的时间复杂度是 O(N)。 同理，Get 和 Remove 操作同样需要遍历整个链表，平均下来时间复杂度也是 O(N)。这样，我们虽然解决了维护一个从最新使用到最旧的数据问题，但是时间复杂度却提高了。 #### 哈希表和链表的结合 最终的解决方法也许你已经想到了，就是将哈希表和链表结合起来，哈希表的值保存了链表节点的位置。因为我们需要记录数据的使用情况，一个常见的操作是将链表中某一个节点数据移动至链表头，所以在这里采用双向链表，从而可以更方便地将链表中的数据移动至链表头。哈希表的作用是可以使查找一个数据的时间复杂度降到 O(1)。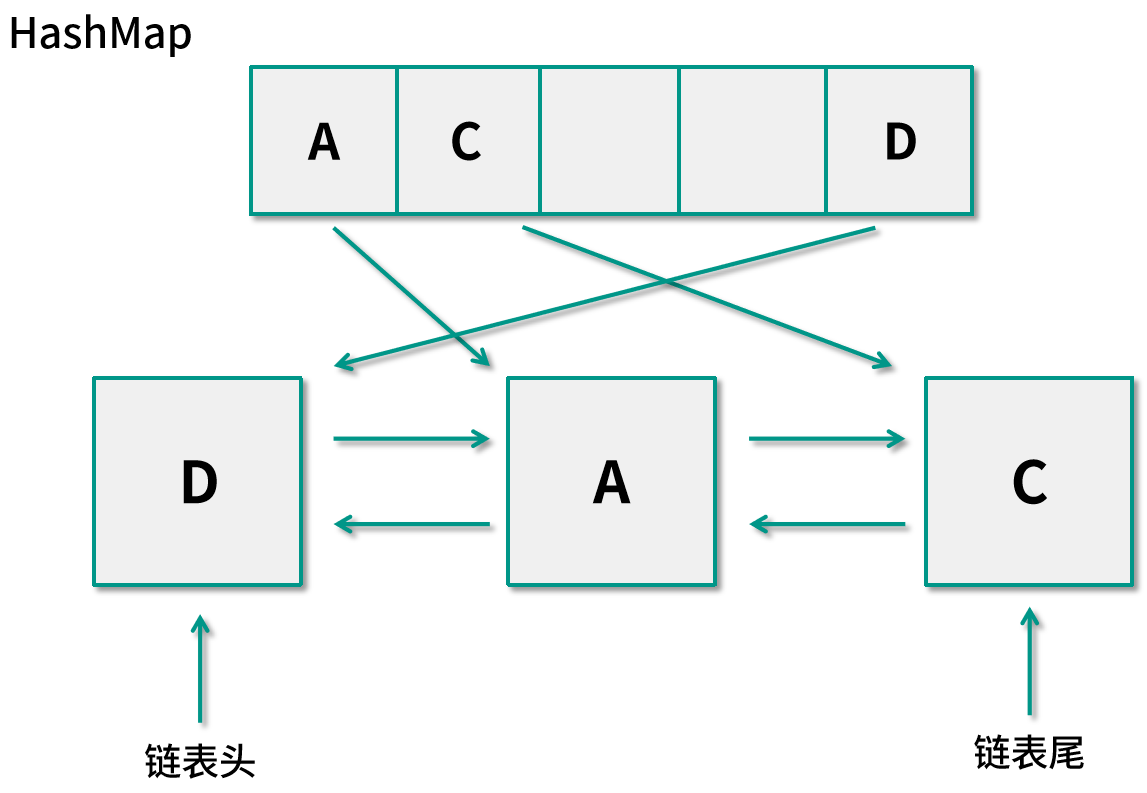 这个时候，缓存的内存图如下图所示：   我们来再举例说明一下几个关键操作在融合了哈希表和双向链表后的时间复杂度。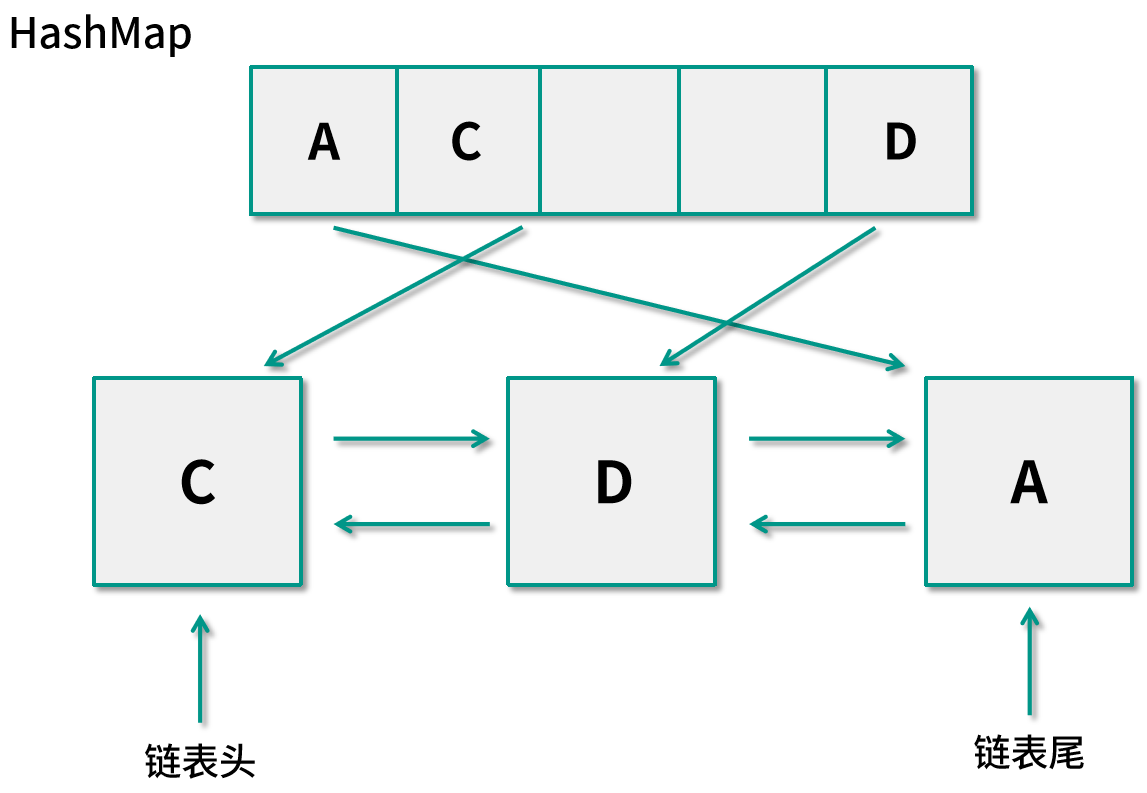 假设应用再次需要访问数据 C，我们需要先判断缓存中是否已经保存过这个数据了，此时只需要从哈希表中查看，发现 C 已经存在，通过哈希表的值我们可以直接定位到 C 节点在链表中的位置，再将这个节点移动到双向链表的链表头，这个操作的时间复杂度为 O(1)，内存图如下所示：  如果应用需要访问数据 B，我们还是需要判断缓存中是否已经保存过这个数据了，通过哈希表可以发现并不存在，而缓存中的数据已经满了，所以需要剔除最旧的数据 A，也就是保存在双向链表链表尾的节点。因为维护了尾节点，我们可以在 O(1) 的时间内找到它，同时将哈希表中的数据也删除掉。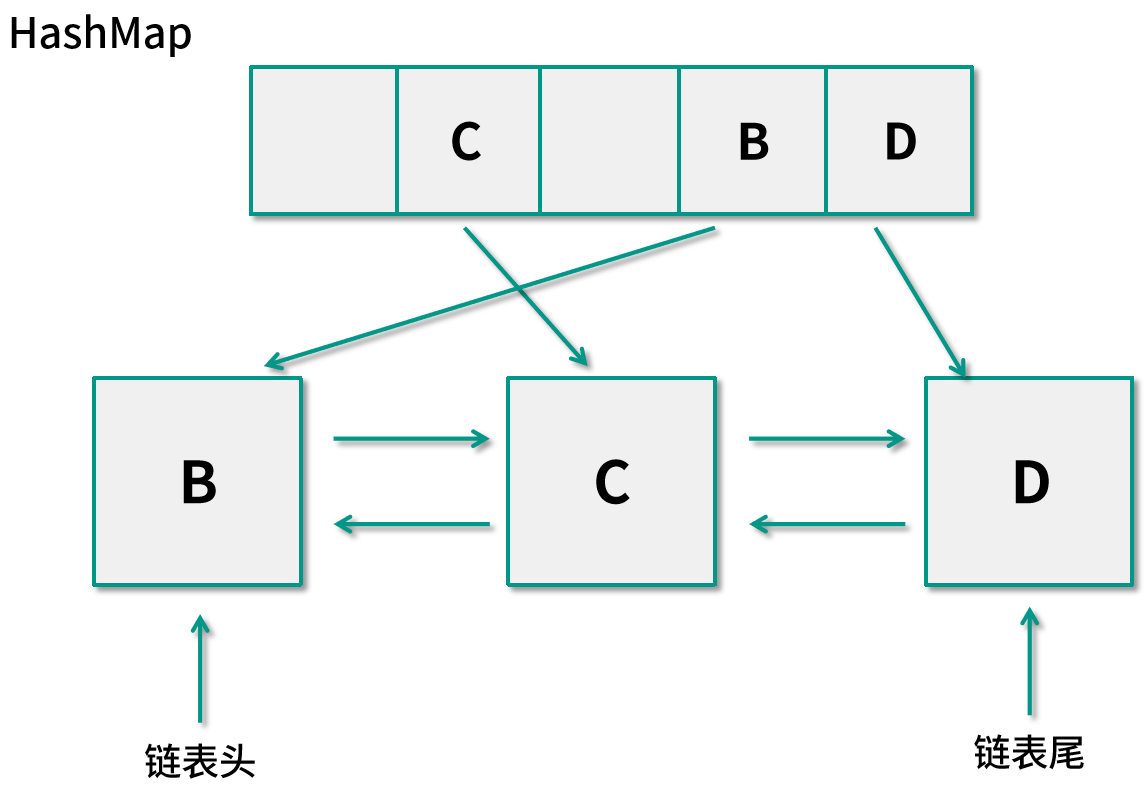现在的尾节点则指向了 D，而链表头则指向了新加入的节点 B，内存如下图所示：  这样的数据结构组合可以将所有的操作时间复杂度都优化到了 O(1)，像 Memcached 和 Nginx 这样反向代理都会使用这种 LRU 算法。 当然了，如果你是使用 Java 的话，应该听说过一个叫 LinkedHashMap 的 Collection，它的核心实现部分其实和上面讲到的哈希表与链表的结合很像，感兴趣的话可以自行研究一下它的实现方式。(点击这里查看源代码) #### Trie 树 这里我还想和你介绍另外一个高级数据结构，那就是 Trie 树。Trie 树也被称为前缀树或者字典树，下面我们通过一个例子来说明一下 Trie 树的优点。 我们希望能够快速插入并且查找一系列的字符串，比如说以下的字符串：String、Stringent、Strings、Strong，当然了，使用哈希表来达到这个要求是毫无问题的。但是如果现在我们再额外加一些限制，比如说要存储的字符串不单单是正常的英文单词，还可以是十分长的无规则的字符串，在内存空间也十分有限的情况下，我们要如何应对呢？这个时候 Trie 树就派上用场了。 以上面的 4 个字符串为例，其实它们都有着一些相同的前缀，比如说 String、Stringent，Strings 有 String 这样的相同前缀，String、Stringent、Strings、Strong 有 Str 这样的相同前缀。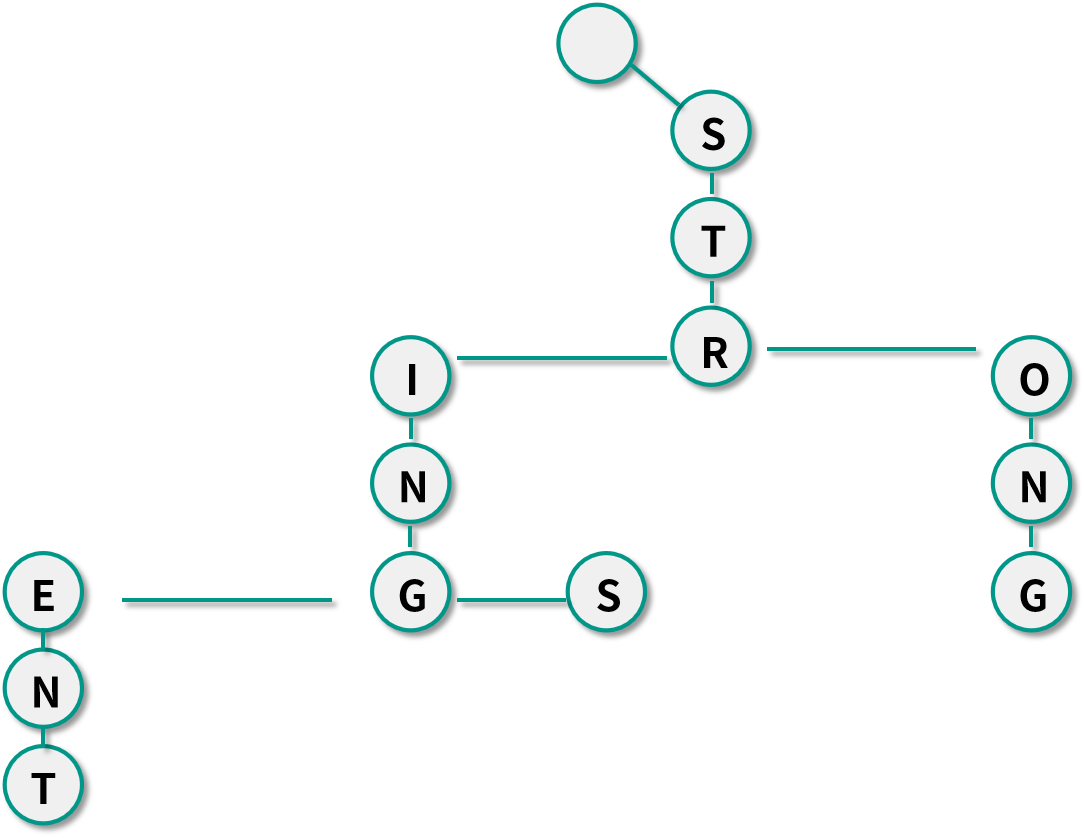我们可以通过 Trie 树来优化存储空间，使不同的字符串尽量共享相同的前缀，一个根据上面 4 个字符串构建出来的 Trie 树，如下图所示：  根据这种思想，在插入一个字符串的时候，会按照字母顺序将每一个字母作为 Trie 树的节点保存起来。在查找字符串是否存在的时候，只需要顺着 Trie 树的根节点从上至下往下搜索便可了。当然了，Trie 树的每一个节点可以不单单保存一个字母，可以根据应用的需求来增加其他的值。 Trie 树的应用十分广泛，比如说常见的 DNS 反向解析，也就是通过一个 IP 地址到域名的解析，同样会用到 Trie 树。因为 IP 地址从理论上，每一部分都是由 0 到 255 组成的，这里面有着相当多的共同前缀，如果使用 Trie 树来进行 DNS 反向解析的话，则可以节省大量的内存空间。