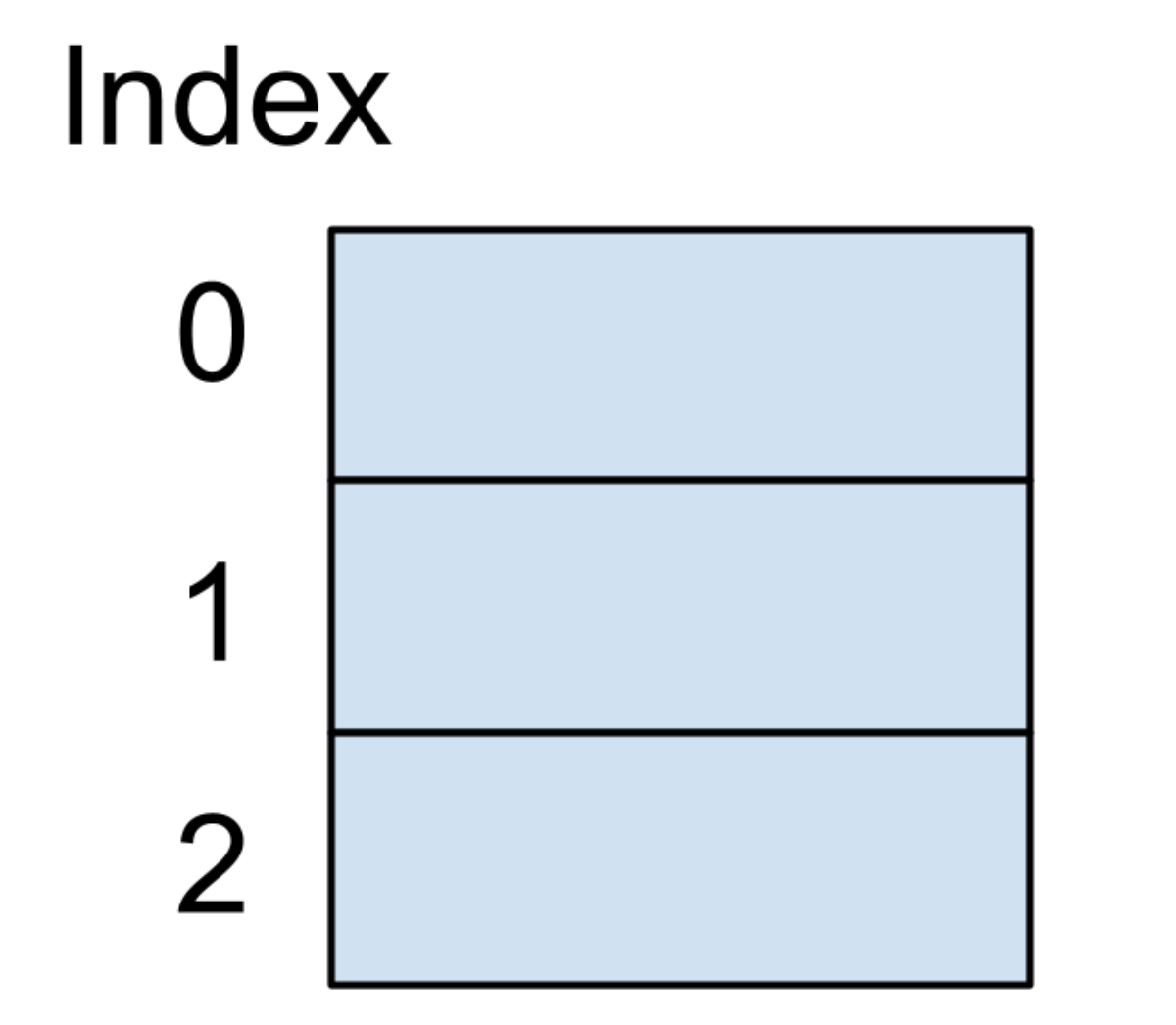
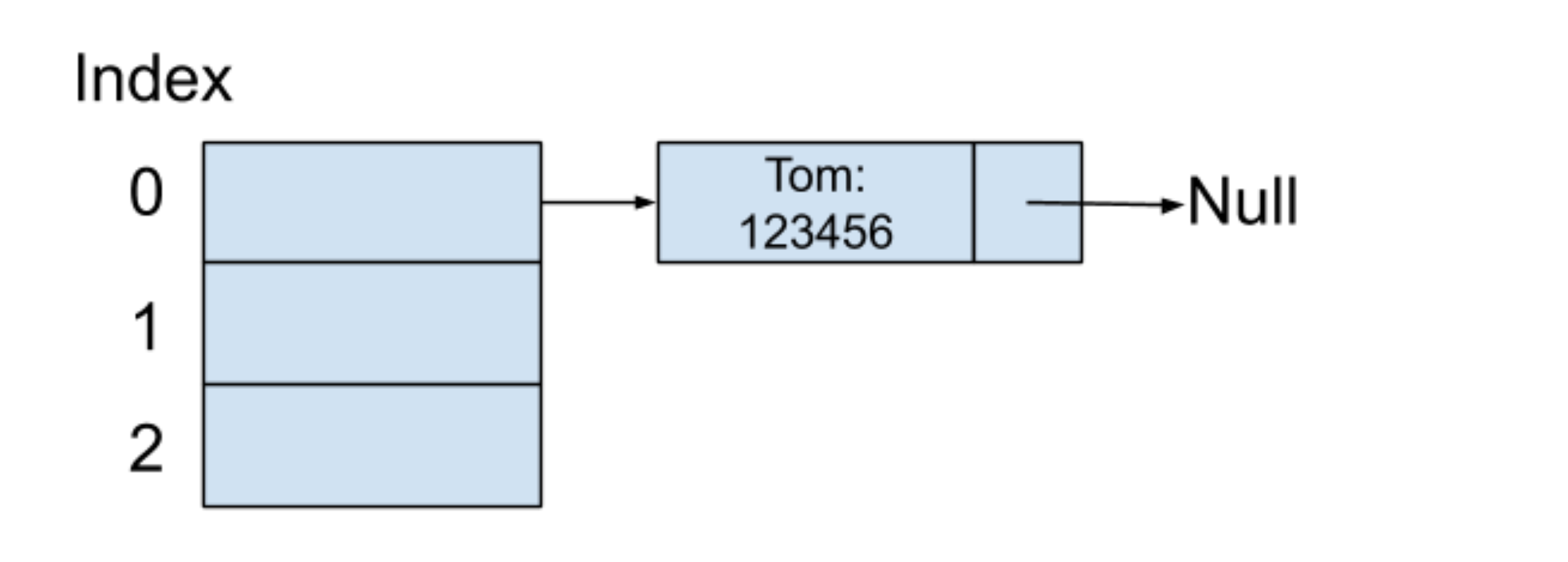
通过前两讲的学习，相信你已经清楚地理解了哈希函数的概念以及它的应用了，那么这一讲我们一起学习一下，通过哈希函数产生了哈希碰撞，应该如何处理？在学习完哈希碰撞的解决方式之后，我们就可以完整地认识哈希表这种数据结构了。最后，我会带你来了解一个哈希表的常用高级应用——BloomFilter。 #### 哈希碰撞的情况 先来看看哈希表的定义，在概念上哈希表可以定义为是一个根据键（Key）而直接访问在内存中存储位置的值（Value）的数据结构。这里所说的键就是指哈希函数的输入，而这里的值并不是指哈希值，而是指我们想要保存的值。 在现实中， 想要有一个完美的哈希函数，将输入值转换成哈希值而不产生哈希碰撞基本是不可能的，所以哈希表在通过键来访问存储位置的值的时候，是根据我们处理哈希碰撞来决定它自身操作的。那下面我们就以一个具体例子来说明一下，不同的哈希碰撞其解决方式所带来的底层存储键值对操作的差异。 我们假设存储哈希表的底层数据结构是一个大小为 3 的数组，我们还是以保存好友电话号码为例，这个哈希表的键是我们好友的名字，哈希表的值是这个好友的电话号码。刚开始的时候，因为这个数据结构并没有存储任何信息，所以数据结构内存结构图如下图所示：  假设第一个输入的键值对是（Tom：123456），表示好友的名字叫 Tom，电话号码为 123456。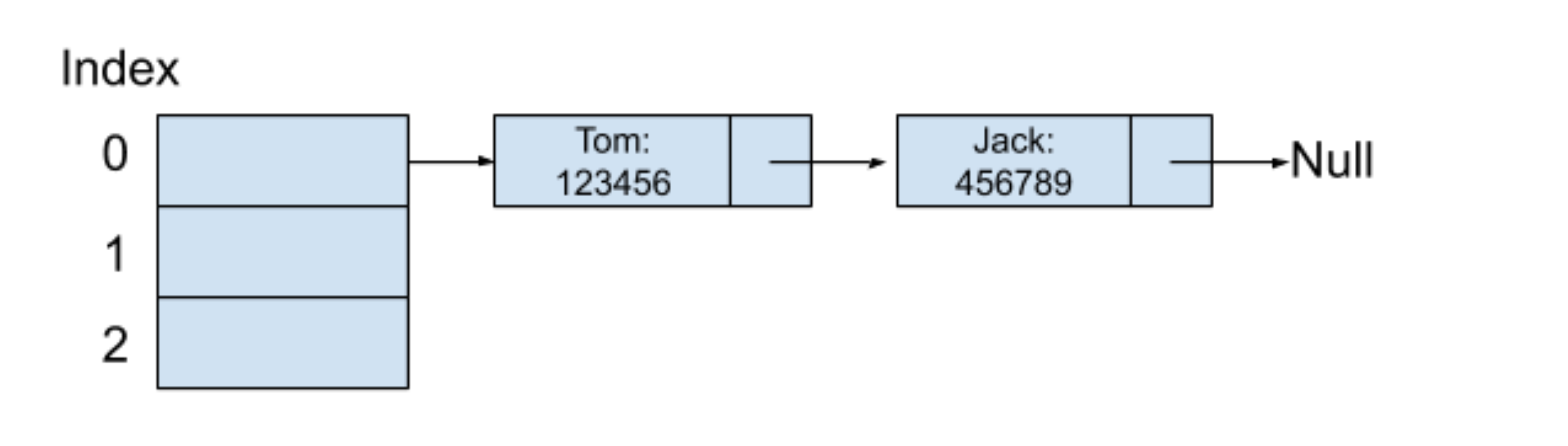我们同时假设 Tom 这个字符串在通过哈希函数之后的所产生的哈希值是 0，此时可以把 123456 这个值放在以哈希值为索引的地方，内存结构如下图所示：  紧接着，我们输入的第二个键值对是（Jack：456789），同时假设 Jack 这个字符串在通过哈希函数之后的所产生的哈希值也是 0，而因为索引为 0 的位置已经存放一个值了，也就表示这时候产生了哈希碰撞。下面我就介绍一下常用的两种解决哈希碰撞的方式。 * [ ] 开放寻址法（Open Addressing） 开放寻址法本质上是在数组中寻找一个还未被使用的位置，将新的值插入。这样做的好处是利用数组原本的空间而不用开辟额外的空间来保存值。最简单明了的方法就是沿着数组索引，往下一个一个地去寻找还未被使用的空间，这种方法叫做线性探测（Linear Probing）。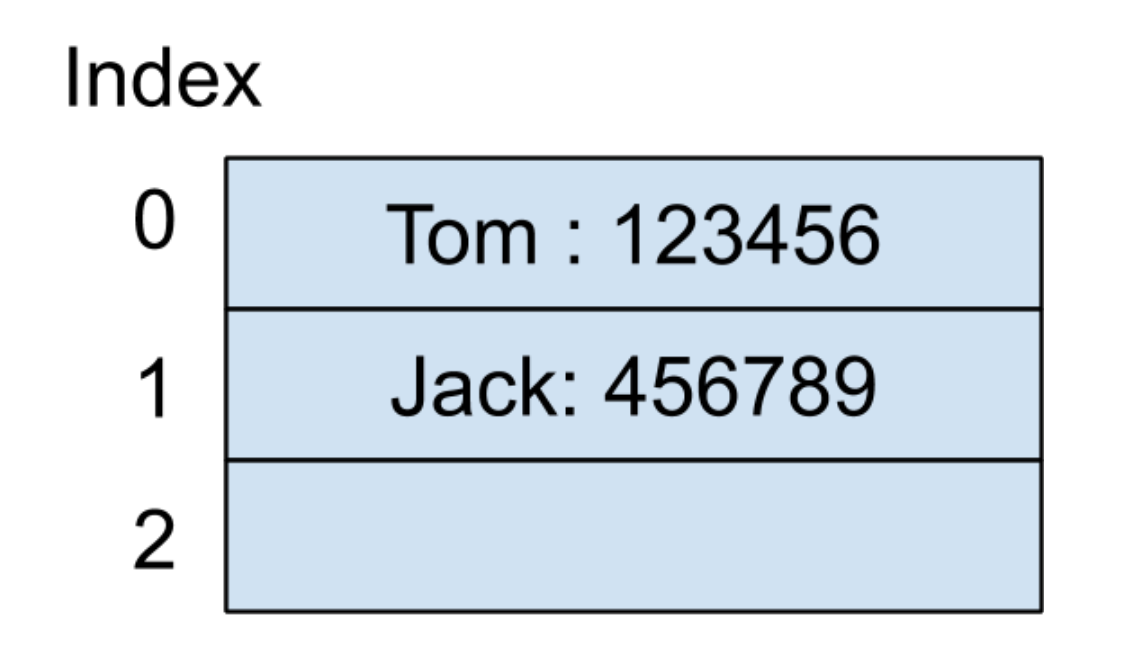 继续看刚才的例子，因为索引为 0 的地址已经被使用，那我们就可以寻找下一个位置，也就是索引为 1 的地址，发现还未被使用过，所以我们就可以把 Jack 的电话号码存放在这里。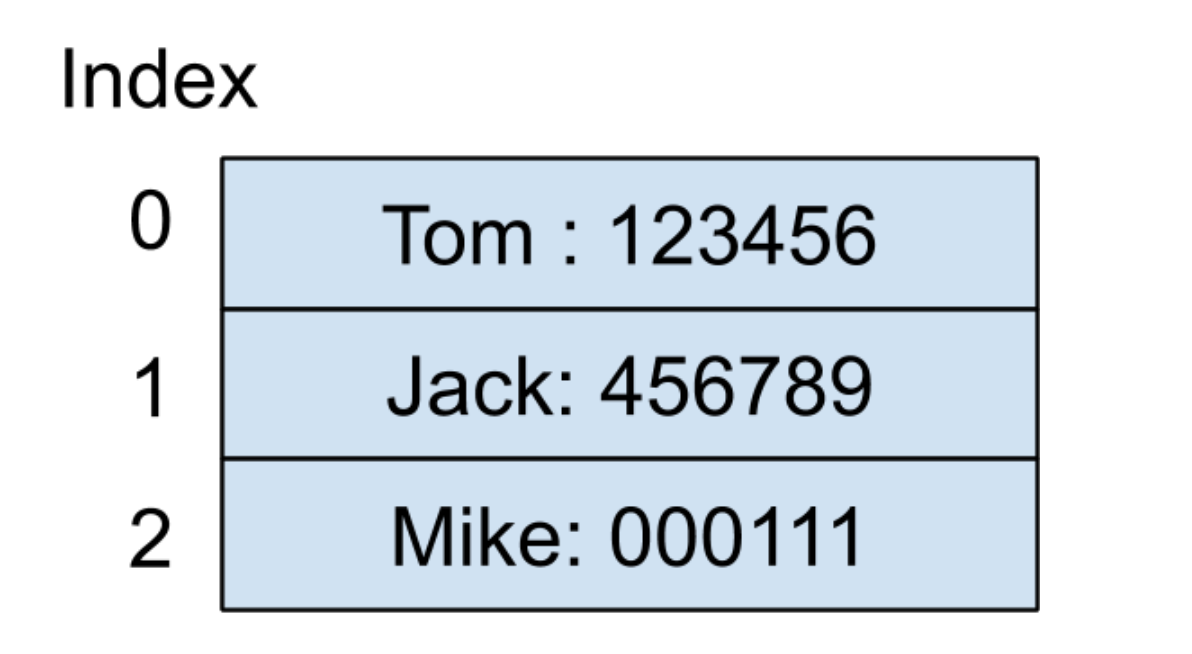因为在产生了哈希碰撞之后，我们无法确定数组里面保存的值到底是哪一个键产生的，所以必须将键也一并保存在数组中，内存结构如下图所示：  现在我们继续输入第三个键值对（Mike：000111）到哈希表中。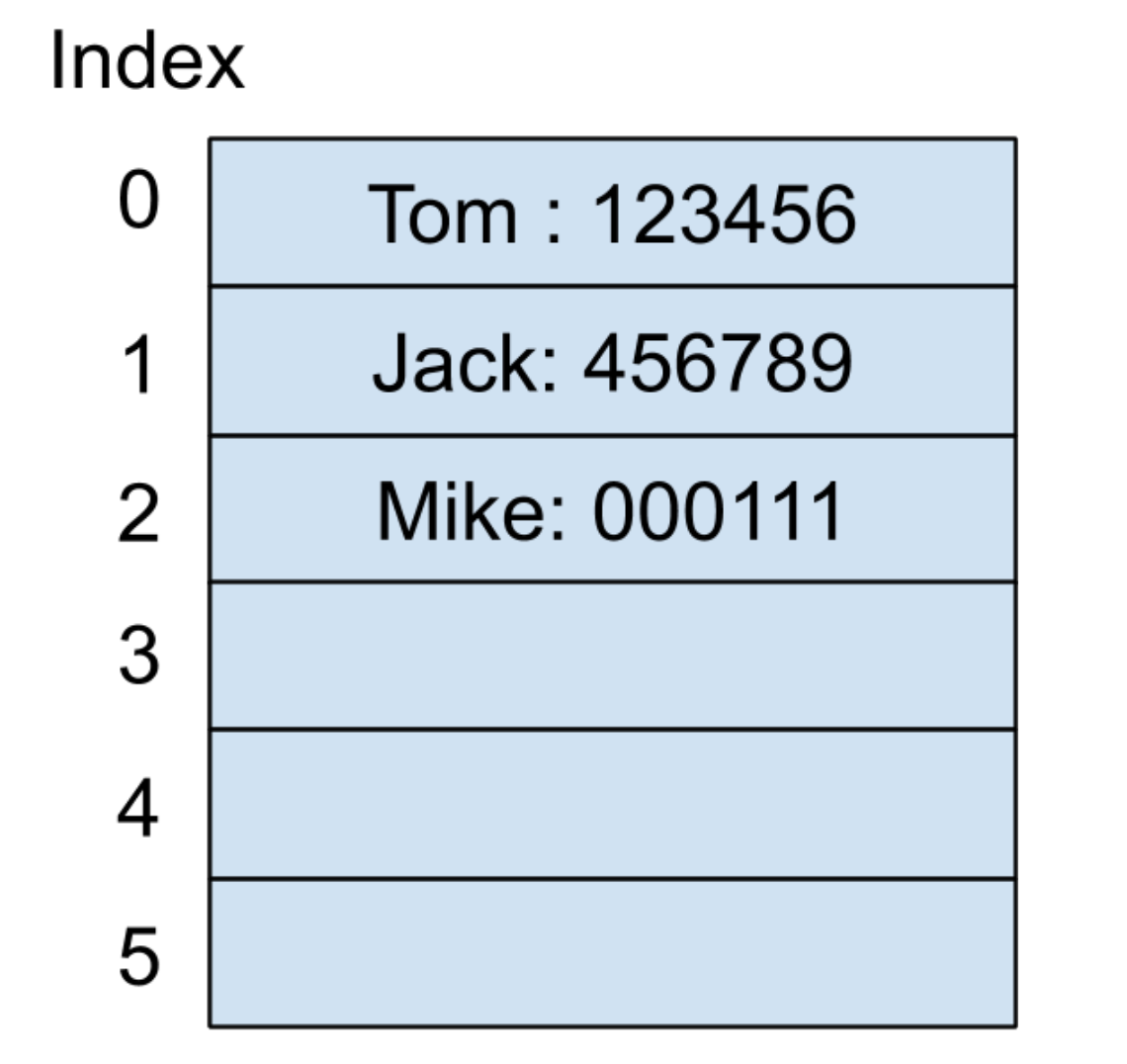假设 Mike 这个输入通过哈希函数产生的哈希值还是 0，按照线性探测的方法，先来看看下一个索引为 1 的地址，它已经被使用了，所以继续往下遍历到索引为 2 的地址，发现还未被使用，此时可以把 Mike 的电话号码存放在这里，内存结构如下图所示：  这时候你已经发现了，保存键值对的数组已经满了，如果再有新的元素插入的话，就无法保存新的键值对了。一般的做法是将这个数组扩容，比如，再创建一个新的数组，其大小为原来数组大小的两倍，然后把原来数组的内容复制过去，如果采用这种做法的话，这时的内存结构图如下所示：  当然了，一般哈希表并不会等到这个数组满了之后再进行扩容，其实底层数据结构会维护一个叫做负载因子（Load Factor）的数据，负载因子可以被定义为是哈希表中保存的元素个数 / 哈希表中底层数组的大小。当这个负载因子过大时，则表示哈希表底层数组所保存的元素已经很多了，所剩下的未被使用过的数组位置会很少，同时产生哈希碰撞的概率会很高，这并不是我们想看到的。所以一般来说，在负载因子的值超过一定值的时候，底层的数组就得需要进行扩容了，像在 Java 的 JDK 中，都会把负载因子的默认值设为 0.75 （源码地址）。 采用这种线性探测的好处是算法非常简单，但它也有自身的缺点。因为每次遇到哈希碰撞的时候都只是往下一个元素地址检测是否有未被使用的位置存在，所以有可能会导致一种叫做哈希聚集（Primary Clustering）的现象。我们来看看刚刚例子的内存结构图：  哈希表保存的元素现在都聚集在了 0、1、2 这三个索引位置的地方，如果有新的元素需要插入，而它的哈希值为 1 的话，本来这个位置是不应该产生哈希碰撞的，但由于采用了线性探测的方法，使得这个位置被占用了，所以新插入的元素还得重新再进行一次线性探测。 对此有一些改进的算法被提出用以缓解上面所说的哈希聚集问题，比如平方探测（Quadratic Probing）和二度哈希（Double Hashing）。 * 平方探测指的是每次检查空闲位置的步数为平方的倍数。例如说，当新元素插入的键所产生的哈希值为 i，那下一次的检测位置为：i 加上 1 的平方、i 减去 1 的平方、i 加上 2 的平方、i 减去 2 的平方、…，以此类推。 * 二度哈希指的是数据结构底层会保存多个哈希函数，当使用第一个哈希函数算出的哈希值产生了哈希碰撞之后，将会使用第二个哈希函数去运算哈希值，…，以此类推。 * [ ] 分离链接法（Separate Chaining） 分离链接法与链表有很大的关系，它的本质是将所有的同一哈希值的键值对都保存在一个链表中，而哈希表底层的数组元素就是保存这个哈希值对应的链表。 下面我们还是假设存储哈希表的底层数据结构是一个大小为 3 的数组，还是以保存好友电话号码为例，刚开始的内存结构图如下图所示：  同样假设第一个输入的键值对是（Tom：123456），表示好友的名字为 Tom，电话号码为 123456。同时假设 Tom 这个字符串在通过哈希函数之后所产生的哈希值是 0，因为 0 这个索引位置并未使用，所以我们创建一个新的链表节点，将键值对的值保存在这个新节点中，而 0 这个索引位置的值就是指向新节点的地址，内存结构如下图所示：  紧接着，我们输入第二个键值对（Jack：456789），同时假设 Jack 这个字符串在通过哈希函数之后所产生的哈希值也是 0，而因为索引为 0 的位置已经存放一个值了，也就表示这时候产生了哈希碰撞。但是没关系，我们只需要再创建一个新的链表节点，将这个键值对的值保存在新节点中，然后将这新节点插入索引 0 位置链表的结尾，内存结构如下图所示：  采用分离链接法会使用到额外的空间来保存新插入的键值对。虽然这里举的例子采用的是链表，这在查找一个键对应的值时，有可能时间复杂度会降级为 O(N)，但很多时候我们可以进一步将存储结构优化成红黑树，这在树的章节将会讲解到，在 Java JDK 中的 HashMap 类其实就是使用了分离链接法。 * [ ] Bloom Filter Bloom Filter 是一个哈希表和位数组相结合的基于概率的数据结构，由 Bloom 在 1970 年提出。它主要用于在超大的数据集合中判断一个元素是否存在这个集合中，像判断一个人是否在黑名单中一样，或者判断一封邮件是否属于垃圾邮件的范畴等等。因为使用了位数组，所以使得 Bloom Filter 在空间利用率上非常的高效。而同时它的底层原理和哈希表一致，使得它在查找的时间复杂度上也十分优秀。为什么说它是基于概率的数据结构呢？下面来看看它的原理你就明白了。 Bloom Filter 的原理是将一个元素通过多个哈希函数映射到位数组中。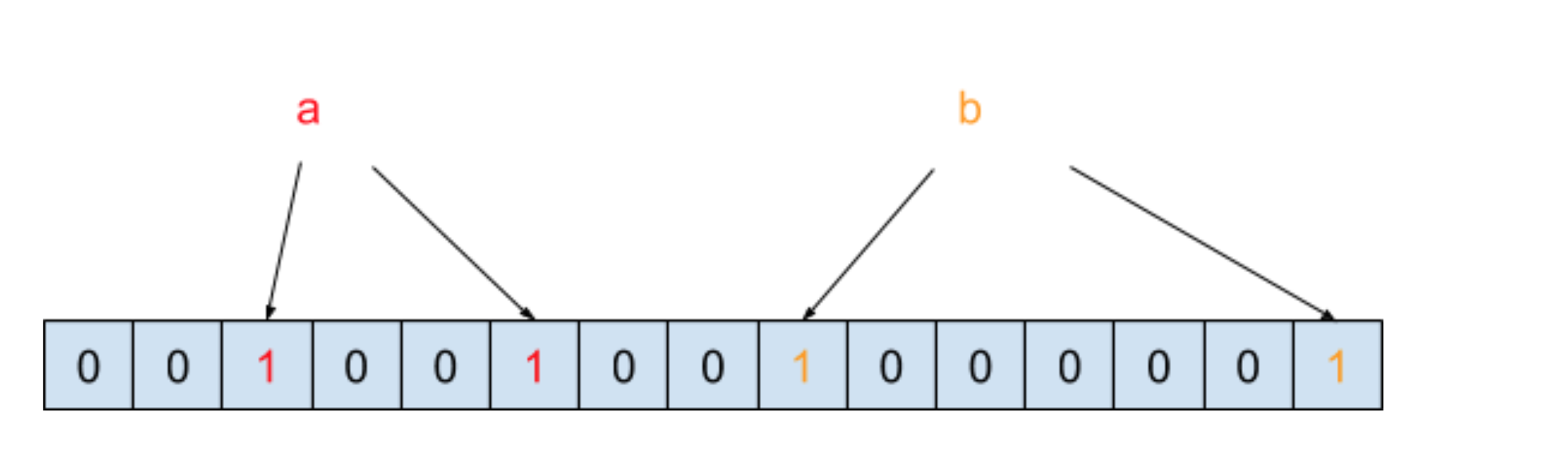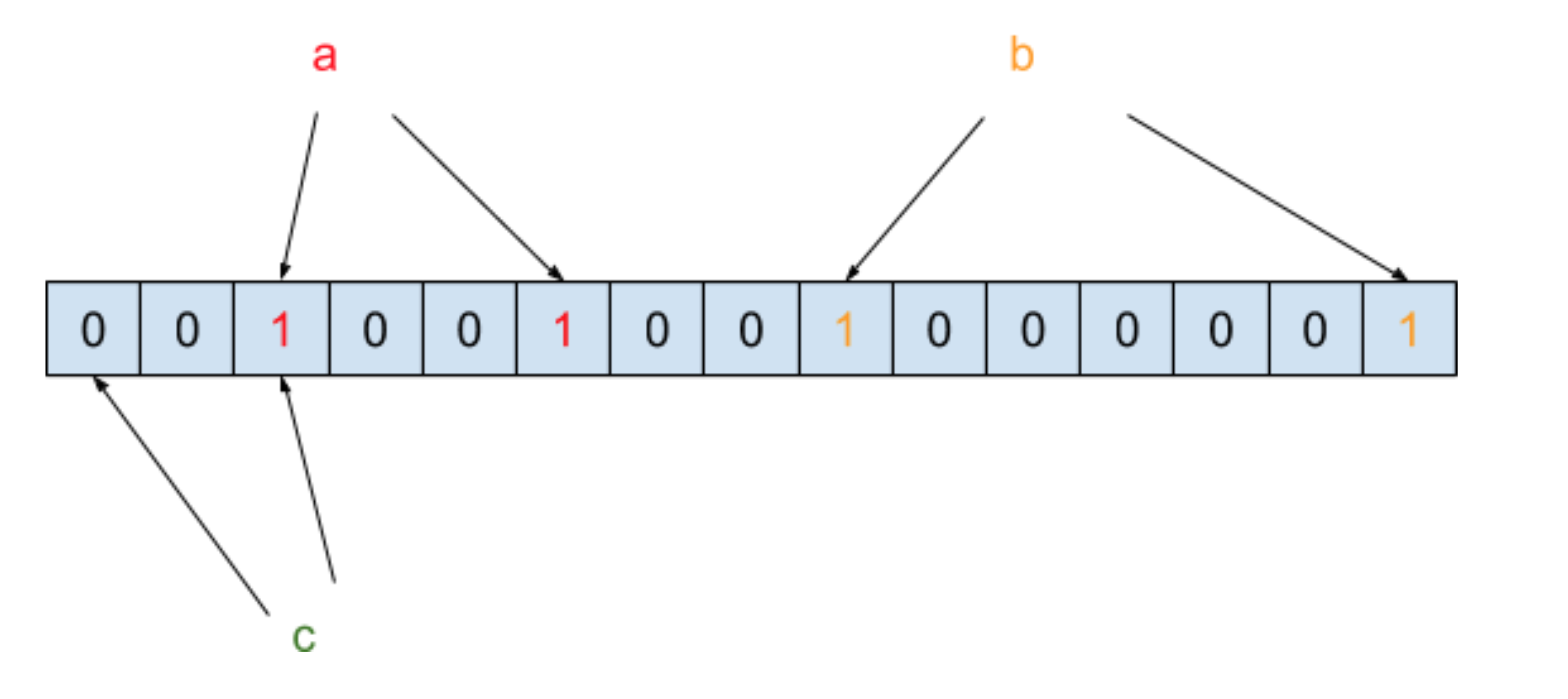我们以黑名单为例来说明，假设哈希函数的个数为 2，也假设黑名单中只有 a 和 b 两个元素，在通过两次哈希函数映射到位数组之后，内存结构图如下图所示：  我们把元素经过两次哈希函数之后所对应的哈希值的位置设为 1，此时需要判断元素 c 是否在黑名单中，需要将 c 也进行两次哈希函数运算，得到的结果如下图所示：  你会发现 c 在经过哈希函数映射之后有一个哈希值对应的位置结果为 0，那就表示 c 这个元素一定不在黑名单中。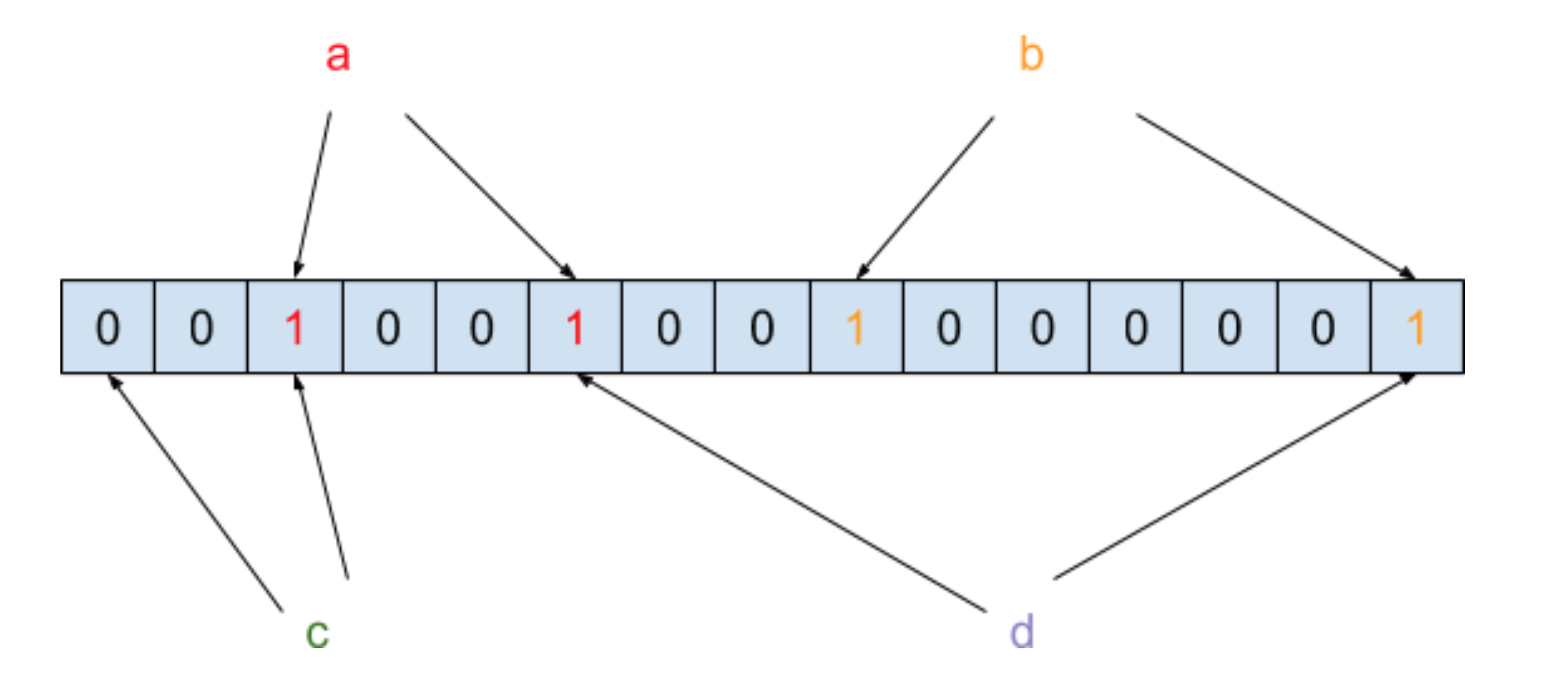此时我们再来还需要判断元素 d 是否在黑名单中，需要将 d 也进行两次哈希函数运算，得到的结果如下图所示：  你会发现 d 在经过哈希函数映射之后有两个哈希值所对应的位置结果都为 1，但是我们只能判断 d 这个元素有可能在黑名单中。所以这里存在一个误判率，也就是说即便经过 N 个哈希函数之后哈希值对应位置的结果都为 1 了，但这个元素不一定真的存在集合中。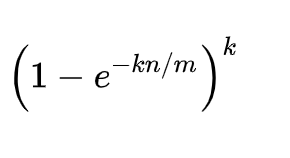 误判率的公式如下：  其中，m 表示位数组里位的个数，n 表示已经存储在集合里的元素个数，k 表示哈希函数的个数。