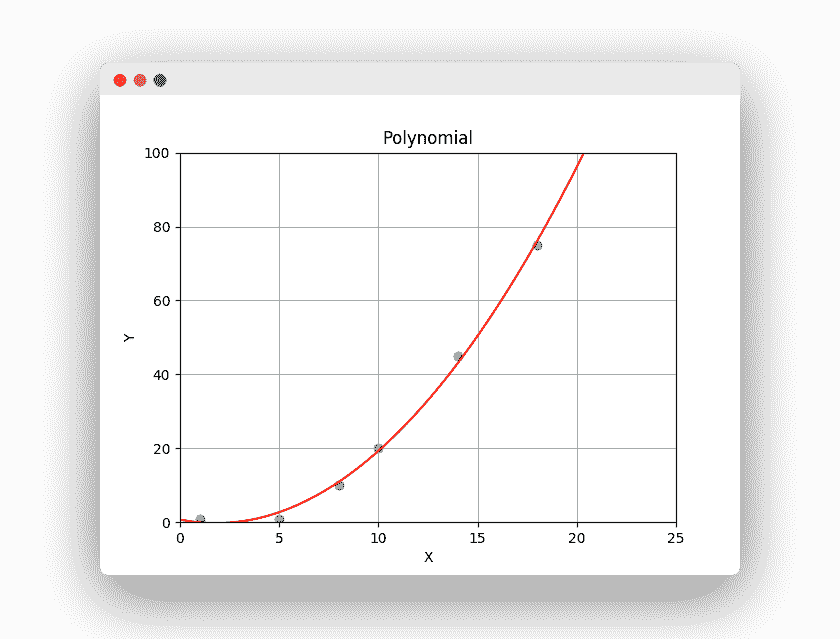
# Python 中的多项式回归 > 原文： [https://pythonbasics.org/polynomial-regression-in-python/](https://pythonbasics.org/polynomial-regression-in-python/) 多项式回归可能非常有用。 X 和 Y 之间并不总是存在线性关系。有时，该关系是指数级或 N 阶。 ## 回归 ### 多项式回归 您可以绘制 X 和 Y 之间的多项式关系。如果没有线性关系，则可能需要多项式。 与线性关系不同，多项式可以更好地拟合数据。  您只需一行代码即可创建此多项式行。 ```py poly_fit = np.poly1d(np.polyfit(X,Y, 2)) ``` 那将训练算法并使用二阶多项式。 训练后，您可以使用一个新示例通过调用`polyfit`来预测值。 然后它将输出一个连续值。 ### 示例 下面的示例在收集到的数据上方绘制了一条多项式线。 它训练算法，然后预测连续值。 ```py import numpy as np import matplotlib.pyplot as plt X = [1, 5, 8, 10, 14, 18] Y = [1, 1, 10, 20, 45, 75] # Train Algorithm (Polynomial) degree = 2 poly_fit = np.poly1d(np.polyfit(X,Y, degree)) # Plot data xx = np.linspace(0, 26, 100) plt.plot(xx, poly_fit(xx), c='r',linestyle='-') plt.title('Polynomial') plt.xlabel('X') plt.ylabel('Y') plt.axis([0, 25, 0, 100]) plt.grid(True) plt.scatter(X, Y) plt.show() # Predict price print( poly_fit(12) ) ``` ### 过拟合和欠拟合 切勿过拟合或欠拟合，这是很重要的，您想抓住这种关系但又不能完全遵循这些要点。 线性关系会欠拟合，而过拟合会选择程度高到可以拟合点的程度。 相反，您想要捕获关系。 [下载示例和练习](https://gum.co/MnRYU)