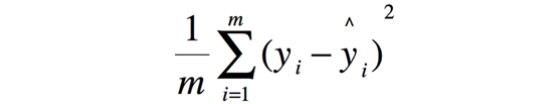
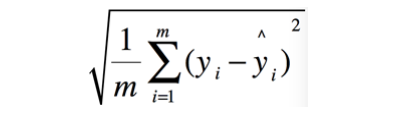
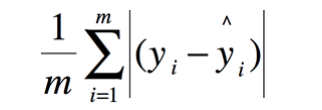
[TOC] ## 1.概念 * 回归分析(Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。 * 回归与分类的区别：回归预测的是连续变量（数值），分类预测的是离散变量（类别）。 2.回归的评估 * 均方误差（Mean Squared Error, MSE）  注意：在使用cross\_val\_score计算时，MSE的分数用“neg\_mean\_squared\_error”计算一个负值，类为score代表的是分数，越高越好，显然MSE是越低越好，它是一种loss，越低越好。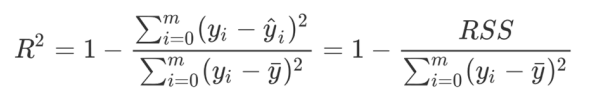 * 均方根误差（Root Mean Squared Error, MSE）  * 平均绝对误差（Mean Absolute Error, MAE）  * 中值绝对误差（Median Absolute Error） * 决定系数（Coefficient of Determination，R2）  * sklearn的metrics模块中提供了如下回归的相关指标： • max_error •mean_absolute_error •mean_squared_error •mean_squared_log_error •median_absolute_error •mean_tweedie_deviance •mean_poisson_deviance •mean_gamma_deviance •r2_score •explained_variance_score **3）线性回归** 线性回归(Linear Regression)：因变量（Y）和一个或多个自变量（X）之间建立一种线性方程关系 * linear_model.LinearRegression * 重要属性：coef_和intercept_ * 求解方法：最小二乘法 * 问题—多重线性关系： * “精确相关关系”（完全相关）：行列式为0 * “高度相关关系”：行列式不为0，但是一个非常接近0的数 **4）Ridge（岭回归）** 岭回归,又称为吉洪诺夫正则化（Tikhonov regularization）,在多元线性回归的损失函数上加上了正则项，表达为系数ω的L2范式（即系数ω的平方项）乘以正则化系数。 * linear_model.Ridge **5）Lasso回归** Lasso回归，Lasso全称最小绝对收缩和选择算子（least absolute shrinkage and selection operator），使用的是系数ω的L1范式（L1范式则是系数ω的绝对值）乘以正则化系数 。 * linear_model.Lasso **6）弹性网(Elastic Net)** 弹性网(Elastic Net)，是一种使用L1,L2范式作为先验正则项训练的线性回归模型。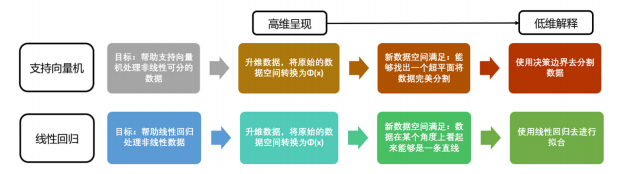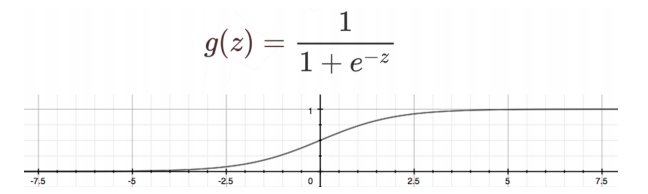 **7）多项式回归**  对线性回归问题，如果数据不是线性关系，采用**多项式变换**的方式对特征数据进行升维 * preprocessing.PolynomialFeatures **8)逻辑回归**  * linear_model.LogisticRegression