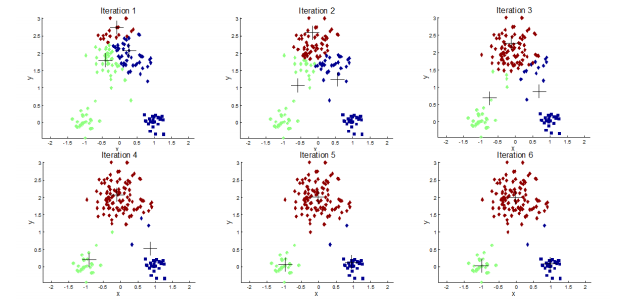
[TOC] ## **1.概念** 聚类（Clustering）分析是依据物以类聚的原理，将没有类别的对象根据对象的特征自动聚集成不同簇的过程，使得属于同一个簇的对象之间要尽可能非常相似，属于不同簇的对象之间要尽可能不相似(簇内相似度高，簇间相似度低)。 聚类算法需要注意的地方: * 距离/相似度的度量 * 数据的标准化  ## **2.聚类的评估** * 簇内平方和（Inertia） * 属性Inertia_ * 轮廓系数 * silhouette_score * silhouette_score * 卡林斯基-哈拉巴斯指数 * calinski_harabasz_score ## **3.基于划分的聚类** ### **1）K-means算法步骤**  ### **2）K-means缺点** * 需要预先设定K值，对最先的K个点选取很敏感 * 对噪声和离群值非常敏感 * 只适合对数值型数据聚类 * 不能解决非凸（non-convex）数据 ### **3) K-means改进** * k-means对初始值的设置很敏感，所以有了k-means++、intelligent k-means、genetic kmeans。 * k-means对噪声和离群值非常敏感，所以有了k-medoids和k-medians。 * k-means只用于numerical类型数据，不适用于categorical类型数据，所以k-modes。 * k-means不能解决非凸（non-convex）数据，所以有了kernel k-means。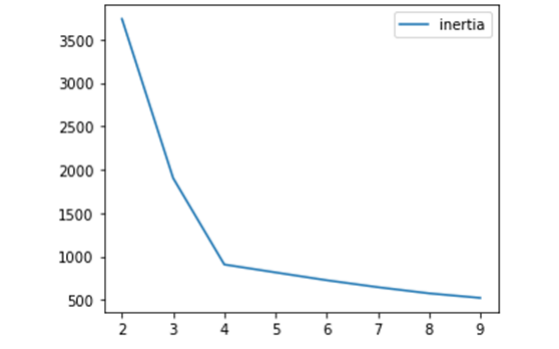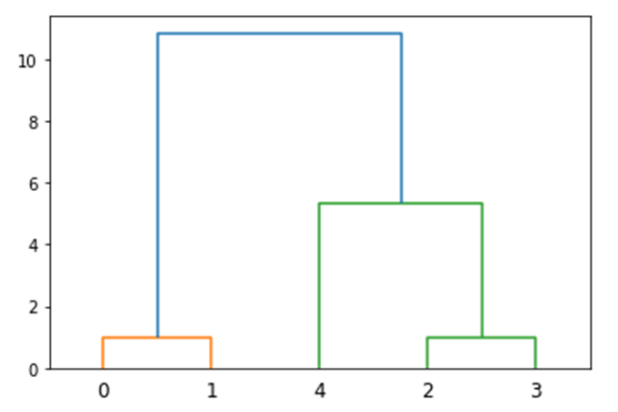 * K值的选择：**肘点法**  ## **4.基于层次的聚类**  层次聚类（hierarchical clustering）方法将数据对象组成一棵聚类树 * 分裂法 * 凝聚法 ### **1）凝聚法的步骤** 1. 计算各数据间的相似度矩阵 2. 每个数据就是一个簇 3. Repeat。 4. 合并两个最相似的簇形成新簇 5. 更新相似度矩阵 6. 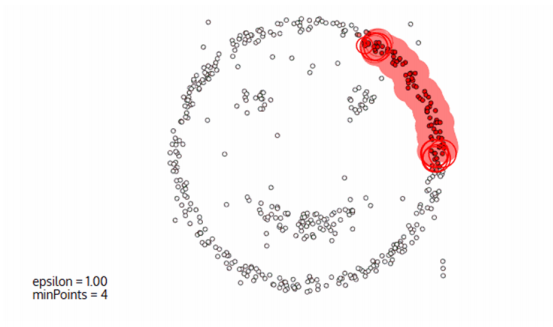Until只剩一个类簇 ### **2）簇间相似度的度量** * MIN(单连接) * MAX(全连接) * Group Average(组平均) * Distance Between Centroids(质心距离) ### **3）cluster.AgglomerativeClustering** ## **5.基于密度聚类**  **DBSCAN**（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，它将簇定义为密度相连的点的最大集合。 ### **1）概念** * ϵ-领域：点x的ϵ-领域是以该对象为中心，ϵ为半径的空间,ϵ-领域可以写成NEps(x)：NEps(x) : {y belongs to D | dist(y,x) <= Eps} * 密度：特定半径内(Eps)数据点的数量 * 核心点（Core Point）： 用户指定一个参数MinPts,即指定稠密区域的密度阈值。如果一个点的ϵ-领域至少包含MinPts个点，则称该点为核心点 * 边界点(Border point)：对于点p，如果它的ϵ-领域内包含的点少于MinPts个，但落在某个核心点的ϵ-领域内，则称点p为边界点 * 噪声点（Noise）：既不是核心点又不是边界点的任何点 ### **2）优点** * 发现任意形状的聚类 * 处理噪音 ### **3）缺点** * 参数难以确定 * 效果不佳： * 密度不均 * 高维数据 ### **4）cluster.DBSCAN**