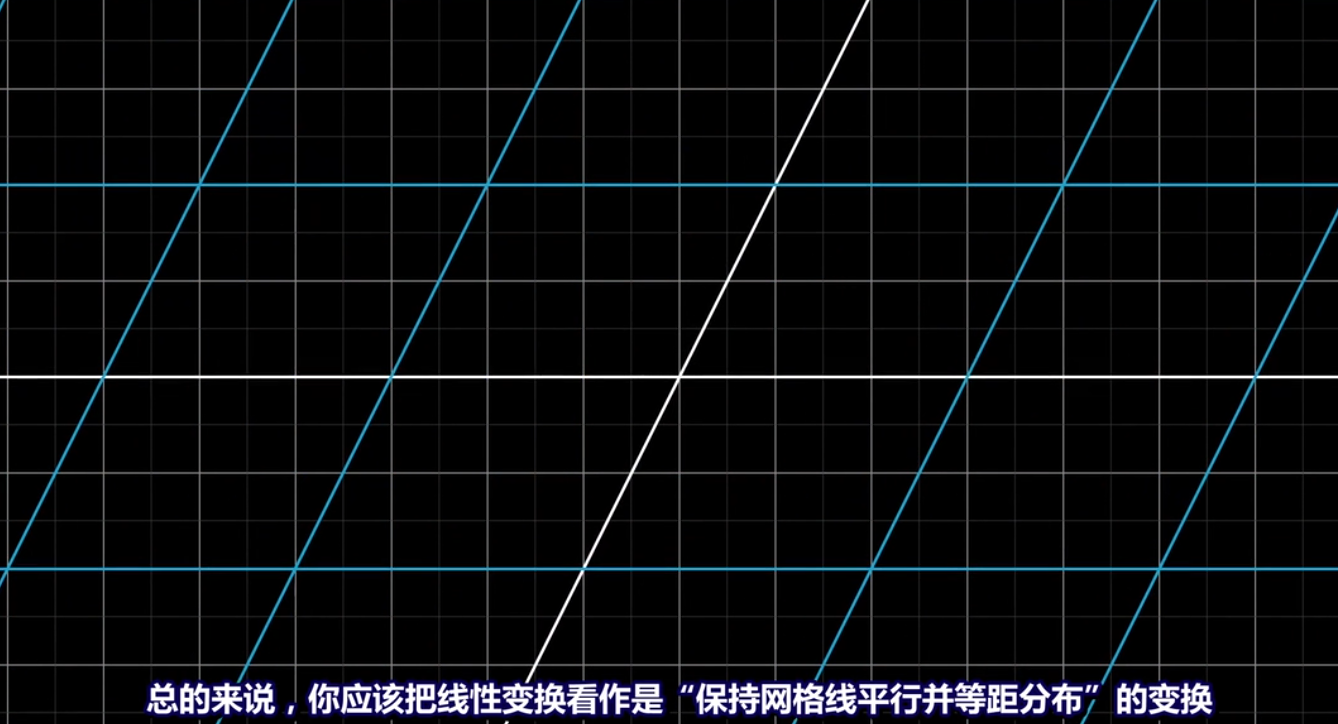
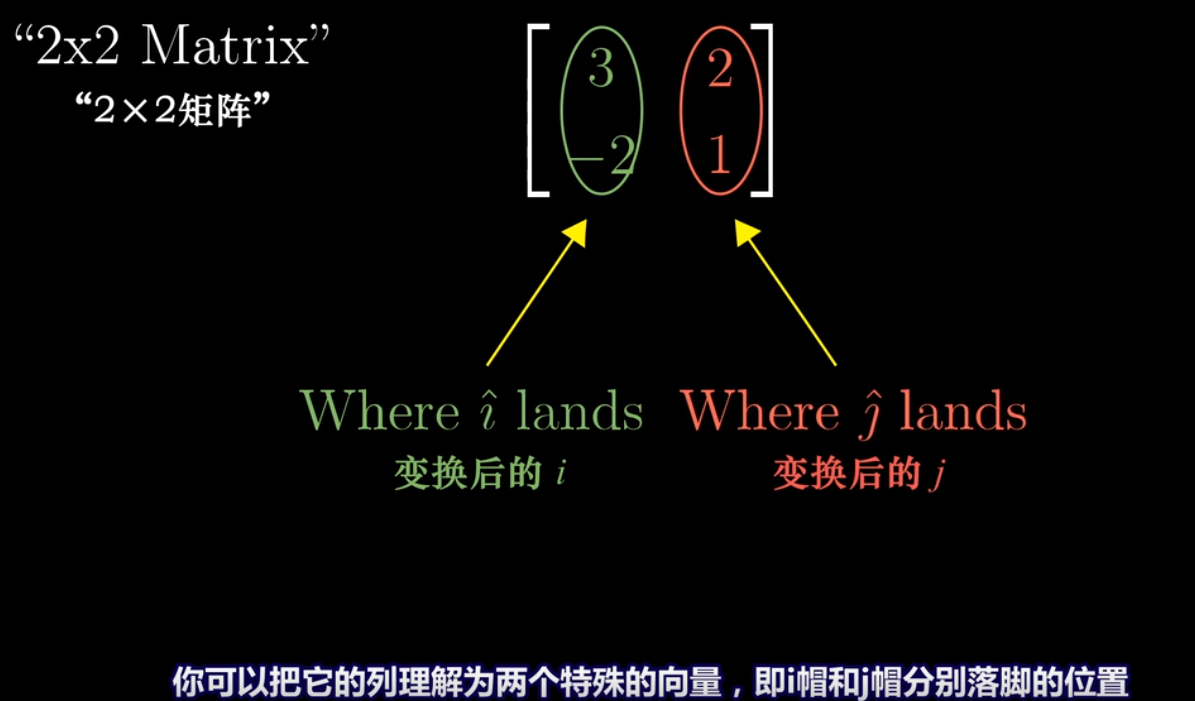
线性变换是函数的一种说法。 在原坐标系中，任一向量都可以通过基向量的某种线性组合来得到。 **变换**暗示以特定方式可视觉化这一输入-输出关系。 **线性变换特点**：1.一条直线变换后仍为直线 2.原点保持固定 **线性变换解释**:先对基向量i的坐标进行移动，使 i 向量所在直线和其他平形直线同时进行旋转和缩放。i 向量所在直线原点不变。再对基向量j的坐标进行移动，使 j 向量所在直线和其他平形直线同时进行旋转和缩放。j 向量所在直线原点不变。  ***** **对原坐标系中向量的理解** i 向量坐标[ 1 0] j向量坐标[0 1] ,在原坐标系中。[3 -5]既是一个向量，也可以看作 3i + (-5j)这个特定线性组合中的标量数字序列 ***** **用数值描述线性变换 2*2矩阵和1*2矩阵相乘的几何意义** 一个线性变换可以通过记录两个基向量 i 和 j 变换后坐标来描述这种变换。2*2矩阵表示二维坐标的变换信息  ***** 对于原坐标系中一个给定向量，是基向量的特定线性组合v = ai +b j。对坐标系变换后，求变换后向量的坐标，v(变换后)= a*(变换后的i) + b* (变换后的j)  用数学公式表达如下图： 下图式子的含义，（经过变换后的基向量i j）* (线性组合的标量数字序列) = 得到（变换后的基向量通过线性组合生成的新向量。新向量用2*2矩阵表示，左边是x*(变换后的i),右边是y*（变换后的j）  *****