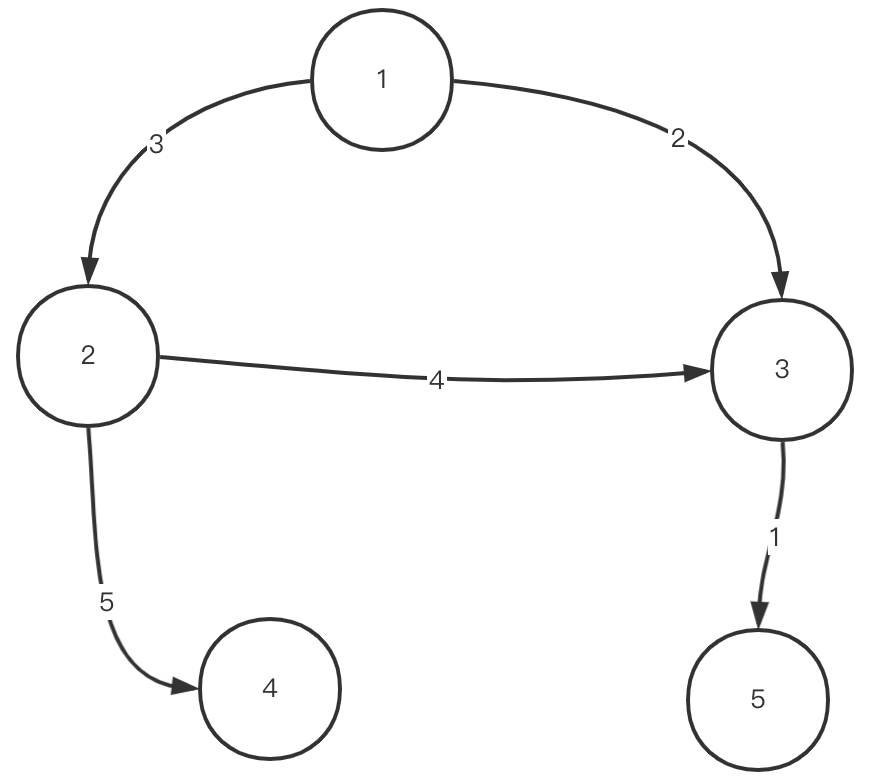
## 图的表达方式及创建 ### 二维数组表示法  ~~~ int[][] data = { {1,2,3}, // 顶点1到顶点2有一条权值为3的边 {2,3,4},// 顶点2到顶点3有一条权值为4的边 {1,3,2}, {2,4,5}, {3,5,1} }; ~~~ ### 按数据创建无向图 ~~~ Graph graph = Graph.createGraphUnDirect(data); ~~~ ~~~ /** * 从数组场景创建无向图 * @param data eg,{{1,3,2},{2,3,3}} * 表示 从顶点1到顶点3有权值为2的边；顶点3到顶点1权值为2的边 * 从顶点2到顶点3有权值为3的边；顶点3到顶点2权值为3的边 * @return */ public static Graph createGraphUnDirect(int[][] data){ Graph graph = new Graph(); for(int i=0;i<data.length;i++){ String from = data[i][0] + ""; String to = data[i][1] + ""; Integer weight = data[i][2]; // 将from顶点和to顶点加入到图里 if(!graph.vertexs.containsKey(from)){ graph.vertexs.put(from,new Vertex(from)); } if(!graph.vertexs.containsKey(to)){ graph.vertexs.put(to,new Vertex(to)); } // 从图里获取from和to顶点 Vertex fromVertex = graph.vertexs.get(from); Vertex toVertex = graph.vertexs.get(to); // 创建从from顶点到to顶点的边 Edge edge = new Edge(weight,fromVertex,toVertex); // 创建反向的边 Edge reverseEdge = new Edge(weight,toVertex,fromVertex); // from和to顶点的入度和出度都+1 fromVertex.out++; fromVertex.in++; toVertex.out++; toVertex.in++; // 将to顶点加入到from顶点里的点集nexts里 fromVertex.nexts.add(toVertex); // 将from顶点加入到to顶点里的点集nexts里 toVertex.nexts.add(fromVertex); // 将边加入到from顶点的边集里 fromVertex.edges.add(edge); // 将反向边加入到to顶点的边集里 toVertex.edges.add(reverseEdge); // 将边加入到图里 graph.edges.add(edge); // 将反向边加入到图里 graph.edges.add(reverseEdge); } return graph; } ~~~ ### 按数组创建有向图 ~~~ Graph graph = Graph.createGraph(data); ~~~ ~~~ /** * 从数组场景创建有向图 * @param data eg,{{1,3,2},{2,3,3}} * 表示 从顶点1到顶点3有权值为2的边； * 从顶点2到顶点3有权值为3的边 * @return */ public static Graph createGraph(int[][] data){ Graph graph = new Graph(); for(int i=0;i<data.length;i++){ String from = data[i][0] + ""; String to = data[i][1] + ""; Integer weight = data[i][2]; // 将from顶点和to顶点加入到图里 if(!graph.vertexs.containsKey(from)){ graph.vertexs.put(from,new Vertex(from)); } if(!graph.vertexs.containsKey(to)){ graph.vertexs.put(to,new Vertex(to)); } // 从图里获取from和to顶点 Vertex fromVertex = graph.vertexs.get(from); Vertex toVertex = graph.vertexs.get(to); // 创建从from顶点到to顶点的边 Edge edge = new Edge(weight,fromVertex,toVertex); // from顶点的出度+1，to顶点的入度+1 fromVertex.out++; toVertex.in++; // 将to顶点加入到from顶点里的nexts里 fromVertex.nexts.add(toVertex); // 将边加入到from顶点的边集里 fromVertex.edges.add(edge); // 将边加入到图里 graph.edges.add(edge); } return graph; } ~~~ ### 字符箭头数组表示法  ~~~ 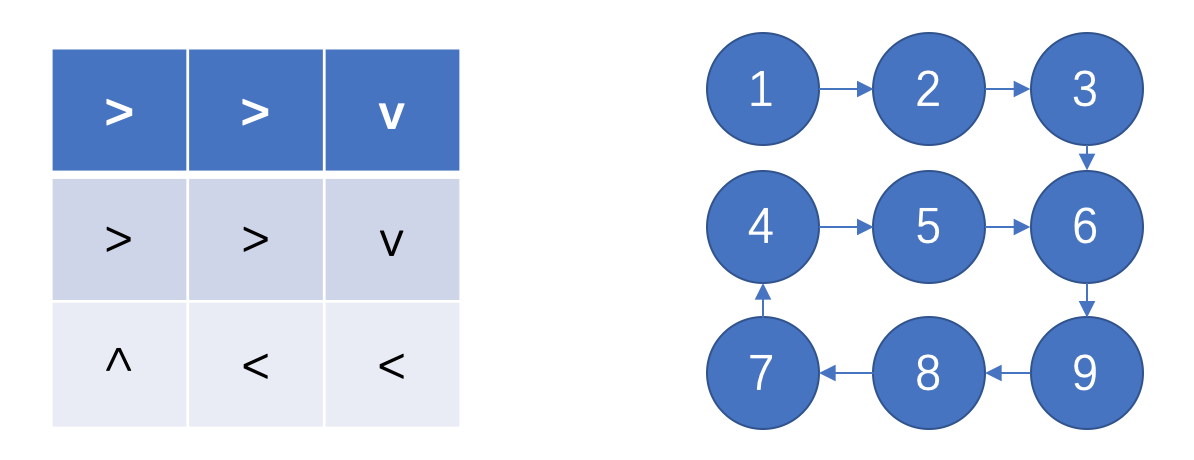String[] arrows = {">>v",">>v","^<<"}; ~~~ ~~~ /** * 从箭头数组场景创建有向图 * @param arrows eg, 自主编号 * { * ">>v", 1,2,3 * "v^<", 4,5,6 * "<><" 7,8,9 * } * 表示 从顶点1到顶点2有边；顶点2到顶点3有边；顶点3到顶点6有边 * 顶点4到顶点7有边；顶点5到顶点2有边；顶点6到顶点5有边 * 顶点8到顶点9有边；顶点9到顶点8有边 * @return */ public static Graph createGraphFromArrowString(String[] arrows){ Graph graph = new Graph(); int row = arrows.length; int col = arrows[0].length(); // 设置上下左右的坐标规则 Map<Character,int[]> ruleMap = new HashMap<>(); ruleMap.put('^',new int[]{-1,0}); ruleMap.put('v',new int[]{1,0}); ruleMap.put('<',new int[]{0,-1}); ruleMap.put('>',new int[]{0,1}); for(int i=0;i<row;i++){ for(int j=0;j<col;j++){ String from = (i * col + j + 1) + ""; int[] rule = ruleMap.get(arrows[i].charAt(j)); int nextI = i + rule[0]; int nextJ = j + rule[1]; String to = (nextI * col + (nextJ + 1)) + ""; // 无权，默认为1 Integer weight = 1; // 判断to点的坐标在合法范围内 if(nextI >=0 && nextI < row && nextJ >=0 && nextJ < col){ // 将from顶点和to顶点加入到图里 if(!graph.vertexs.containsKey(from)){ graph.vertexs.put(from,new Vertex(from)); } if(!graph.vertexs.containsKey(to)){ graph.vertexs.put(to,new Vertex(to)); } // 从图里获取from和to顶点 Vertex fromVertex = graph.vertexs.get(from); Vertex toVertex = graph.vertexs.get(to); // 创建从from顶点到to顶点的边 Edge edge = new Edge(weight,fromVertex,toVertex); fromVertex.out++; toVertex.in++; // 将to顶点加入到from顶点里的点集nexts里 fromVertex.nexts.add(toVertex); // 将边加入到from顶点的边集里 fromVertex.edges.add(edge); // 将边加入到图里 graph.edges.add(edge); } } } return graph; } ~~~