# 19.1 计划 > 原文： [http://math.mit.edu/~djk/calculus_beginners/chapter19/section01.html](http://math.mit.edu/~djk/calculus_beginners/chapter19/section01.html) 这种材料不是微分方程课程的替代品，这些课程倾向于提供洞察力和方法，允许对许多重要的微分方程进行代数求解，并提供对无需解决的解决方案行为的深入了解详细地。 我们在这里提供它是因为微分方程中的许多传统课程完全忽略了数值计算，我们希望表明，对于各种微分方程，这些可以通过大量工作完成，而不是超出数值积分所涉及的范围。 我们将首先解决一阶微分方程，然后考虑一个二阶方程，最后一个描述行星运动，它是二阶的并且有两个因变量。 （虽然行星在三维空间中移动，但它们的运动位于一个平面上。我们的因变量则是行星的和坐标，自变量是时间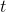。） 它们之间的主要区别在于需要创建的列数。 **“我们”是什么意思。我睡觉的时候你会这样做吗？** 好吧，我会告诉你如何设置一个，你会看到你可以不费吹灰之力地改变方程式并自己解决它们，这给你前几代学生所不知道的力量。