# Java 广度优先搜索示例 > 原文： [https://javatutorial.net/breadth-first-search-example-java](https://javatutorial.net/breadth-first-search-example-java) 当涉及从给定数据结构访问数据时，搜索或遍历非常重要。 在这些数据结构中，例如[图](https://javatutorial.net/graphs-java-example)和树，有多种遍历/搜索元素的方法。  广度优先搜索是这些方法的一个示例。 BFS 是一种遍历树或图形的算法，它从树的根（树中的最高节点）开始或仅从顶部开始，并在当前深度扫描所有相邻节点，然后再继续移动到节点或元素。 下一个深度级别。 简而言之，BFS 必须完成一层，然后继续进行下一层直到没有剩余的任何层。 BFS 使用与深度优先搜索完全相反的工作流程，反之亦然。 在 BFS 和 DFS 之间的实现方面，一个很大的不同是 BFS 使用队列，而 DFS 使用栈。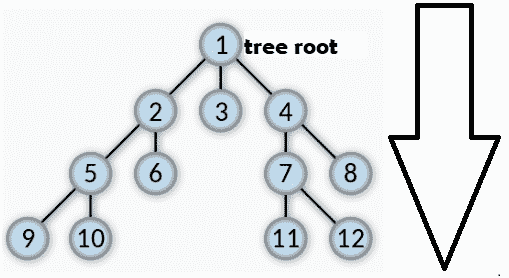  BFS 的工作流程 ## BFS 的实现 实现 BFS 时要遵循两个简单的规则： 1. 访问给定层上的每个元素 2. 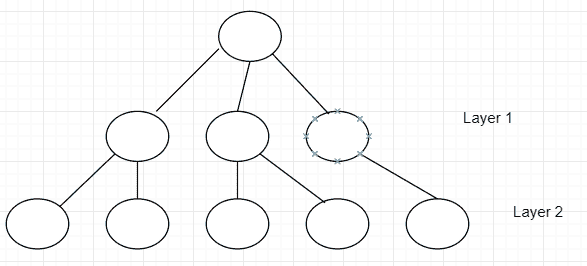移至下一层 一个例子：  在继续进行第 2 层之前，必须先通过第 1 层。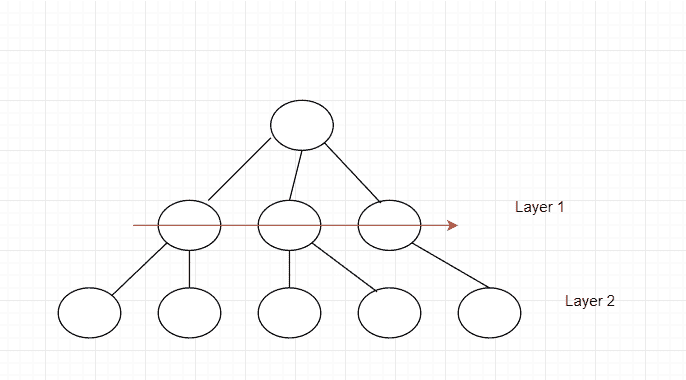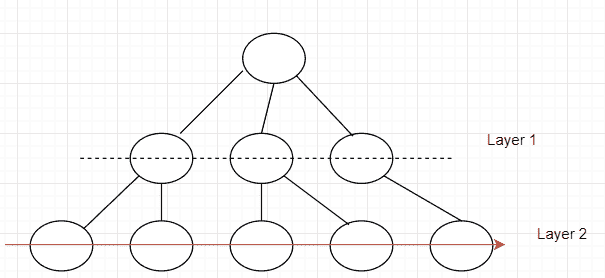  在那之后，这是应该怎么做的：  **伪代码** ```java public void breadthFirstSearch(Graph G, Object S) // G => Graph ; S => Source node { define a queue named as Queue; insert the source node in the Q mark s as visited perform a while loop that keeps looping until the queue is not empty removing the current element from the queue as it will be visited now perform a for loop that goes through all neighbours of the current element if condition that checks if the current element/node/vertex is not visited if it has not been visited, enqueue it and mark it as visited } ``` **实际代码实现** ```java public void BFS(int s, int l) { // create an array that holds boolean values that will have length 'l' boolean visited[] = new boolean[l]; // create a queue LinkedList<Integer> q = new LinkedList<Integer>(); // mark the current node as visited and add it to the queue visited[s]=true; q.add(s); while (q.size() != 0) { // dequeuing a vertex from queue s = q.poll(); // get all adjacent vertices of the dequeued vertex if a adjacent has not // been visited, then mark it visited and enqueue it Iterator<Integer> k = adj[s].listIterator(); while (k.hasNext()) { int j = k.next(); if (!visited[j]) { visited[j] = true; q.add(j); } } } } ```