向量运算法则在后面的算法推倒中会用到。

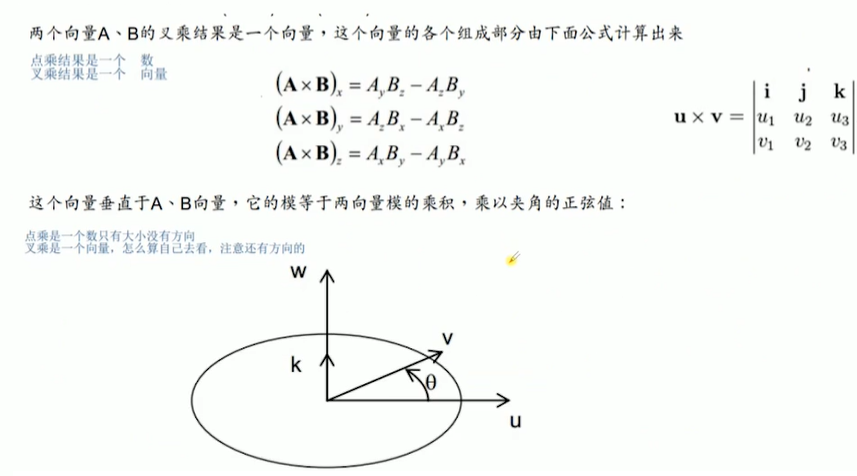
飞控中使用的姿态表示法有:欧拉角、旋转矩阵、四元数。
[TOC]
# 1. 坐标系
姿态用来描述地球坐标系与机体坐标系之间的角关系,其姿态解算需要解决的是如何表示四旋翼与地球坐标系的相对姿态。所以在这里分别建立地球坐标系与机体坐标系,才能更清楚地描述它们之间的关系,如图4-3。

定义两个坐标系Z轴(上图未画出)的正方向为重力加速度g的方向,地球坐标系的原点为四旋翼起飞的地点,机体坐标系的原点为四旋翼重心位置。到这里坐标系就建立完成了。
# 2. 欧拉角
欧拉角的定义不仅仅和旋转角度有关系,还和旋转轴的旋转顺序有关系,任何一种旋转顺序都是合法的。根据定义,欧拉角有12种旋转顺序(维基),一个物体通过任意一个旋转顺序都可以达到同样的姿态,在各个学科里所以为了统一,航空航天领域规定XYZ为欧拉角的旋转顺序。
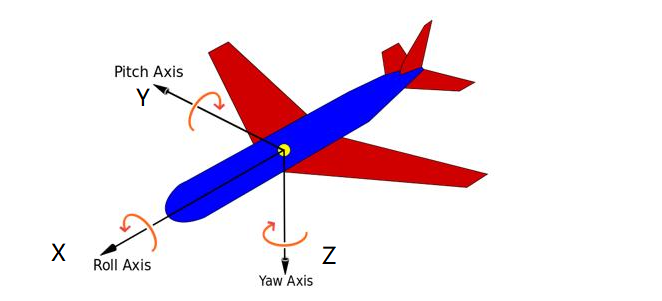
飞行器依次绕过不同的坐标轴连续转动三次,即可实现从一个坐标系转换到另一个坐标系,这三次转动的角度为绕X轴旋转得到的横滚角Roll、绕Y轴旋转得到的俯仰角Pitch,绕Z轴旋转得到的偏航角Yaw,这三个角就是欧拉角。
# 3. 旋转矩阵
在二维平面上,旋转矩阵定义如下,它可以将`$ O^{'} $`的坐标用`$ O $`坐标来表示,从而实现坐标系的转换。

从二维空间扩展到三维空间,就是让二维旋转矩阵分别绕 Z轴、Y轴、X轴(顺序不能调换)进行旋转,得到三个矩阵,将这三个矩阵相乘得到最终的旋转矩阵。

旋转矩阵简化后的表达式如下:

# 4. 四元数
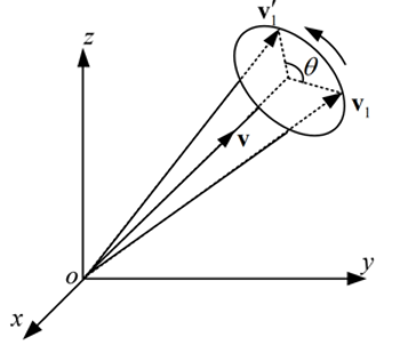
四元数姿态表达式是一个四个参数的表达式。它的基本思想是:一个坐标系到另外一个坐标系的变换可以通过绕一个定义在参考系中的矢量`$ \overrightarrow{u} $`一次性转动来实现。如下图所示,将`$ \nu^{'}_{1} $`向量用`$ \nu_{1} $`向量进行表示,可以按式(4-1)来转换:
:-: 
```[tex]
\begin{bmatrix}
0\\
\nu^{'}_{1}
\end{bmatrix} = \overrightarrow{q} \bigotimes \begin{bmatrix}
0\\
\nu_{1}
\end{bmatrix} \bigotimes \overrightarrow{q}^{-1}..................................................(4-1)
```
其中`$ \overrightarrow{q} = \begin{bmatrix}
cos\frac{\theta}{2} \\
\nu sin\frac{\theta}{2} \end{bmatrix} $`就是四元素。
四元素用矢量`$ \overrightarrow{q} $`来表示,四元数的表达方式共有5种,分别如下:
**(1)矢量式**
```[tex]
\overrightarrow{q}=q_{0}+\overrightarrow{q}_{u}..................................................(4-2)
```
`$ q_{0} $`为标量,`$ \overrightarrow{q}_{u} $`是三维空间的一个矢量。
**(2)复数式**
```[tex]
\overrightarrow{q}=q_{0}+q_{1}\overrightarrow{i}+q_{2}\overrightarrow{j}+q_{3}\overrightarrow{k}..................................................(4-3)
```
可视为一个超复数,`$ \overrightarrow{Q} $`的共轭复数记为:
```[tex]
\overrightarrow{q}^{'}=q_{0}-q_{1}\overrightarrow{i}-q_{2}\overrightarrow{j}-q_{3}\overrightarrow{k}..................................................(4-4)
```
`$ \overrightarrow{q}^{'} $`为`$ \overrightarrow{q} $`的共轭四元数。
**(3)三角式**
```[tex]
\overrightarrow{q} =cos \frac{\theta}{2}+\overrightarrow{u}sin \frac{\theta}{2}..................................................(4-5)
```
`$ \theta $`为实数,`$ \overrightarrow{u} $`为单位向量。
**(4)指数式**
```[tex]
\overrightarrow{q} =e^{\overrightarrow{u}\frac{\theta}{2}}.................................................(4-6)
```
`$ \theta $`为实数,`$ \overrightarrow{u} $`为单位向量。
**(5)矩阵式**
```[tex]
\overrightarrow{q} =\begin{bmatrix}
q_{0}\\
q_{1}\\
q_{2}\\
q_{3}
\end{bmatrix}.................................................(4-7)
```
# 5. 三种表示算法的比较
(1)欧拉角、四元数、旋转矩阵算法比较
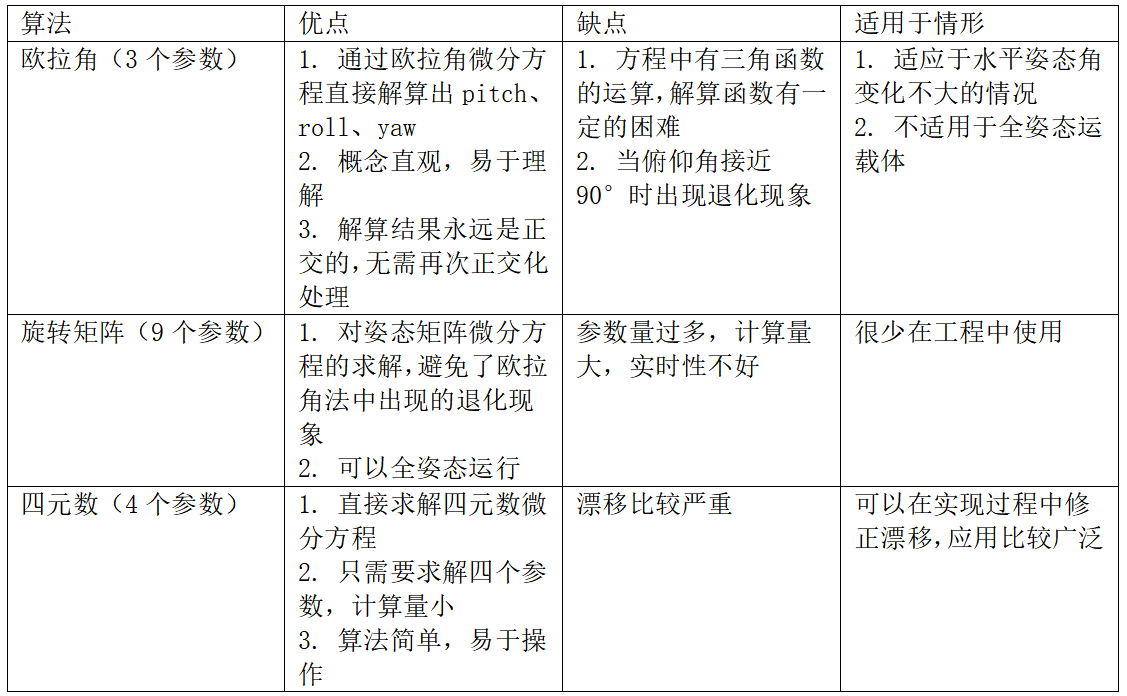
在多旋翼的源码中更多使用的是旋转矩阵和四元数,因为欧拉角存在奇点问题,难用于计算,更多是给人一种直观的表现,,而且欧拉角还存在**旋转万向锁问题**,会导致自由度的缺失,达不到预期效果。而旋转矩阵更多用于两个坐标系之间的转换,姿态表示更多使用的是四元数。
* [旋转万向锁问题视频讲解](https://haokan.baidu.com/v?vid=4922356392425204532&pd=bjh&fr=bjhauthor&type=video)
* [旋转万向锁问题图文讲解,转载>>http://blog.csdn.net/andrewfan](https://www.cnblogs.com/driftingclouds/p/6540222.html)
# 6. 三种表示算法的转换(重点)
欧拉角、旋转矩阵、四元数之间可以相互转换:

# 7. 重规范化
重规范化用来解决使用旋转矩阵,或四元数解算姿态过程中产生的以下两个误差:
**1.积分误差:** 数值积分采用有限时间步长和具有有限采样率的数据。根据所使
用的数值积分方法,对采样的数据做特定的假设。我们所使用的方法假设在每
个时间步长内旋转速度恒定不变。这将引入正比于旋转加速度的误差。
**2.量化误差:** 无论使用哪种方法表示量值,这些表达都是有限的,所以会存在量化误差。从模数转换开始,到执行任何无法保留计算结果所有位数的计算,量化误差都将不断累积。如计算机无法保证其精度而产生的误差。
重规范化思路包括两个过程:归一化和单位化。步骤如下:
**(1)归一化**
两个向量的误差可以使用点乘来计算,如下:
:-: `$ \overrightarrow{X} =\begin{bmatrix}
\overrightarrow{{r_{xx}}}\\
\overrightarrow{r_{xy}}\\
\overrightarrow{r_{xz}}\\
\end{bmatrix} $`,`$ \overrightarrow{Y} =\begin{bmatrix}
\overrightarrow{{r_{yx}}}\\
\overrightarrow{r_{yy}}\\
\overrightarrow{r_{yz}}\\
\end{bmatrix} $`
```[tex]
error=\overrightarrow{X} \cdot \overrightarrow{Y} =\overrightarrow{X}^{T} \cdot \overrightarrow{Y} = \begin{bmatrix}
\overrightarrow{r_{xx}} & \overrightarrow{r_{xy}} & \overrightarrow{r_{xz}}
\end{bmatrix}\begin{bmatrix}
\overrightarrow{r_{yx}} \\
\overrightarrow{r_{yy}} \\
\overrightarrow{r_{yz}}
\end{bmatrix}.................................................(4-7)
```
把误差均分给 X轴 与 Y轴,并近似地将 X轴 与 Y轴分别向相反的方向转动,在此将 X轴 与 Y轴 互相修正,具体操作如下:
```[tex]
\left\{\begin{matrix}
\begin{bmatrix}
\overrightarrow{r_{xx}} \\
\overrightarrow{r_{xy}} \\
\overrightarrow{r_{xz}}
\end{bmatrix}_{orthogonal} = \overrightarrow{X}_{orthogonal} = \overrightarrow{X} - \frac{error}{2} \overrightarrow{Y}\\
\begin{bmatrix}
\overrightarrow{r_{yx}} \\
\overrightarrow{r_{yy}} \\
\overrightarrow{r_{yz}}
\end{bmatrix}_{orthogonal} = \overrightarrow{Y}_{orthogonal} = \overrightarrow{Y} - \frac{error}{2} \overrightarrow{X}
\end{matrix}\right. .................................................(4-8)
```
下一步调整方向余弦的 Z 轴,使得 Z轴 与 X轴 和 Y轴 均正交。这里采用的方法是简单地重新计算 Z轴,使其等于 X轴 与 Y轴的外积。如下:
```[tex]
\begin{bmatrix}
\overrightarrow{r_{zx}} \\
\overrightarrow{r_{zy}} \\
\overrightarrow{r_{zz}}
\end{bmatrix}_{orthogonal} = \overrightarrow{Z}_{orthogonal} = \overrightarrow{X}_{orthogonal} × \overrightarrow{Y}_{orthogonal}.................................................(4-9)
```
**(2)单位化**
单位化是调整方向余弦矩阵每一行的大小使其等于 1。一种方法是:每行的每个元素÷该行元素平方和的二次根。然而有一种更简单的方法,鉴于每行的大小与1相差不大,所以可以采用泰勒展开进行单位化。如下:
```[tex]
\left\{\begin{matrix}
\overrightarrow{X}_{orthogonal} = \frac{1}{2}(3-\overrightarrow{X}_{orthogonal} \cdot \overrightarrow{X}_{orthogonal} ) \overrightarrow{X}_{orthogonal} \\
\overrightarrow{Y}_{orthogonal} = \frac{1}{2}(3-\overrightarrow{Y}_{orthogonal} \cdot \overrightarrow{Y}_{orthogonal} ) \overrightarrow{Y}_{orthogonal} \\
\overrightarrow{Z}_{orthogonal} = \frac{1}{2}(3-\overrightarrow{Z}_{orthogonal} \cdot \overrightarrow{Z}_{orthogonal} ) \overrightarrow{Z}_{orthogonal}
\end{matrix}\right..................................................(4-10)
```
采用该方法单位化的好处是:既没有采用更多的乘法和加法,同时也完全移除了除法与平方根的运算。在每一步积分都执行上述重规范化操作,执行周期为0.02s。如果在代码中发现以**normal**至此重规范化操作完毕。
