四元数的姿态解算就是求解四元数的微分方程:

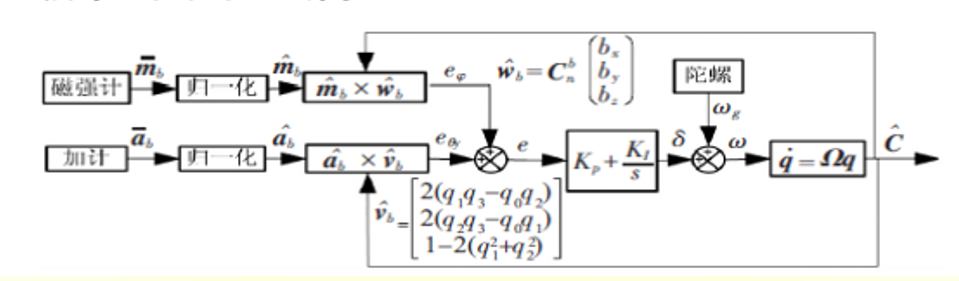
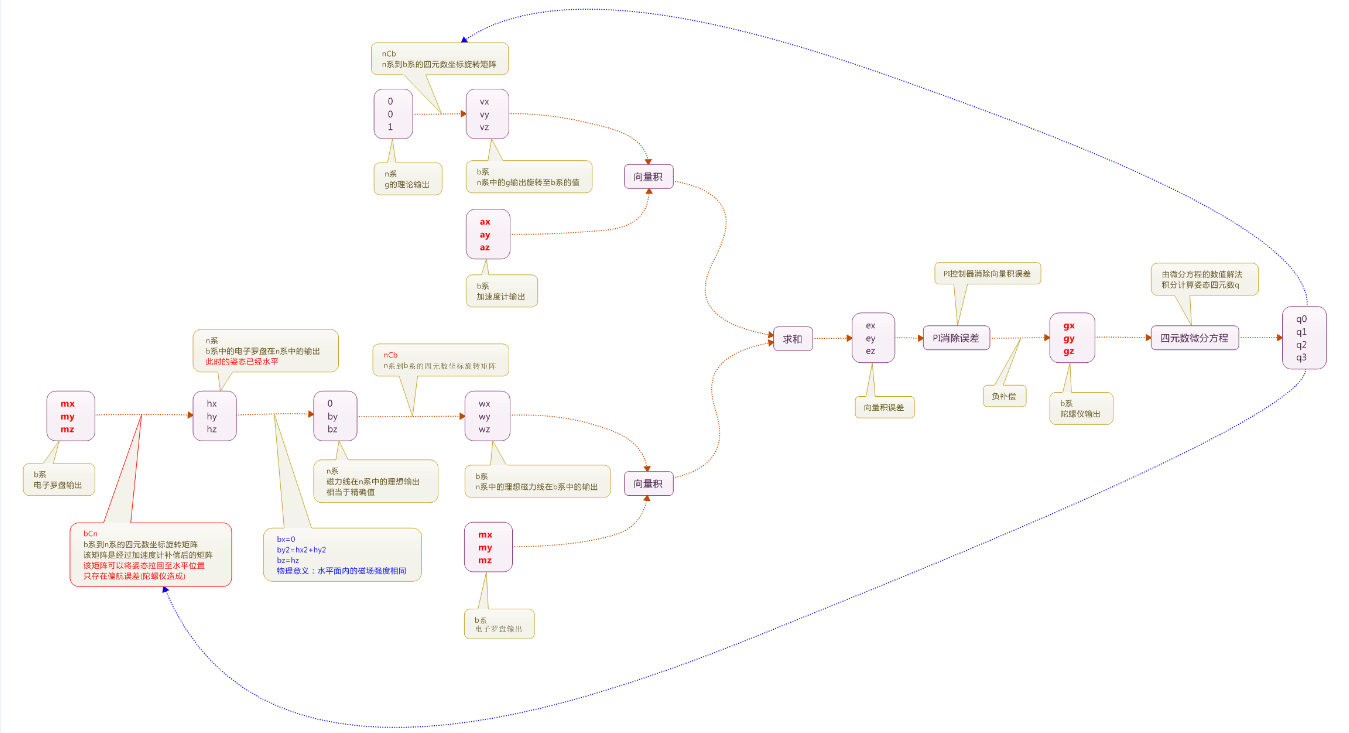
:-: 图 4.2.2-1 四元素姿态解算流程
下面为四元数进行姿态解算的具体步骤:
**1. 初始化四元数**
姿态计算开始,将已知载体的初始姿态角带入式4.2.2-1,求出初始时刻的四元数:
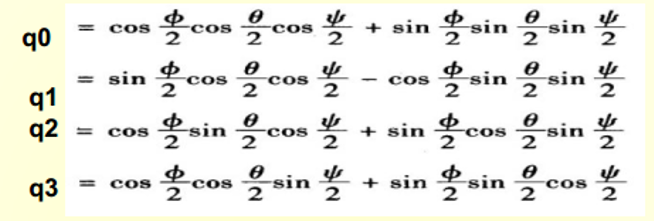-------------(4.2.2-1)
**2. 获取角速度、加速度、磁力计的值**
陀螺仪测量得到的角速度为:`$ [w_x, w_y, w_z] $`,加速度计测量得到的加速度为:`$ [a_x, a_y, a_z] $`,磁力计测量得到的磁场为:`$ [m_x, m_y, m_z] $`。
**3. 将加速度计测量值、磁力计测量值化为单位向量**
**4. 从四元数中获取重力向量和磁场向量**
**(1)通过旋转矩阵乘以加速度计的输出值得到重力向量`$ [\nu_x, \nu_y, \nu_z] $`**

加速度计的实际测量值为`$ [a_x, a_y, a_z] $`,它与重力向量`$ [\nu_x, \nu_y, \nu_z] $`同是表示在 b坐标系下的向量,它们之间的误差按式(4.2.2-3)计算:
```[tex]
[e_x, e_y, e_z] = [\nu_x, \nu_y, \nu_z] × [a_x, a_y, a_z]-------------(4.2.2-3)
```
存在误差的原因是:通过对陀螺仪测得的角速度进行积分获取姿态角时存在的积分误差,从而导致重力向量`$ [\nu_x, \nu_y, \nu_z] $`的不准确。
**(2)通过旋转矩阵乘以磁力计的输出值得到磁场向量**
磁力线由北指向南,近乎垂直于地球表面。由于Y轴与磁力线垂直,所以在Y轴上的磁场为 0 ,地球磁场就为:`$ [b_x, 0, b_z] $`,但是这个磁场向量有时是未知的,所以需要经过以下两个步骤才能得到准确角速度值。
1)求出磁场向量
-----------------------------(4.2.2-X)
2)求出角速度
磁力计在XOY平面上(n系)的向量大小必定相同,令`$ b_x = \sqrt{h_{x}^{2} + h_{x}^{2}},b_z = h_z,b_y = 0 $`,然后通过式(4.2.2-X1)求出角速度:
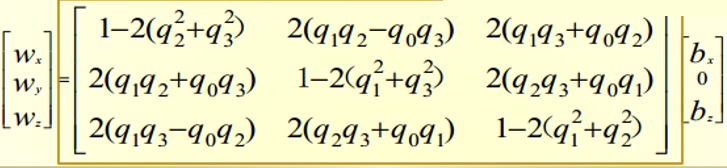-----------------------------(4.2.2-X1)
误差为:
```[tex]
[e_x, e_y, e_z] = [m_x, m_y, m_z] × [w_x, w_y, w_z]-------------(4.2.2-3a)
```
**5. 计算误差**
-----------------------------(4.2.2-X)
**6. 利用误差修正陀螺仪**
使用PI算法来修改误差:
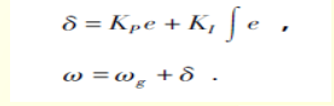-----------------------------(4.2.2-4)
`$ K_{p} $`比例系数,`$ e $`误差,`$ K_{i} $`积分系数,`$ w $`为修正后的陀螺仪数据(角速度)。
**7. 利用修正后的陀螺仪数值更新四元数**
利用一阶龙格—库塔法求解微分方程,一阶龙格—库塔法表达式如式(4.2.2-5)
```[tex]
\dot{x} = f[x(t), w(t)]x(t+T) = x(t) + Tf[x(t), w(t)]---------(4.2.2-5)
```
四元数更新如式(4.2.2-6):
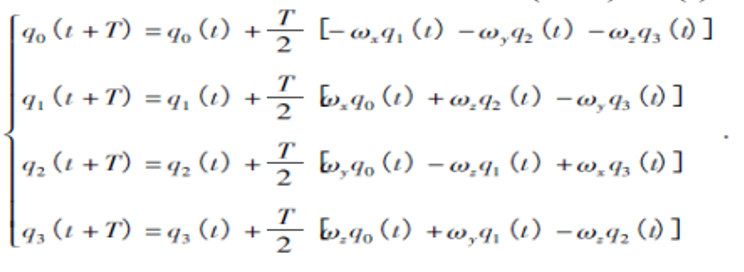------------(4.2.2-6)
第**4**步到第**7**步需要不断地迭代,直到满足为止。
**8. 将更新后的四元素规范化**
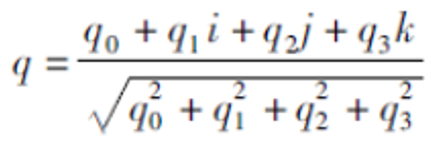---------(4.2.2-7)
**9. 将四元数转换为欧拉角**
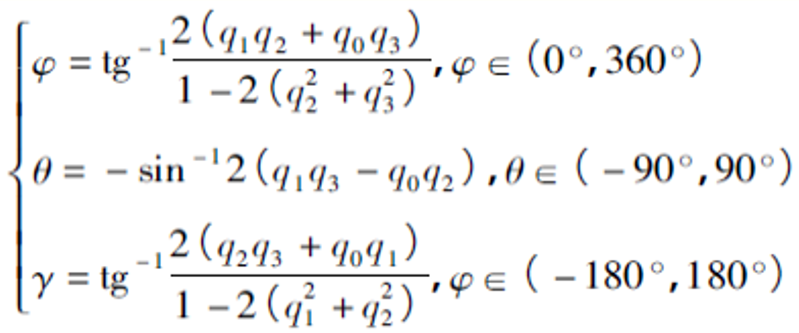---------(4.2.2-8)
至此,四元数的姿态解算就完成了。下图表示四元素姿态的解算流程。