# 四、图嵌入技术
在本节中,我们基于所使用的技术对图嵌入方法进行分类。 通常,图嵌入旨在在低维空间中表示图,保留尽可能多的图属性信息。 不同图嵌入算法之间的区别在于,它们如何定义要保留的图属性。 不同的算法对节点(边、子结构、整图)的相似性,以及如何在嵌入空间中保留它们,有不同的见解。 接下来,我们将介绍每种图嵌入技术的见解,以及它们如何量化图属性并解决图嵌入问题。
## 矩阵分解
基于矩阵分解的图嵌入,以矩阵的形式表示图特性(例如,节点成对相似性)并对该矩阵进行分解来获得节点嵌入[11]。 图嵌入的开创性研究通常以这种方式解决图嵌入问题。 在大多数情况下,输入是由非关系高维数据特征构成的图,如第 3.1.4 节中所介绍的。输出是一组节点嵌入(Sec.3.2.1)。 因此,图嵌入的问题可以被视为保持结构的降维问题,其假定输入数据位于低维流形中。 有两种类型的基于矩阵分解的图嵌入。 一种是分解图的拉普拉斯特征映射 ,另一种是直接分解节点邻近矩阵 。
### 图的拉普拉斯算子
见解: 要保留的图属性可以解释为成对节点的相似性。 因此,如果两个具有较大相似性的节点相距很远,则会施加较大的惩罚。
**表4:**基于图的拉普拉斯特征映射的图嵌入。
| GE算法 |  | 目标函数 |
| --- | --- | --- |
| MDS [74] | 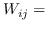 欧氏距离 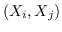 | 公式 2 |
| Isomap [78] | KNN, 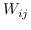 是沿着 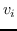 到 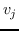 最短路径的边权重之和 | 公式 2 |
| LE [96] | KNN, 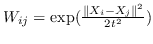 | 公式 2 |
| LPP [97] | KNN, 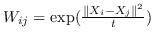 | 公式 4 |
| AgLPP [79] | 锚图, 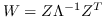 , 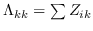 , 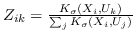 | 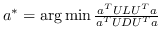 |
| LGRM [98] | KNN, 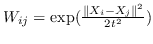 | 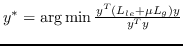 |
| ARE [88] | KNN, 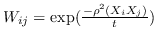 , 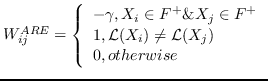 | `<6244>` |
| SR [99] | KNN, 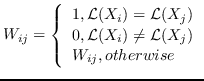 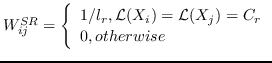 | `<6248>` |
| HSL [87] | 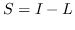 ,其中 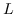 是归一化的超图的拉普拉斯算子 | 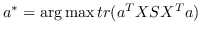 ,圣 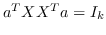 |
| MVU [100] | KNN, 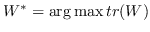 ,圣 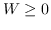 , 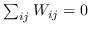 和 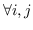 , | `<6255>` |
| SLE [86] | KNN, 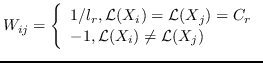 | `<6259>` |
| MSHLRR [76] | 一般图:KNN, 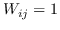 | 公式 2 |
| | 超图: 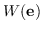 是一个夸张的重量 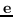 |
| | 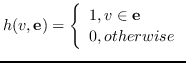 , 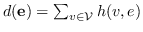 |
| [77] |  | 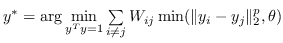 |
| PUFS [75] | KNN, 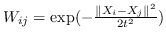 | 公式 4 +(must 和 cannot 链接约束) |
| RF-Semi-NMF-PCA [101] | KNN, 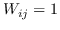 | 公式 2 + 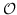 (PCA)+ 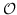 (k均值) |
基于以上见解,最优的嵌入 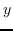 可以由以下目标函数[99]导出。
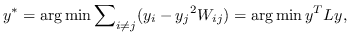 (1)
其中 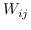 是节点 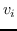 和 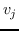 之间的“定义的”相似性;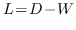 是图的拉普拉斯。  是对角矩阵,其中 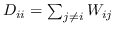。 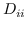 的值越大,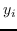 就更重要[97]。 约束 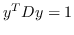 通常加于 Eq.1,来删除嵌入中的任意缩放因子。 Eq.1 然后化简为:
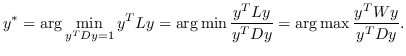 (2)
最优的 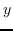 是特征问题 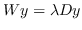 的最大特征值对应的特征向量。
上面的图嵌入是渐进式的,因为它只能嵌入训练集中存在的节点。 在实践中,它可能还需要嵌入未在训练中看到的新节点。 一种解决方案是设计线性函数 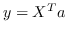 这样只要提供了节点特征,就可以导出嵌入。 因此,对于归纳性的图嵌入,Eq.1 变为在以下目标函数中找到最的 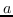:
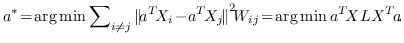 (3)
与 Eq.2 相似,通过添加约束 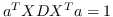 ,公式 3 中的问题变成:
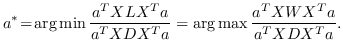 (4)
最优的 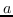 是 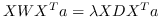 的解的最大特征值的特征向量。
现有研究的差异主要在于它们如何计算成对节点的相似性  ,以及它们是否使用线性函数 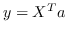 或不。 已经进行了一些尝试[85,81]以使用一般框架总结现有的基于拉普拉斯特征图的图嵌入方法。 但他们的综述只涵盖了有限的工作量。 在表 4 中 ,我们总结了现有的基于拉普拉斯特征图的图嵌入研究,并比较了它们的 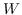 的计算方法,以及他们采用了什么样的目标函数。
最初的研究 MDS [74]直接采用了两个特征向量 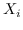 和 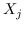 之间的欧几里德距离,作为 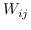。公式 2 用于找到 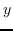 的最佳嵌入。 MDS不考虑节点的邻域,即,任何一对训练实例都被认为是连接的。 后续研究(例如,[78,102,96,97])通过首先从数据特征构建 k 最近邻(KNN)图来克服该问题。 每个节点仅与其前 k 个相似的邻居连接。 之后,利用不同的方法来计算相似度矩阵 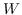,以便尽可能多地保留所需的图属性。 最近设计了一些更高级的模型。 例如,AgLPP [79]引入了锚图,显着提高早期矩阵分解模型 LPP 的效率。 LGRM [98]学习局部回归模型来掌握图结构,和样本外数据外插值的全局回归项。 最后,与以前的工作保留局部几何不同,LSE [103]使用局部样条回归来保持全局几何。
当辅助信息(例如,标签,属性)可用时,调整目标函数以保留更丰富的信息。 例如,[99]构造邻接图 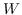 和标记图 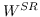。 目标函数由两部分组成,一部分侧重于保留数据集的局部几何结构,如LPP [97],另一部分试图在标记的训练数据上获得具有最佳类的可分性的嵌入。 类似地,[88]也构造了两个图,即邻接图 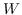 编码局部几何结构,反馈关系图 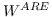 编码用户相关反馈中的成对关系。 RF-Semi-NMF-PCA [101]通过构建由三个部分组成的目标函数:PCA,k-means和图的拉普拉斯正则化,同时考虑聚类,降维和图嵌入。
其他一些工作认为 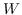 不能通过容易枚举成对节点关系来构造。 相反,他们采用半定规划(SDP)来学习 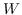 。 具体而言,SDP [104]的目的是找到一个内积矩阵,它最大化在图中没有连接的任何两个输入之间的成对距离,同时保留最近的邻居距离。 MVU [100]构造这样的矩阵,然后在习得的内积矩阵上应用MDS [74]。 [2]证明正则化LPP [97]相当于正则化SR [99],如果 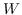 是对称的,双随机的,PSD并且秩为 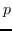 。 它构造了这种相似矩阵,从而有效地解决了类似LPP的问题。
**表5:**基于节点邻近矩阵分解的图嵌入。`O(*)`表示目标函数;例如,`O(SVM分类器)`表示SVM分类器的目标函数。
| GE算法 | 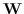 | 目标函数 |
| --- | --- | --- |
| [50] | 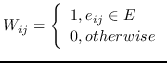 | 公式 5 |
| SPE [105] | KNN, 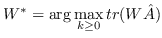 ,约束为 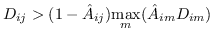 | 公式 5 |
| HOPE [106] | Katz 指数 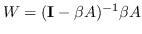 ; 个性化的 Pagerank 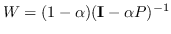 | 公式 5 |
| GraRep [21] | 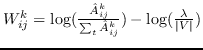 ,其中 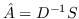 , 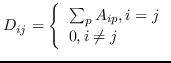 | 公式 5 |
| CMF [43] | PPMI | 公式 5 |
| TADW [56] | PMI | 公式 5 和文本特征矩阵 |
| [24] | `A` | 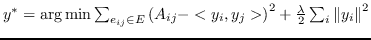 |
| MMDW [48] | PMI | 公式 5 + `O(SVM分类器)` |
| HSCA [57] | PMI | `O(MMDW)`+( 一阶邻近度约束) |
| MVE [107] | KNN, 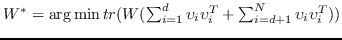 | 公式 5 |
| M-NMF [1] | 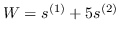 | 公式 5 + `O(社区检测)` |
| ULGE [2] | 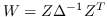 ,其中 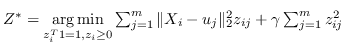 | 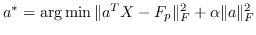 |
| LLE [102] | KNN, 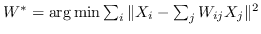 | 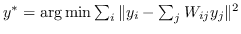 |
| RESCAL [108] | 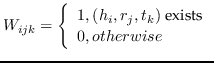 | 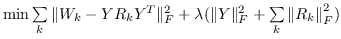 |
| FONPE [109] | KNN, 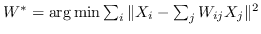 | 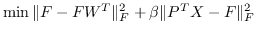 ,约束为 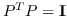 |
### 节点邻近矩阵分解
除了解决上述广义特征值问题外,另一系列研究试图直接分解节点邻近矩阵。
见解: 使用矩阵分解可以在低维空间中近似节点邻近度。 保持节点邻近度的目标是最小化近似的损失。
给定节点邻近矩阵 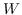 ,目标是:
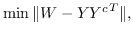 (5)
其中 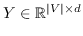 是节点嵌入,和 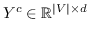 是上下文节点的嵌入[21]。
公式 5 旨在找到一个最优的秩为`d`的邻近度矩阵`W`的近似( 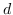 是嵌入的维度)。 一种流行的解决方案是对 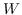 应用 SVD(奇异值分解)[110]。从形式上看,
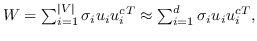 (6)
其中 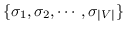 是按降序排序的奇异值, 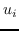 和 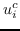 是 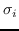 的奇异向量 。 最佳嵌入使用最大的`d`个奇异值获得 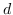,相应的奇异向量如下:
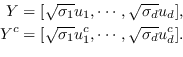 (7)
根据是否保留非对称属性,节点 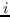 的嵌入是 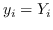 [21,50],或 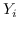 和 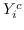 连接,即 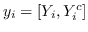 [106]。 公式 5 存在其他解决方案,如正则化高斯矩阵分解[24],低秩矩阵分解[56],并加入其他正则化器来施加更多约束[48]。 我们总结了表 5 中所有基于节点邻近度矩阵分解的图嵌入。
总结:矩阵分解(MF)主要用于嵌入由非关系数据构建的图(第 3.1.4 节),用于节点嵌入(第 3.2.1 节),这是图的拉普拉斯特征映射问题的典型设定。 MF也用于嵌入同构图[50,24](第 3.1.1 节)。
## 深度学习
深度学习(DL)在各种研究领域表现出色,如计算机视觉,语言建模等。基于DL的图嵌入在图上应用DL模型。 这些模型要么直接来自其他领域,要么是专门为嵌入图数据设计的新神经网络模型。 输入是从图中采样的路径或整个图本身。 因此,我们基于是否采用随机游走来从图中采样路径,将基于DL的图嵌入分为两类。
### 带有随机游走的基于 DL 的图嵌入
见解: 通过最大化以自身嵌入为条件的,节点邻域的观测概率,可以在嵌入空间中保留图中的二阶邻近度。
在第一类基于深度学习的图嵌入中,图被表示为从其采样的一组随机游走路径。 然后将深度学习方法应用于用于图嵌入的采样路径,保留路径所承载的图属性。
鉴于上述见解,DeepWalk [17]采用神经语言模型(SkipGram)进行图嵌入。 SkipGram [111]旨在最大化窗口内出现的单词之间的共现概率 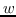 。 DeepWalk首先使用截断的随机游走,从输入图中采样一组路径(即,均匀地采样最后访问节点的邻居,直到达到最大长度)。 从图中采样的每个路径相当于来自语料库的句子,其中节点相当于单词。 然后将SkipGram应用于路径,最大化节点邻域的观测概率,以自身嵌入为条件。 以这种方式,邻域相似(二阶邻近度较大)的节点的嵌入相似。DeepWalk的目标函数如下:
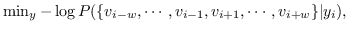 (8)
其中 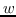 是窗口大小,它限制随机游走上下文的大小。 SkipGram删除了排序约束,并且 公式 8转换为:
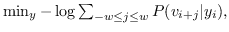 (9)
其中 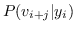 使用softmax函数定义:
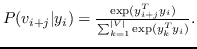 (10)
请注意,计算公式 10 是昂贵的,因为标准化因子(即,图中每个节点的所有内积的总和),所以图 10 的方法是不可行的。 通常有两种解近似完全softmax的解决方案:分层softmax [112]和负采样[112]。
分层softmax :有为了效地解决中公式 10,构造二叉树,其中节点被分配给叶子。 不像公式 10 那样枚举所有节点,仅需要求解从根到相应叶子的路径。 优化问题变得最大化树中特定路径的概率。 假设到叶子 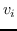 的路径是一系列节点 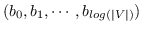 ,其中`b0`为根, 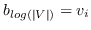 。 公式 10 然后变成:
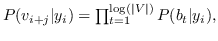 (11)
其中 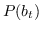 是二分类器: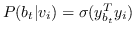。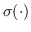 表示 S 形函数。 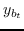 是树节点 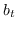 的父节点的嵌入 。 分层softmax减少了SkipGram的时间复杂度,从 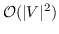 至 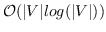。
负采样 : 负采样的关键思想是,使用逻辑回归将目标节点与噪声区分开来。 即,对于一个节点 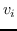 ,我们想区分它的邻居 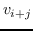 来自其他节点。 噪音分布 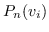 用于绘制节点的负样本 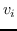 。公式 9 中的每个 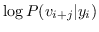 然后计算为:
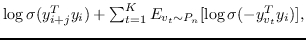 (12)
其中 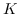 是采样的负节点数。 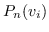 是一种噪声分布,例如均匀分布(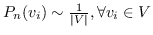)。 具有负采样的SkipGram的时间复杂度是 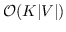。
**表6:**带有随机游走路径的基于深度学习的图嵌入。
| GE算法 | 随机游走方法 | 保留的邻近度 | DL模型 |
| --- | --- | --- | --- |
| DeepWalk [17] | 截断随机游走 | 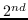 | SkipGram 和 分层 softmax(公式 11) |
| [34] | 截断随机游走 | 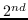 (词语-图像) | 同上 |
| GenVector [66] | 截断随机游走 | 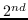 (用户 - 用户和概念 - 概念) | 同上 |
| 受限制的DeepWalk [25] | 边权重采样 | 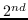 | 同上 |
| DDRW [47] | 截断随机游走 | 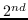 +分类一致性 | 同上 |
| TriDNR [73] | 截断随机游走 | 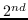 (节点,单词和标签之间) | 同上 |
| node2vec [28] | BFS + DFS | 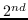 | SkipGram 和负采样(公式 12) |
| UPP-SNE [113] | 截断随机游走 | 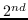 (用户 - 用户和个人资料 - 个人资料) | 同上 |
| Planetoid [62] | 按标签和结构对节点对进行采样 | 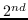 +标签标识 | 同上 |
| NBNE [19] | 对节点的直接邻居进行采样 | 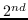 | 同上 |
| DGK [93] | graphlet 核:随机采样[114] | 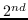 (通过graphlet) | SkipGram(公式11 - 12 ) |
| metapath2vec [46] | 基于元路径的随机游走 | 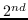 | 异构 SkipGram |
| ProxEmbed [44] | 截断随机游走 | 节点排名元组 | LSTM |
| HSNL [29] | 截断随机游走 | 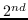 + QA排名元组 | LSTM |
| RMNL [30] | 截断随机游走 | 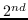 +用户问题质量排名 | LSTM |
| DeepCas [63] | 基于马尔可夫链的随机游走 | 信息级联序列 | GRU |
| MRW-MN [36] | 截断随机游走 | 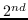 +跨模态特征差异 | DCNN + SkipGram |
DeepWalk [17]的成功激发了许多后续研究,这些研究将深度学习模型(例如,SkipGram或长短期记忆(LSTM)[115])应用于图嵌入的采样路径。 我们在表 6中对它们进行了总结。 如表中所示,大多数研究遵循DeepWalk的想法,但改变随机游戏的采样方法([25,28,62,62])或要保留的邻近度(定义 5和定义 6)的设定([34,66,47,73,62])。 [46]设计基于元路径的随机游走来处理异构图和异构 SkipGram,它最大化了给定节点具有异构上下文的概率。 除了SkipGram之外,LSTM是图嵌入中采用的另一种流行的深度学习模型。 请注意,SkipGram只能嵌入一个节点。 然而,有时我们可能需要将一系列节点嵌入为固定长度向量,例如,将句子(即,一系列单词)表示为一个向量,就要在这种情况下采用LSTM来嵌入节点序列。 例如,[29]和[30]嵌入cQA站点中的问题/答案中的句子,[44]在两个节点之间嵌入一系列节点,用于邻近度嵌入。 在这些工作中优化排名损失函数,来保持训练数据中的排名分数。 在[63]中,GRU [116](即,类似于LSTM的递归神经网络模型)用于嵌入信息级联路径。
#### 不带随机游走的基于 DL 的图嵌入
见解: 多层学习架构是一种强大而有效的解决方案,可将图编码为低维空间。
第二类基于深度学习的图嵌入方法直接在整个图(或整个图的邻近矩阵)上应用深度模型。 以下是图嵌入中使用的一些流行的深度学习模型。
自编码器 :自编码器旨在最小化其编码器输入和解码器输出的重建误差。 编码器和解码器都包含多个非线性函数。 编码器将输入数据映射到表示空间,并且解码器将表示空间映射到重建空间。 采用自编码器进行图嵌入的思想,与邻域保持方面的节点邻近矩阵分解(Sec.4.1.2)相似。 具体而言,邻接矩阵捕获节点的邻域。 如果我们将邻接矩阵输入到自编码器,则重建过程将使具有相似邻域的节点具有类似的嵌入。
深度神经网络 :作为一种流行的深度学习模型,卷积神经网络(CNN)及其变体已广泛应用于图嵌入。 一方面,他们中的一些人直接使用为欧几里德域设计的原始CNN模型,并重新格式化输入图以适应它。 例如,[55]使用图标记,从图中选择固定长度的节点序列,然后使用 CNN 模型,组装节点的邻域来学习邻域表示。 另一方面,一些其他工作试图将深度神经模型推广到非欧几里德域(例如,图)。 [117]在他们的综述中总结了代表性研究。 通常,这些方法之间的差异在于,它们在图上形成类似卷积的操作的方公式 一种方法是模拟卷积定理以定义谱域中的卷积 [118,119]。 另一种方法是将卷积视为空域中的邻域匹配 [82,72,120]。
其他 :还有一些其他类型的基于深度学习的图嵌入方法。 例如,[35]提出了DUIF,它使用分层softmax作为前向传播来最大化模块性。 HNE [33]利用深度学习技术来捕获异构成分之间的交互,例如,用于图像的CNN和用于文本的FC层。 ProjE [40]设计了一个具有组合层和投影层的神经网络。 它定义了知识图嵌入的逐点损失(类似于多分类)和列表损失(即softmax回归损失)。
我们在表 7 中总结了所有基于深度学习的图嵌入方法(没有随机游走),并比较了它们使用的模型以及每个模型的输入。
**表7:**基于深度学习的图嵌入, 没有随机游走路径。
| GE 算法 | 深度学习模型 | 模型输入 |
| --- | --- | --- |
| SDNE [20] | 自编码器 | 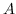 |
| DNGR [23] | 堆叠去噪自编码器 | PPMI |
| SAE [22] | 稀疏自编码器 | 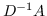 |
| [55] | CNN | 节点序列 |
| SCNN [118] | 谱 CNN | 图 |
| [119] | 带有光滑谱乘法器的谱 CNN | 图 |
| MoNet [80] | 混合模型网络 | 图 |
| ChebNet [82] | 图CNN又名ChebNet | 图 |
| GCN [72] | 图卷积网络 | 图 |
| GNN [120] | 图神经网络 | 图 |
| [121] | 自适应图神经网络 | 分子图 |
| GGS-NNs [122] | 自适应图神经网络 | 图 |
| HNE [33] | CNN + FC | 带图像和文本的图 |
| DUIF [35] | 分层深度模型 | 社会管理网络 |
| ProjE [40] | 神经网络模型 | 知识图 |
| TIGraNet [123] | 图卷积网络 | 从图像构造的图 |
总结:由于它的威力和效率,深度学习已广泛应用于图嵌入。 在基于深度学习的图嵌入方法中,已经观察到三种类型的输入图(除了从非关系数据构建的图(第 3.1.4 节))和所有四种类型的嵌入输出。
- TensorFlow 1.x 深度学习秘籍
- 零、前言
- 一、TensorFlow 简介
- 二、回归
- 三、神经网络:感知器
- 四、卷积神经网络
- 五、高级卷积神经网络
- 六、循环神经网络
- 七、无监督学习
- 八、自编码器
- 九、强化学习
- 十、移动计算
- 十一、生成模型和 CapsNet
- 十二、分布式 TensorFlow 和云深度学习
- 十三、AutoML 和学习如何学习(元学习)
- 十四、TensorFlow 处理单元
- 使用 TensorFlow 构建机器学习项目中文版
- 一、探索和转换数据
- 二、聚类
- 三、线性回归
- 四、逻辑回归
- 五、简单的前馈神经网络
- 六、卷积神经网络
- 七、循环神经网络和 LSTM
- 八、深度神经网络
- 九、大规模运行模型 -- GPU 和服务
- 十、库安装和其他提示
- TensorFlow 深度学习中文第二版
- 一、人工神经网络
- 二、TensorFlow v1.6 的新功能是什么?
- 三、实现前馈神经网络
- 四、CNN 实战
- 五、使用 TensorFlow 实现自编码器
- 六、RNN 和梯度消失或爆炸问题
- 七、TensorFlow GPU 配置
- 八、TFLearn
- 九、使用协同过滤的电影推荐
- 十、OpenAI Gym
- TensorFlow 深度学习实战指南中文版
- 一、入门
- 二、深度神经网络
- 三、卷积神经网络
- 四、循环神经网络介绍
- 五、总结
- 精通 TensorFlow 1.x
- 一、TensorFlow 101
- 二、TensorFlow 的高级库
- 三、Keras 101
- 四、TensorFlow 中的经典机器学习
- 五、TensorFlow 和 Keras 中的神经网络和 MLP
- 六、TensorFlow 和 Keras 中的 RNN
- 七、TensorFlow 和 Keras 中的用于时间序列数据的 RNN
- 八、TensorFlow 和 Keras 中的用于文本数据的 RNN
- 九、TensorFlow 和 Keras 中的 CNN
- 十、TensorFlow 和 Keras 中的自编码器
- 十一、TF 服务:生产中的 TensorFlow 模型
- 十二、迁移学习和预训练模型
- 十三、深度强化学习
- 十四、生成对抗网络
- 十五、TensorFlow 集群的分布式模型
- 十六、移动和嵌入式平台上的 TensorFlow 模型
- 十七、R 中的 TensorFlow 和 Keras
- 十八、调试 TensorFlow 模型
- 十九、张量处理单元
- TensorFlow 机器学习秘籍中文第二版
- 一、TensorFlow 入门
- 二、TensorFlow 的方式
- 三、线性回归
- 四、支持向量机
- 五、最近邻方法
- 六、神经网络
- 七、自然语言处理
- 八、卷积神经网络
- 九、循环神经网络
- 十、将 TensorFlow 投入生产
- 十一、更多 TensorFlow
- 与 TensorFlow 的初次接触
- 前言
- 1. TensorFlow 基础知识
- 2. TensorFlow 中的线性回归
- 3. TensorFlow 中的聚类
- 4. TensorFlow 中的单层神经网络
- 5. TensorFlow 中的多层神经网络
- 6. 并行
- 后记
- TensorFlow 学习指南
- 一、基础
- 二、线性模型
- 三、学习
- 四、分布式
- TensorFlow Rager 教程
- 一、如何使用 TensorFlow Eager 构建简单的神经网络
- 二、在 Eager 模式中使用指标
- 三、如何保存和恢复训练模型
- 四、文本序列到 TFRecords
- 五、如何将原始图片数据转换为 TFRecords
- 六、如何使用 TensorFlow Eager 从 TFRecords 批量读取数据
- 七、使用 TensorFlow Eager 构建用于情感识别的卷积神经网络(CNN)
- 八、用于 TensorFlow Eager 序列分类的动态循坏神经网络
- 九、用于 TensorFlow Eager 时间序列回归的递归神经网络
- TensorFlow 高效编程
- 图嵌入综述:问题,技术与应用
- 一、引言
- 三、图嵌入的问题设定
- 四、图嵌入技术
- 基于边重构的优化问题
- 应用
- 基于深度学习的推荐系统:综述和新视角
- 引言
- 基于深度学习的推荐:最先进的技术
- 基于卷积神经网络的推荐
- 关于卷积神经网络我们理解了什么
- 第1章概论
- 第2章多层网络
- 2.1.4生成对抗网络
- 2.2.1最近ConvNets演变中的关键架构
- 2.2.2走向ConvNet不变性
- 2.3时空卷积网络
- 第3章了解ConvNets构建块
- 3.2整改
- 3.3规范化
- 3.4汇集
- 第四章现状
- 4.2打开问题
- 参考
- 机器学习超级复习笔记
- Python 迁移学习实用指南
- 零、前言
- 一、机器学习基础
- 二、深度学习基础
- 三、了解深度学习架构
- 四、迁移学习基础
- 五、释放迁移学习的力量
- 六、图像识别与分类
- 七、文本文件分类
- 八、音频事件识别与分类
- 九、DeepDream
- 十、自动图像字幕生成器
- 十一、图像着色
- 面向计算机视觉的深度学习
- 零、前言
- 一、入门
- 二、图像分类
- 三、图像检索
- 四、对象检测
- 五、语义分割
- 六、相似性学习
- 七、图像字幕
- 八、生成模型
- 九、视频分类
- 十、部署
- 深度学习快速参考
- 零、前言
- 一、深度学习的基础
- 二、使用深度学习解决回归问题
- 三、使用 TensorBoard 监控网络训练
- 四、使用深度学习解决二分类问题
- 五、使用 Keras 解决多分类问题
- 六、超参数优化
- 七、从头开始训练 CNN
- 八、将预训练的 CNN 用于迁移学习
- 九、从头开始训练 RNN
- 十、使用词嵌入从头开始训练 LSTM
- 十一、训练 Seq2Seq 模型
- 十二、深度强化学习
- 十三、生成对抗网络
- TensorFlow 2.0 快速入门指南
- 零、前言
- 第 1 部分:TensorFlow 2.00 Alpha 简介
- 一、TensorFlow 2 简介
- 二、Keras:TensorFlow 2 的高级 API
- 三、TensorFlow 2 和 ANN 技术
- 第 2 部分:TensorFlow 2.00 Alpha 中的监督和无监督学习
- 四、TensorFlow 2 和监督机器学习
- 五、TensorFlow 2 和无监督学习
- 第 3 部分:TensorFlow 2.00 Alpha 的神经网络应用
- 六、使用 TensorFlow 2 识别图像
- 七、TensorFlow 2 和神经风格迁移
- 八、TensorFlow 2 和循环神经网络
- 九、TensorFlow 估计器和 TensorFlow HUB
- 十、从 tf1.12 转换为 tf2
- TensorFlow 入门
- 零、前言
- 一、TensorFlow 基本概念
- 二、TensorFlow 数学运算
- 三、机器学习入门
- 四、神经网络简介
- 五、深度学习
- 六、TensorFlow GPU 编程和服务
- TensorFlow 卷积神经网络实用指南
- 零、前言
- 一、TensorFlow 的设置和介绍
- 二、深度学习和卷积神经网络
- 三、TensorFlow 中的图像分类
- 四、目标检测与分割
- 五、VGG,Inception,ResNet 和 MobileNets
- 六、自编码器,变分自编码器和生成对抗网络
- 七、迁移学习
- 八、机器学习最佳实践和故障排除
- 九、大规模训练
- 十、参考文献
