>[success] # 最坏/最好时间复杂度 [下面内容是通过极客时间整理得到的](https://time.geekbang.org/column/article/40447) ~~~ 1.下面的代码是要做，通过n来控制循环多少项，来找到x所在'array'的位 置，利用之前的分析方法，首先直接看运行次数最多的语句,循环句中 控住'数据的规模的大小'n，则整体的运行时间为：T(n) = O(n),这里要说明 这里没有break 即使找到了也要循环全部才算完事，且这里考虑的情况n是 数组长度 ~~~ ~~~ function test(array, n,x){ let i = 0 let pos = -1 for(;i<n;i++){ if(array[i] === x) pos = i } return pos } ~~~ >[danger] ##### 改造上面代码再分析（最好/最坏） ~~~ 1.将代码中加入了break后整个影响整段代码运行时间不在单单是'n'这个数据 规模，还有一个就是'x'所在位置，x所在位置最优的肯定是在第一位那么复 杂度O(1),最坏的时间复杂度x在整个数组最后一项O(n) ~~~ ~~~ function test(array, n,x){ let i = 0 let pos = -1 for(;i<n;i++){ if(array[i] === x) { pos = i break } } return pos } ~~~ >[success] # 平均时间复杂度 ~~~ 1.刚才分析了最坏/最好的时间复杂度，但代码不可能都是这种极端的情况 ，即最好最坏因此出来了平均时间复杂度概念 2.来分析数组如果是 array = [1,2], 不考虑'n'为0 则也就是一次都不循环的情 况，如果'x'为1 也就是代码循环一次即找到位置，'x'为2即代码循环两次找到 位置，那么他的平均时间则为 (1+2)/2 = 1.5,即得到下面公式 ~~~ * 其中n+1为数组长度（因为数组是从0开始计数，因此长度需要加1），分子为出现的情况总和  ~~~ 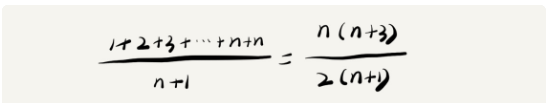1.得到上面公式后，再根据之前学的法则，时间复杂度的大 O 标记法中，可 以省略掉系数、低阶、常量，所以，咱们把刚刚这个公式简化之后，得到的 平均时间复杂度就是 O(n)。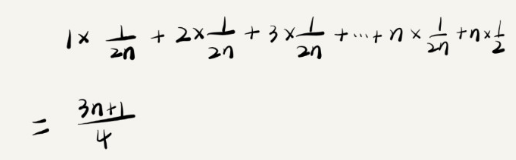 ~~~ * 考虑概率 ~~~ 1.实际考虑概率即'x'存在数组和不存在数组这两种情况，得到的公式如图 2.则遵循法则得到O(n) ~~~  >[success] # 均摊时间复杂度 ~~~ 1.下面的代码只有在最特殊的情况下也就是 count 等于array.length时候，他 的复杂度才为O(n),在这之前的复杂度都为O(1) 2.最理想情况下**x!=n**，只执行一次赋值即可推出，所以最好时间复杂度为O(1)。 最坏的情况下**x=n**，要执行一次循环累加和的操作，所以最好时间复杂度为O(n)。 平均的情况下，因为限定条件0<=x<=n，x在0~n中存在的位置可以分为n+1种情况(0到n)。 当**0<=x<n**时，时间复杂度为O(1)。但是**x=n**的时候是一个例外，它的复杂度是O(n)。 而且这n+1种情况发生的概率都是一样的，为**1n+11n+1。**所以根据加权平均的计算方法， ~~~ * [图片出处](https://www.cnblogs.com/jonins/p/9956752.html)，简单的说除非当count等于数组长度否则其余复杂度都为1，也正是如此在数组最后一项之前出现的复杂度都为1他们出现的概率为1/n+1,了解清楚后就会得到下面的公式1为复杂度1/n+1 为改复杂度出现的概率当省略系数及常量后，平均时间复杂度为O(1)，也就是当把复杂度最高的情况n*(1/n+1)摊还其他 1的情况下最后忽略看成O(1)  ~~~ // array 表示一个长度为 n 的数组 // 代码中的 array.length 就等于 n int[] array = new int[n]; int count = 0; void insert(int val) { if (count == array.length) { int sum = 0; for (int i = 0; i < array.length; ++i) { sum = sum + array[i]; } array[0] = sum; count = 1; } array[count] = val; ++count; } ~~~ >[success] # 总结平均和均摊 ~~~ 1.平均就是在连续没有规律的情况下使用平均，即可理解当使用find 方法的 时候，是要找的项在每一项不同情况他的运行时间是不一定，即这种情况需要平均即为O(n) 2.均摊当add （js的push）时候只为末尾添加一项，即非要需要的添加项实际无需做处理即为O(1),到达最后一项我们这里是抽象的把push想成到最后 一项去循环所有数组并且添加一项此时为O(n),均摊则为O(1) ~~~